Fourier Transformation
Die Fourier-Transformation ist das Verfahren zur Bestimmung der Fourier-Transformierten. Diese spielt eine wesentliche Rolle bei der Zerlegung einer nicht-periodischen Ausgangsfunktion in trigonometrische Funktionen mit unterschiedlichen Frequenzen. Die Fourier-Transformierte beschreibt das sogenannte Frequenzspektrum, d.h. sie ordnet jeder Frequenz die passende Amplitude für die gesuchte Zerlegung zu.
In diesem Artikel zeigen wir dir anhand von einem Beispiel, wie die Fourier Transformation funktioniert und gehen auf die Anwendung ein. Am Ende zeigen wir dir noch einmal eine übersichtliche Tabelle zur Fourier Transformation. Die wichtigsten Punkte sind auch in unserem Video zusammengefasst. Schau rein!
Inhaltsübersicht
Fourier Transformation einfach erklärt
In der Fourier Analyse ist das allgemeine Ziel, eine gegebene Funktion  als Linearkombination der periodischen Sinus- und Cosinus-Funktionen zu beschreiben.
als Linearkombination der periodischen Sinus- und Cosinus-Funktionen zu beschreiben.
 gut approximiert, also annähert.
gut approximiert, also annähert.Dabei sollten generell zwei Typen der gegebenen Funktion  unterschieden werden: Periodische Funktionen und nicht-periodische Funktionen.
unterschieden werden: Periodische Funktionen und nicht-periodische Funktionen.
Periodische Funktionen: Fourier-Reihe
Eine Funktion  wird als periodisch mit Periode T bezeichnet, falls für alle
wird als periodisch mit Periode T bezeichnet, falls für alle  gilt:
gilt:  . Eine solche T-periodische Funktion
. Eine solche T-periodische Funktion  lässt sich auf dem Intervall
lässt sich auf dem Intervall ![Rendered by QuickLaTeX.com [-T/2,\ \ T/2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-105e7af0d227d898ec1f74abb14acc6a_l3.png) unter bestimmten Voraussetzungen gut durch die folgende trigonometrische Reihe
unter bestimmten Voraussetzungen gut durch die folgende trigonometrische Reihe ![Rendered by QuickLaTeX.com \mathfrak{F}[f]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1778d77d77446d1bcaea9d12ac782419_l3.png) approximieren:
approximieren:
![Rendered by QuickLaTeX.com \mathfrak{F}\left[f\right]\left(t\right)=\frac{a_0}{2}+\sum_{k=1}^{\infty}\left[a_k\cdot\cos{\left(k\cdot\frac{2\pi}{T}\cdot t\right)}+b_k\cdot s i n{\left(k\cdot\frac{2\pi}{T}\cdot t \right)}\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0f06217a3ed02f9536b46031b752dec3_l3.png)
Dabei berechnen sich die Entwicklungskoeffizienten  und
und  folgendermaßen:
folgendermaßen:




Wird  als Grundfrequenz bezeichnet, so wird also
als Grundfrequenz bezeichnet, so wird also  durch eine Summe von Sinus- und Cosinus-Funktionen unterschiedlicher Amplituden dargestellt, deren Frequenzen ein positiv ganzzahliges Vielfaches
durch eine Summe von Sinus- und Cosinus-Funktionen unterschiedlicher Amplituden dargestellt, deren Frequenzen ein positiv ganzzahliges Vielfaches  der Grundfrequenz
der Grundfrequenz 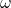 sind.
sind.
Werden die trigonometrischen Funktionen mithilfe der Eulerschen Formel durch


ersetzt, so ergibt sich die\ folgende etwas übersichtlichere Darstellung dieser trigonometrischen Reihe:
![Rendered by QuickLaTeX.com \mathfrak{F}\left[f\right]\left(t\right)=\sum_{k=-\infty}^{\infty}c_k\cdot e^{i\cdot \omega_k\cdot t}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-be964e62a06bac9c1b04142b4075f081_l3.png)
Die Koeffizienten  berechnen sich hierfür wie folgt:
berechnen sich hierfür wie folgt:

Die Reihe ![Rendered by QuickLaTeX.com \mathfrak{F}[f]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1778d77d77446d1bcaea9d12ac782419_l3.png) wird als Fourier-Reihe
der T-periodischen Funktion
wird als Fourier-Reihe
der T-periodischen Funktion  bezeichnet. Ist diese Funktion stückweise stetig differenzierbar, so konvergiert die Fourier-Reihe gleichmäßig gegen
bezeichnet. Ist diese Funktion stückweise stetig differenzierbar, so konvergiert die Fourier-Reihe gleichmäßig gegen  . Ist
. Ist  allerdings nur stetig in
allerdings nur stetig in ![Rendered by QuickLaTeX.com [-T/2,\ \ T/2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-105e7af0d227d898ec1f74abb14acc6a_l3.png) so konvergiert die Fourier-Reihe nur im quadratischen Mittel gegen die Funktion
so konvergiert die Fourier-Reihe nur im quadratischen Mittel gegen die Funktion  (Dirichlet-Bedingung bzw. Satz von Dirichlet).
(Dirichlet-Bedingung bzw. Satz von Dirichlet).
Durch Bestimmung der Fourier-Reihe erhält man ein sogenanntes Frequenzspektrum, das jeder Frequenz  die Amplitude der Schwingung
die Amplitude der Schwingung  zuordnet. In der Akustik kann somit ein Geräusch, das sich aus Tönen verschiedener Frequenzen zusammensetzt, in seine Einzeltöne mit Angabe derer Frequenz und Amplitude zerlegt werden.
zuordnet. In der Akustik kann somit ein Geräusch, das sich aus Tönen verschiedener Frequenzen zusammensetzt, in seine Einzeltöne mit Angabe derer Frequenz und Amplitude zerlegt werden.
Allerdings wurde eingangs an die Funktion  die wichtige Voraussetzung gestellt, dass sie periodisch sein muss, weshalb eine Analyse des Frequenzspektrums auf diese Weise nur für periodische Signale möglich ist. Da solche Signale in der Praxis allerdings nur selten auftreten ist es von Interesse auch für nicht-periodische Funktionen das Frequenzspektrum bestimmen zu können.
die wichtige Voraussetzung gestellt, dass sie periodisch sein muss, weshalb eine Analyse des Frequenzspektrums auf diese Weise nur für periodische Signale möglich ist. Da solche Signale in der Praxis allerdings nur selten auftreten ist es von Interesse auch für nicht-periodische Funktionen das Frequenzspektrum bestimmen zu können.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Nicht-Periodische Funktionen: Fourier-Integral
Das Ziel der Fourier Transformation ist es, auch nicht-periodische Funktionen durch Linearkombination der trigonometrischen Funktionen approximieren zu können. Dafür wird das Wissen über T-periodische Funktionen genutzt und weitergetragen. Die Grundidee dabei ist, dass eine nicht-periodische Funktion  als periodische Funktion aufgefasst wird, deren Periode allerdings unendlich groß ist. Das führt zu folgendem Phänomen: Während der Abstand
als periodische Funktion aufgefasst wird, deren Periode allerdings unendlich groß ist. Das führt zu folgendem Phänomen: Während der Abstand  zweier benachbarter Frequenzen
zweier benachbarter Frequenzen  und
und  für eine endliche Periode T genau
für eine endliche Periode T genau  beträgt, verschwindet dieser Abstand im Grenzfall
beträgt, verschwindet dieser Abstand im Grenzfall  :
:

Das bedeutet, dass durch den Übergang von einer endlichen Periode T zu einer unendlich großen Periode  aus einem diskreten Frequenzspektrum ein kontinuierliches Frequenzspektrum wird.
aus einem diskreten Frequenzspektrum ein kontinuierliches Frequenzspektrum wird.
Die genaueren Folgen des Übergangs  sollen nun anhand der Fourier-Reihe
sollen nun anhand der Fourier-Reihe ](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-367afce7ebe572a3d074b9e21ac3eb24_l3.png) betrachtet werden. Dazu wird in die Formel
betrachtet werden. Dazu wird in die Formel ![Rendered by QuickLaTeX.com \mathfrak{F}[f]t=\sum_{k=-\infty}^{\infty}c_k\cdot \ e^{i\cdot\omega_k\cdot t}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-455021a33da25342620904847e2d6bd6_l3.png) zunächst die Amplitude
zunächst die Amplitude  eingesetzt und es ergibt sich:
eingesetzt und es ergibt sich:
 = \sum_{k=-\infty}^{\infty}{\frac{1}{T}\int_{-T/2}^{\ \ T/2}{\ f\left(\tau\right)}{\cdot e}^{-i\cdot \omega_k\cdot \tau}d\tau}\cdot \ e^{i\cdot \omega_k\cdot t}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dbc53d72f7c18db50f1a1f8efe72d5c6_l3.png)
Durch Einsetzen der Beziehung  folgt weiter:
folgt weiter:
=\sum_{k=-\infty}^{\infty}{\frac{1}{2\pi}\int_{-T/2}^{\ \ T/2}{\ f\left(\tau\right)\cdot e}^{-i\cdot\omega_k\cdot \tau}d\tau}\cdot e^{i\cdot \omega_k\cdot t}\cdot \Delta \omega](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fa372826e95d328527a6b72fe8cced31_l3.png)
Wird nun  durch
durch  ersetzt, so erhält man den folgenden Ausdruck:
ersetzt, so erhält man den folgenden Ausdruck:
![Rendered by QuickLaTeX.com \mathfrak{F}[f]\left(t\right)=\frac{1}{2\pi}\sum_{k=-\infty}^{\infty}{\widetilde{f}\left(\omega_k\right)}\cdot e^{i\cdot\omega_k\cdot t}\cdot \Delta \omega](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c0e364da2e38e22ff5ec64c1b99b1f10_l3.png)
Dies stellt eine Riemannsche Summe mit der Zerlegung  dar. Betrachtet man nun den Grenzübergang
dar. Betrachtet man nun den Grenzübergang  , so gilt wie bereits gezeigt
, so gilt wie bereits gezeigt  und aus den diskreten Werten
und aus den diskreten Werten  wird eine Funktion:
wird eine Funktion:
![Rendered by QuickLaTeX.com \mathcal{F}\left[f\right]\left(\omega\right)=\hat{f}\left(\omega\right):=\int_{-\infty}^{\infty}{f(\tau)\cdot e^{-i\cdot\omega\cdot\tau} d\tau}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d38c65571eff2fd6e76bc8f721e35ff3_l3.png)
Außerdem wird im Grenzübergang  aus der Summe ein Integral und es ergibt sich das Fourier-Integral
aus der Summe ein Integral und es ergibt sich das Fourier-Integral ![Rendered by QuickLaTeX.com \mathcal{F}^{-1}\left[\hat{f}\right]\left(t\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-df463172d40b17c1aa439df73f8c92e3_l3.png) :
:
![Rendered by QuickLaTeX.com \mathcal{F}^{-1}\left[\hat{f}\right]\left(t\right)=\frac{1}{2\pi}\int_{-\infty}^{\ \ \infty}{\hat{f}\left(\omega\right)}{\cdot e}^{i\cdot\omega\cdot t}d\omega](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-18f55c14d7c556cb4fcaf23417e38a77_l3.png)
Fourier Transformation Formel
Vergleicht man das oben hergeleitete Fourier-Integral mit der ursprünglichen Formulierung der Fourier-Reihe so werden gewisse Analogien sichtbar.
Während für periodische Funktionen zu den diskreten Frequenzen  die Amplitude
die Amplitude  gehört, ergibt sich für nicht-periodische Funktionen eine Amplituden-Funktion
gehört, ergibt sich für nicht-periodische Funktionen eine Amplituden-Funktion  in Abhängigkeit der kontinuierlichen Frequenzen
in Abhängigkeit der kontinuierlichen Frequenzen 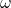 . Die Funktion
. Die Funktion  wird als Fourier-Transformierte von
wird als Fourier-Transformierte von  bezeichnet. Sie stellt das Frequenzspektrum der Funktion
bezeichnet. Sie stellt das Frequenzspektrum der Funktion  dar und die Fourier Transformation ist nichts anderes als die Operation ihrer Bestimmung. Eine alternative Schreibweise für die Fourier-Transformierte
dar und die Fourier Transformation ist nichts anderes als die Operation ihrer Bestimmung. Eine alternative Schreibweise für die Fourier-Transformierte  ist
ist ![Rendered by QuickLaTeX.com \mathcal{F}\left[f\right]\left(\omega\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0839a5402d87088cc3f5ced1842fe728_l3.png) . Die Umkehroperation der Fourier Transformation ist die sogenannte inverse Fourier Transformation
. Die Umkehroperation der Fourier Transformation ist die sogenannte inverse Fourier Transformation  und das Fourier-Integral
und das Fourier-Integral ![Rendered by QuickLaTeX.com \mathcal{F}^{-1}\left[\hat{f}\right]\left(t\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-df463172d40b17c1aa439df73f8c92e3_l3.png) wird auch als inverse Fourier-Transformierte bezeichnet.
wird auch als inverse Fourier-Transformierte bezeichnet.
Umkehrformel: Inverse Fourier Transformation
Sei  sowie
sowie  , dann ist die inverse Fourier-Transformierte gegeben durch:
, dann ist die inverse Fourier-Transformierte gegeben durch:
![Rendered by QuickLaTeX.com \mathcal{F}^{-1}\left[\hat{f}\right]\left(t\right)=\frac{1}{2\pi}\int_{-\infty}^{\ \ \infty}{\hat{f}\left(\omega\right)}{\cdot e}^{i\cdot\omega\cdot t}d\omega](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-18f55c14d7c556cb4fcaf23417e38a77_l3.png)
Unter den gegebenen Voraussetzungen gilt an allen Stetigkeitsstellen von  :
:
![Rendered by QuickLaTeX.com \mathcal{F}^{-1}\left[\hat{f}\right]\left(t\right)=f(t)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2b6dc9ffa5bf6019f784a41871b458e6_l3.png)
Die inverse Fourier-Transformierte wird auch als Fourier-Integral oder spektrale Zerlegung von  bezeichnet.
bezeichnet.
Wird aus der Fourier-Transformierten wieder die Originalfunktion f über das Fourier-Integral bestimmt, so spricht man auch von der inversen Fourier-Transformation, der Fouriersynthese oder auch der Rücktransformation.
Anwendungen der Fourier Transformation
Die Fourier Transformation bzw. die Fourier Analyse und Fourier-Synthese im Allgemeinen haben vor allem in den Ingenieurswissenschaften und der Physik wichtige Anwendungen. Ist dabei die Originalfunktion in Abhängigkeit der Zeit gegeben, so erfolgen Rechnungen mit der Originalfunktion im sogenannten Zeitbereich. Hängt sie jedoch vom Ort ab, so ist dabei die Rede vom Ortsbereich. Rechnungen mit der Fourier Transformierten bzw. der Bildfunktion – also nach der Fourier Transformation – erfolgen im sogenannten Frequenz- bzw. Bildbereich. In der Technik wird häufig zu einer Originalfunktion  im Zeitbereich die zugehörige Bildfunktion im Frequenzbereich mit
im Zeitbereich die zugehörige Bildfunktion im Frequenzbereich mit  symbolisiert und deren Zuordnung folgendermaßen dargestellt:
symbolisiert und deren Zuordnung folgendermaßen dargestellt:
Für die Praxis der Signalverarbeitung ist die Fouriertransformation allerdings etwas ungeeignet, da die Berechnungsvorschrift der Fourier-Transformierten für ein kontinuierliches Signal gilt. In der Praxis können allerdings nur diskrete Signale verarbeitet werden. Hier ist dann die sogenannte Diskrete Fourier Transformation (DFT) ein geeignetes Mittel, um das Frequenzspektrum des Signals zu ermitteln. Einen Algorithmus hierfür liefert die Fast Fourier Transformation (FFT) also die Schnelle Fourier Transformation.
Eigenschaften der Fourier Transformation
Um die Fourier Transformierte einer Funktion zu bestimmen ist es nicht immer von Nöten diese mithilfe der Definition explizit zu berechnen. Stattdessen kann auf bereits bekannte Fouriertransformationen zurückgegriffen werden, die dann mithilfe gewisser Rechenregeln an die neue Funktion angepasst werden. Die wichtigsten Rechenregeln hierfür sollen im Folgenden dargelegt werden.
Rechenregeln
Es sei  . Dann gilt:
. Dann gilt:
Linearität
![Rendered by QuickLaTeX.com \mathcal{F}\left[f+g\right]\left(\omega\right)=\mathcal{F}\left[f\right]\left(\omega\right)+\mathcal{F}\left[g\right]\left(\omega\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5878891f42bcdb045dfc51f027c4b8e7_l3.png)
![Rendered by QuickLaTeX.com \mathcal{F}\left[a\cdot f\right]\left(\omega\right)=a\cdot\mathcal{F}\left[f\right]\left(\omega\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-45579775a45e8ba0c19221819bf780f7_l3.png) für
für 
Streckung
![Rendered by QuickLaTeX.com \mathcal{F}\left[f(c\cdot t)\right]\left(\omega\right)=\frac{1}{|c|}\mathcal{F}\left[f\right]\left(\frac{\omega}{c}\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5d3044e1c7f6b6dec35e0ed1a5113837_l3.png)
Konjugation
![Rendered by QuickLaTeX.com \mathcal{F}\left[\bar{f(t)}\right]\left(\omega\right)=\ \bar{\mathcal{F}\left[f(-t)\right]\left(\omega\right)}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b56031c169c3f1e6a62be08bef5f49a6_l3.png)
Verschiebung
![Rendered by QuickLaTeX.com \mathcal{F}\left[f\left(t-a\right)\right]\left(\omega\right)=e^{-i\omega a}\cdot\mathcal{F}\left[f\right]\left(\omega\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f6779036325f4037cb473e2cadb8dc45_l3.png)
![Rendered by QuickLaTeX.com \mathcal{F}\left[e^{iat}\cdot f(t)\right]\left(\omega\right)=\mathcal{F}\left[f\right]\left(\omega-a\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-90cdb30932c5f960fbee16eb45ddecbf_l3.png)
Faltung 
![Rendered by QuickLaTeX.com \mathcal{F}\left[f\cdot g\right]\left(\omega\right)=\mathcal{F}\left[f\right]\left(\omega\right)\cdot\mathcal{F}\left[g\right]\left(\omega\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-52effa0b9474e42349631a1c3b3dff77_l3.png)
![Rendered by QuickLaTeX.com \mathcal{F}\left[f\cdot g\right]\left(\omega\right)=\frac{1}{2\pi}\left(\mathcal{F}\left[f\right]\cdot\mathcal{F}\left[f\right]\right)\left(\omega\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1f08fa1869cd0f7e5aa1306b19134549_l3.png)
Fourier Transformation Beispiel
Bevor in einer Tabelle die wichtigsten Fouriertransformationen aufgelistet werden, soll zunächst noch anhand zweier Beispiele die Fourier Transformation konkret durchgeführt werden.
Fourier Transformation Beispiel – Rechteckfunktion
Im Folgenden soll die Fourier Transformation für den Rechteckimpuls

dargelegt werden, d.h. es soll die Fourier-Transformierte

ermittelt werden. Da der Rechteckimpuls nur zwischen  und
und  Werte ungleich Null annimmt, vereinfacht sich das Integral zu:
Werte ungleich Null annimmt, vereinfacht sich das Integral zu:

Dieses Integral lässt sich nun mithilfe der Stammfunktion von  berechnen:
berechnen:
![Rendered by QuickLaTeX.com \hat{f}\left(\omega\right)=\int_{-a}^{\ \ a}{\ 1}{\cdot e}^{-i\cdot \omega\cdot \tau}d\tau=\left[-\frac{1}{i\omega}{\cdot e}^{-i\cdot \omega\cdot \tau}\right]_{-a}^{\ \ \ a}=-\frac{1}{i\omega}\left(e^{-i\cdot \omega\cdot a}{-e}^{i\cdot \omega\cdot a}\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1ed27417ea5ae3e8adf316ef1d7e7470_l3.png)
Mithilfe der Eulerschen Formel  ergibt sich
ergibt sich 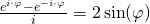 und es folgt somit:
und es folgt somit:

Fourier Transformation Beispiel – Endlicher Wellenzug
Als zweites Beispiel wird die Fourier Transformierte der Funktion  bestimmt, welche eine Schwingung beschreibt, die auf das Intervall von
bestimmt, welche eine Schwingung beschreibt, die auf das Intervall von  bis
bis  begrenzt ist:
begrenzt ist:

Wie im ersten Beispiel vereinfacht sich das Integral, da  nur für
nur für  ungleich Null ist:
ungleich Null ist:

Als nächstes lassen sich die Exponentialfunktionen zusammenfassen:

Dieses Integral lässt sich nun wieder elementar berechnen:
![Rendered by QuickLaTeX.com \hat{f}\left(\omega\right)=\int_{-a}^{\ \ a}{\ e^{i\left(\omega_0-\omega\right)t}}d\tau=\left[\frac{1}{i\left(\omega_0-\omega\right)}e^{i\left(\omega_0-\omega\right)t}\right]_{-a}^{\ \ \ a}=\frac{1}{i\left(\omega_0-\omega\right)}\left(e^{i\left(\omega_0-\omega\right)a}-e^{-i\left(\omega_0-\omega\right)a}\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3af48d92f8553e39d6d38a86c449b344_l3.png)
Wie im ersten Beispiel ergibt sich mithilfe der Euler-Formel:

Die Fourier-Transformierte  dieser Funktion ähnelt also derjenigen der Rechtecksfunktion und ist lediglich verschoben.
dieser Funktion ähnelt also derjenigen der Rechtecksfunktion und ist lediglich verschoben.
Fourier Transformation Übungsaufgabe I
Um dein Wissen zur Fourier Transformation zu vertiefen, schauen wir uns eine ausführliche Übungsaufgabe an.
Wie du die Lösung der Aufgabe Schritt für Schritt berechnest, erklären wir dir zunächst in der Übungsaufgabe I .
Fourier Transformation Übungsaufgabe II
In der Übungsaufgabe II führen wir die Berechnung fort.
In der Aufgabenstellung ist folgender Dreieckimpuls gegeben. Zu diesem soll die Fourier-Transformierte  der zugehörigen Funktion
der zugehörigen Funktion  berechnet werden.
berechnet werden.


 -Raum ist folgendermaßen definiert:
-Raum ist folgendermaßen definiert:
![Rendered by QuickLaTeX.com \mathcal{F}\left[f\right]\left(\omega\right)=\hat{f}\left(\omega\right:=](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-39025ac673729c869a9bb2df1a1d463b_l3.png)





