Weg-Zeit-Diagramm
Du fragst dich, was ein Weg-Zeit-Diagramm ist? Welche Aussage dahinter steckt und wie du es interpretieren kannst, erfährst du in unserem Beitrag und in unserem Video !
Weg-Zeit-Diagramm einfach erklärt
Ein Körper, der sich bewegt, legt in einer bestimmten Zeit einen bestimmten Weg zurück. Ein Auto kann zum Beispiel in einer Stunde einen Weg von 50 Kilometern zurücklegen. In einem Weg-Zeit-Diagramm kannst du so eine Bewegung in einem Koordinatensystem darstellen. Es zeigt dir den Zusammenhang zwischen dem zurückgelegten Weg und der dabei vergangenen Zeit in Form eines Graphen.
Auf der waagerechten x-Achse befindet sich die Zeit t und auf der senkrechten y-Achse der Weg s. Deswegen heißt das Weg-Zeit-Diagramm auch s-t-Diagramm. 
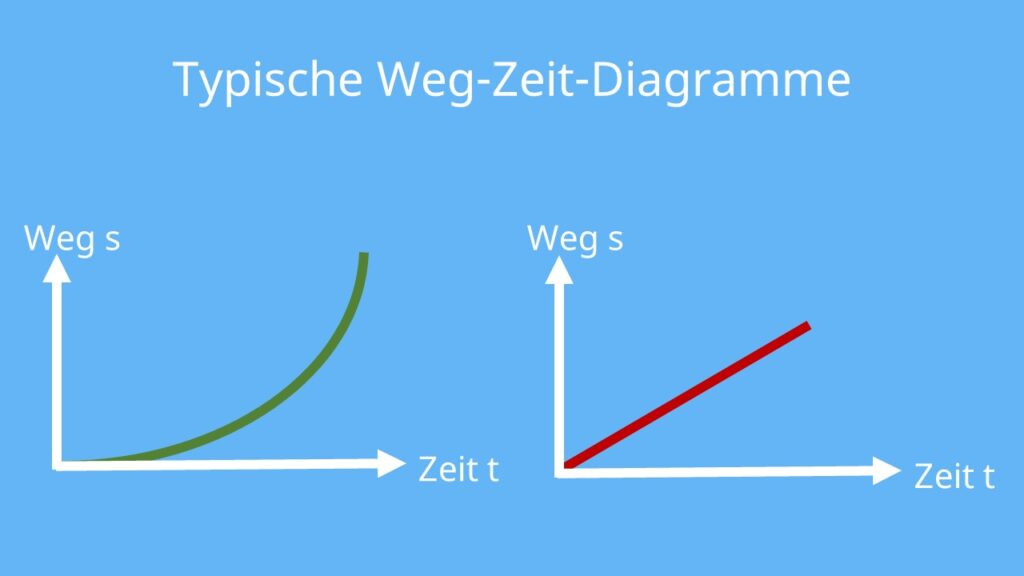
Bewegt sich der Körper mit konstanter Geschwindigkeit, ist der Graph eine Gerade. Bewegt sich der Körper hingegen mit konstanter Beschleunigung, ist der Graph eine Parabel. Die Steigung des Graphen ergibt die Geschwindigkeit v, mit der sich der Körper fortbewegt.
Weg-Zeit-Diagramm verstehen
Wenn sich ein Körper bewegt, legt er einen bestimmten Weg s in einer bestimmter Zeit t zurück. Stelle dir ein Auto vor, das eine Straße entlang fährt. Du misst jede Stunde, wie viele Kilometer das Auto zurückgelegt hat:
| Zeit t | 1 h | 2 h | 3 h | 4 h | 5 h |
| Weg s | 50 km | 100 km | 150 km | 200 km | 250 km |
Diese Punkte trägst du in ein Koordinatensystem ein und verbindest sie zu einer Linie. Daraus ergibt sich ein s-t-Diagramm. 
Schauen wir uns die Bewegung des Autos genauer an:
- In einer Stunde fährt das Auto 50 km. Das sind also 50 km / 1 h = 50 km pro Stunde.
- Nach zwei Stunden hat es 100 km zurückgelegt. Auch das sind 100 km / 2 h = 50 km pro Stunde.
- In drei Stunden fährt das Auto 150 km. Wir kommen wieder auf 150 km / 3 h = 50 km pro Stunde.
Das Auto legt also konstant 50 km pro Stunde zurück. Damit weißt du, mit welcher Geschwindigkeit das Auto fährt: 50 km/h. Die Geschwindigkeit v, die wir berechnet haben, ist die Steigung des Graphen im s-t-Diagramm. Du bestimmst die Geschwindigkeit mit der Formel: Geschwindigkeit v ist gleich zurückgelegter Weg s geteilt durch vergangene Zeit t.
![\[v = \frac{\Delta{s}}{\Delta{t}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-88b8abaf0e810a1ef3ca66ed0282b697_l3.png "Rendered by QuickLaTeX.com")
In unserem Beispiel fährt das Auto immer gleich schnell (konstante Geschwindigkeit), deshalb ist der Graph im Weg-Zeit Diagramm eine Gerade. Das Auto kann aber auch beschleunigen oder abbremsen, also schneller oder langsamer werden (konstante Beschleunigung). Die beiden Fälle schauen wir uns nun genauer an.
s-t-Diagramm mit konstanter Geschwindigkeit
Bewegt sich ein Körper mit konstanter, also mit gleichbleibender Geschwindigkeit, ist die Steigung des Graphen überall gleich. Der Körper bremst nie ab und beschleunigt auch nicht. Das bedeutet, der Graph ist eine Gerade.
Dabei gilt:
s ~ t
Das bedeutet, Weg und Zeit sind proportional, also nehmen gleichmäßig zueinander zu. Verdoppelt sich die Zeit, verdoppelt sich also auch der Weg. Du sprichst von einer gleichförmig geradlinigen Bewegung oder von einer gleichförmigen Kreisbewegung.
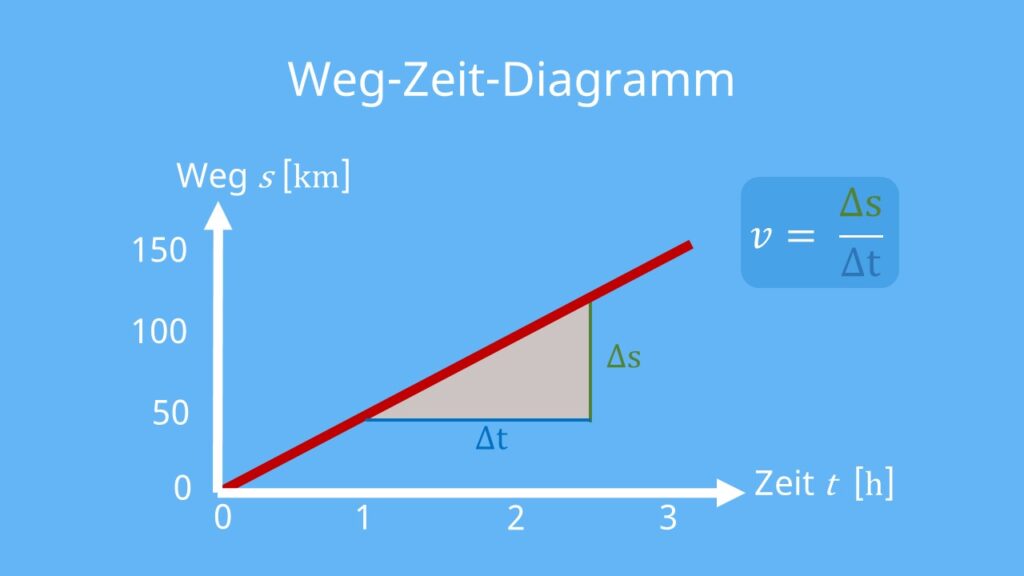
Je steiler der Graph, desto größer die Geschwindigkeit, mit der sich der Körper fortbewegt. Du bestimmst die Geschwindigkeit mit folgender Formel:
∆s ist die zurückgelegte Strecke s zwischen zwei Zeitpunkten. ∆t ist die Differenz, also der Unterschied, zwischen diesen beiden Zeitpunkten. 
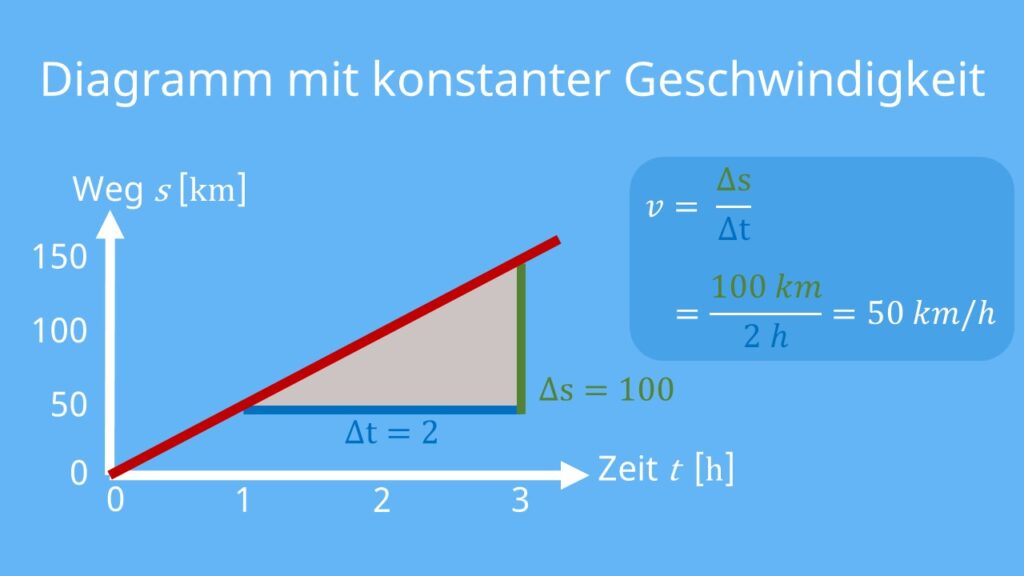
In unserem Beispiel gilt ∆s = 100 km und ∆t = 2 h. Als Geschwindigkeit ergibt sich dann:
![\[v = \frac{\Delta{s}}{\Delta{t}} = \frac{100 \text{km}}{2 \text{h}} = 50 \frac{\text{km}}{\text{h}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a17c10ad6313fe86d029b1eed7472f99_l3.png "Rendered by QuickLaTeX.com")
Da der Weg in Kilometer und die Zeit in Stunden angegeben sind, hat die Geschwindigkeit die Einheit km/h. Das Auto fährt also mit einer konstanten Geschwindigkeit von 50 km/h.
s-t-Diagramm mit konstanter Beschleunigung
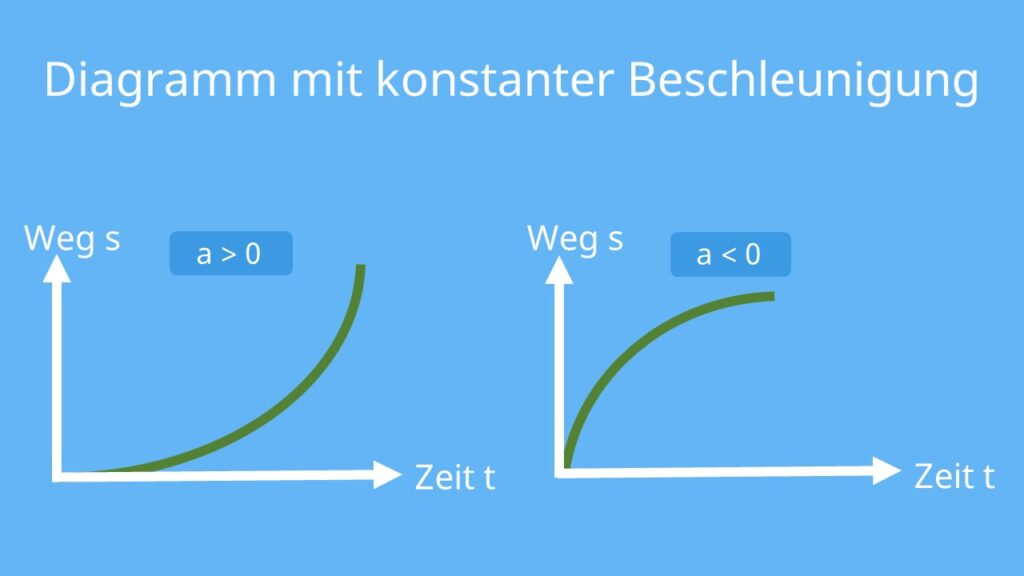
Bewegt sich ein Körper mit konstanter bzw. gleichmäßiger Beschleunigung a, nimmt seine Geschwindigkeit zu oder ab. Das bedeutet, dass sich die Steigung des Graphen verändert. Der Graph der konstanten Beschleunigung ist eine Parabel.
Dabei gilt:
s ~ t 2
Das bedeutet, der Weg s nimmt mit dem Quadrat der Zeit t zu. Verdoppelt sich die Zeit, vervierfacht sich der Weg. Du sprichst von einer gleichmäßig beschleunigten gleichförmigen Bewegung.
Ist die Parabel nach oben geöffnet, nimmt die Geschwindigkeit zu und der Körper beschleunigt (a>0). Ist die Parabel hingegen nach unten geöffnet, nimmt die Geschwindigkeit ab und der Körper bremst (a<0). Je steiler die Parabel verläuft, desto höher ist die Beschleunigung des Körpers. 
Spezielle Formen der konstanten Beschleunigung sind die gleichmäßig beschleunigte Kreisbewegung und der freie Fall.
Geschwindigkeit
Du weißt nun, dass die Steigung im Weg-Zeit-Diagramm die Geschwindigkeit v ergibt. Wie du die Geschwindigkeit berechnen kannst, zeigen wir dir hier und in unserem Video! 
