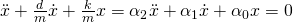Schwingungen
Dich interessiert, wie die Federung eines Autos funktioniert und du willst wissen was dabei für Schwingungen entstehen? Das erklären wir dir in diesem Beitrag.
Inhaltsübersicht
Mathematische Beschreibung von Schwingungen
Allgemein wird eine periodische Bewegung unter Einfluss von Potentialkräften als Schwingung bezeichnet. Bei der Pendelbewegung z.B. ist die Potentialkraft, die Gewichtskraft. Diese Schwingungen sind in der Regel nicht endlos, weil das System meistens gedämpft wird. Diese Dämpfung ist in der Regel geschwindigkeitsabhängig.
Parameter von Schwingungen
Bei Schwingungen gibt es allgemein zwei Parameter, die sie beschreiben:
- Die Amplitude a, die den maximalen Ausschlag zur Ruhelage angibt
- Und die Periodendauer T, die die Zeit angibt, die für eine ganze Schwingung benötigt wird bzw. die Kreisfrequenz Omega, die gebildet wird durch:
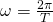
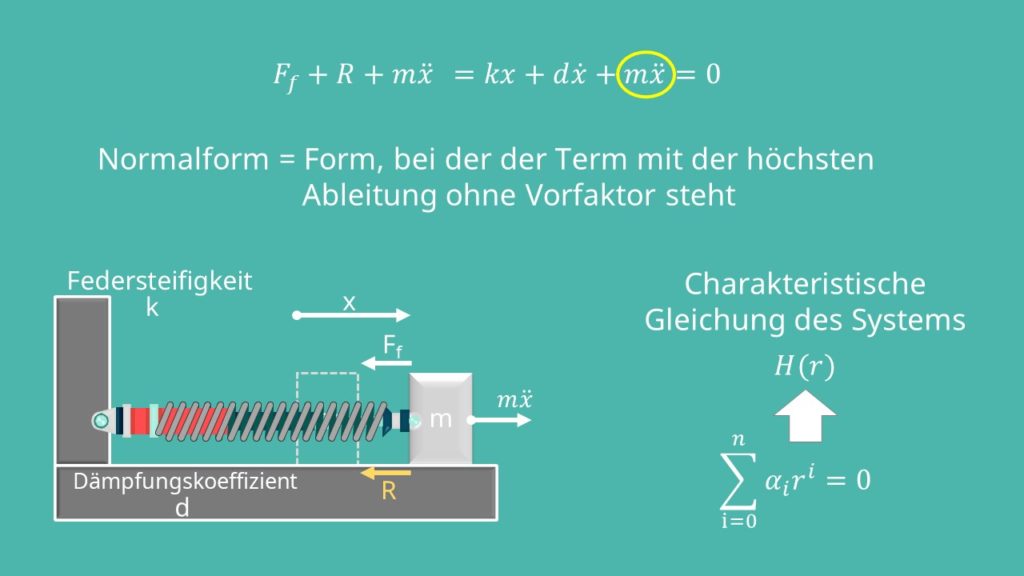
Im Rahmen der Schwingungslehre kann man zwischen der Eigenschwingung, der angefachten Schwingung und der fremderregten Schwingung unterscheiden. Wir beginnen zunächst mit der Eigenschwingung. Hier wirken nur Kräfte, die von der Systembewegung abhängen. Dafür betrachten wir zur Anschauung ein Feder-Masse-System. Das System besteht aus einer Feder mit der Federsteifigkeit k, die die Federkraft Ff erzeugt, die die Wand und eine Masse mit dem Gewicht m verbindet. Die Schwingung wird gedämpft durch die Reibkraft R mit dem Dämpfungskoeffizienten d. Da wir die Bewegung der Masse mathematisch beschreiben wollen, verwenden wir x als zeitabhängige Koordinate, die den Ort der Masse gegenüber der Anfangslage beschreibt. Wir nehmen diese positiv nach rechts an. Wir nutzen jetzt das d’Alembert’sche Prinzip zur Aufstellung der Differentialgleichung. Das heißt wir führen eine Hilfskraft ein, die in positive Koordinatenrichtung zeigt. Damit ergibt sich:
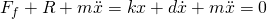
Wir erhalten also mit den konstanten Faktoren k und D eine gewöhnliche lineare Differentialgleichung des Typs:
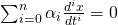
Lösen der Differentialgleichung
Diese Differentialgleichung ist n-ter Ordnung. Das heißt, wir haben n-Terme und n Ableitungen. Die Gleichung in unserem Beispiel ist also zweiter Ordnung. Solche gewöhnlichen Differentialgleichungen werden in der Regel gelöst mit dem Ansatz:
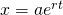
Das liegt daran, dass wir mit der eulerschen Zahl immer wieder die Grundfunktion in der Ableitung stehen haben.
Wir erhalten damit:
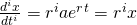
Wir können die gewöhnliche Differentialgleichung damit um schreiben in:
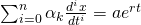
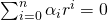
Da der Faktor vor der Summe für alle i konstant ist, bezeichnen wir:
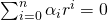
als charakteristische Gleichung des Systems. Diese liefert uns Lösungen für r, die das System beschreiben und wird kurz als H(r) bezeichnet. Dementsprechend wollen wir unser System nun auch lösen. Dafür bringen wir die Differentialgleichung in Normalform und leiten daraus die charakteristische Gleichung ab. Die Normalform ist die Form, bei der der Term mit der höchsten Ableitung ohne Vorfaktor steht. Das kommt dir vielleicht bekannt vor. Das liegt daran, dass du bei der pq-Formel auch den höchsten Term, also den quadratischen Term, einzeln stehen haben möchtest. In unserem Fall ergibt sich die Normalform zu: