Raketengleichung
Du möchtest wissen, was es mit der Raketengleichung auf sich hat? Dann schau dir unseren Beitrag und das Video dazu an.
Inhaltsübersicht
Impuls und Impulserhaltungssatz
Die Raketengleichung oder Raketengrundgleichung beschreibt die Bewegungsgleichung einer sonst kräftefreien Rakete. Diese beschleunigt durch einen kontinuierlichen Ausstoß des Treibstoffs und unterliegt keinem Luftwiderstand. Die Raketengleichung basiert auf dem Impuls und dem Impulserhaltungssatz.
Der Impuls 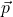 ist eine vektorielle Größe, die du durch die Masse m und die Geschwindigkeit
ist eine vektorielle Größe, die du durch die Masse m und die Geschwindigkeit 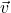 eines Körpers beschreibst.
eines Körpers beschreibst.
![Rendered by QuickLaTeX.com \[\vec{p} = m \cdot \vec{v}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0c9fbe40f97b6f1890b1fa71270f8103_l3.png)
Die Einheit für den Impuls ist Newton mal Sekunde [Ns]. Impulserhaltung hingegen bedeutet, dass in einem kräftefreien abgeschlossenen System der Gesamtimpuls konstant bleibt. Das bedeutet, dass der Impuls vor einer Wechselwirkung gleich dem Impuls nach dieser ist. Außerdem ist der Zusammenhang mit der Kraft durch die zeitliche Ableitung des Impulses gegeben.
![Rendered by QuickLaTeX.com \[\vec{F} = \frac{d\vec{p}}{dt} = \frac{d(m \cdot \vec{v})}{dt}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-5f974f95690985007ed51c5d3bc12dbe_l3.png)
Raketengrundgleichung
Die Raketengrundgleichung ist die Bewegungsgleichung einer idealisierten Rakete. Sie beschreibt die Geschwindigkeitszunahme, aufgrund des kontinuierlichen Ausstoßes von Stützmasse. In der Raketengrundgleichung wird kein Luftwiderstand und keine Gravitation, aber ein kontinuierlicher Ausstoß des Treibstoffes angenommen.
Die Rakete ist also frei von äußeren Kräften und der Impulserhaltungssatz kann angewendet werden. Damit leitest du die Raketengleichung her.
Raketengleichung Herleitung
Die Herleitung der Raketengrundgleichung funktioniert über die Impulserhaltung der Rakete. Der gesamte Impuls für die Rakete besteht aus der Rakete selbst und dem Impuls, der durch den Ausstoß des Treibstoffes zustande kommt. Durch den Ausstoß verändert sich die Masse der Rakete und es kommt daher zu einer Impulsänderung über die Zeit.
![Rendered by QuickLaTeX.com \[\frac{d\vec{p}}{dt} = \frac{d(m\cdot \vec{v})}{dt} = m \cdot \dot{\vec{v}} + \dot{m} \cdot \vec{v}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-694fc6fa9ef2e615d49fa09a02402a4e_l3.png)
Die Masse verändert sich also durch den Austritt des Treibstoffes mit der Zeit. Der Ausstoß geschieht mit einer bestimmten Geschwindigkeit, der Austrittsgeschwindigkeit oder auch Ausströmgeschwindigkeit. Diese Geschwindigkeit muss negativ sein, da sie entgegen der Bewegungsrichtung der Rakete verläuft. So kann festgehalten werden:
![Rendered by QuickLaTeX.com \[\dot{m} \cdot \vec{v} = -\vec{v_A} \cdot \dot{m}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c6ded1000dd01acf8b706669ad7612a1_l3.png)
Da ein kräftemäßig abgeschlossenes System betrachtet wird, muss aufgrund des Impulserhaltungssatzes die Veränderung des Gesamtimpulses über die Zeit null sein. So lässt sich schreiben:
![Rendered by QuickLaTeX.com \[\frac{d\vec{p}}{dt} = m \cdot \dot{\vec{v}} + (-\vec{v_A} \cdot \dot{m}) = 0\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-8f73ac2f302e4604f3b8d1847600c085_l3.png)
![Rendered by QuickLaTeX.com \[m \cdot \dot{\vec{v}} = -\vec{v_A} \cdot \dot{m}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6f82a5f62caa7a534c32ddc95c6a440d_l3.png)
Das ist eine Differentialgleichung 1. Ordnung, da Variablen und deren erste Ableitung in einer Gleichung vorkommen. Solche Gleichungen werden durch eine Trennung der Variablen und einer Integration gelöst. Zuerst wird aber noch die Bewegungsgleichung mit dt multipliziert.
![Rendered by QuickLaTeX.com \[m \cdot \frac{d\vec{v}}{dt} = -\vec{v_A} \cdot \frac{dm}{dt}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-fa29e87e01157a2d748b9e574ddde5b4_l3.png)
![Rendered by QuickLaTeX.com \[m \cdot d\vec{v} = -\vec{v_A} \cdot dm\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2dbd77ed67899e71bba20dbbeb4e879a_l3.png)
Danach kommt die Trennung der Variablen:
![Rendered by QuickLaTeX.com \[\frac{dm}{m} = -\frac{d\vec{v}}{\vec{v_A}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-daf2b50a62c777037c12c19449458f94_l3.png)
Jetzt wird die Gleichung integriert:
![Rendered by QuickLaTeX.com \[\int\frac{dm}{m}\ =\ \int{-\frac{d\vec{v}}{\vec{v_A}}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-118c55643dfbd6ccb2c154beb75598c9_l3.png)
Um eine Integration durchzuführen, müssen die Integrationsgrenzen bestimmt werden. Für die Masse gilt, dass die Rakete eine Anfangsmasse m0 und eine Endmasse mE hat. Am Anfang ist sie mit Treibstoff beladen und am Ende ist dieser ausgestoßen und kann nicht mehr zum Gewicht der Rakete hinzugerechnet werden. Ebenfalls gibt es eine Anfangsgeschwindigkeit v0 und Endgeschwindigkeit vE. Im nächsten Schritt wird die Konstante aus der Integration gezogen und es ergeben sich die folgenden Integrale.
![Rendered by QuickLaTeX.com \[\int_{m_0}^{m_E}{\frac{1}{m}\ dm}\ =\ -\ \frac{1}{\vec{v_A}}\int_{v_0}^{v_E}dv\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f9cf5511506a4cb8bc1ce3806e80c8fd_l3.png)
Mit den jeweiligen Stammfunktionen:
![Rendered by QuickLaTeX.com \[\left[ln\left(m\right)\right]\begin{matrix}m_E\\m_0\\\end{matrix} = -\frac{1}{\vec{v_A}}\cdot\left[v\right]\begin{matrix}v_E\\v_0\\\end{matrix}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-1af80bd77c9c5aea6c1a5fc4d40c11c3_l3.png)
Dies aufgelöst und umgeschrieben ergibt:
![Rendered by QuickLaTeX.com \[ln(\frac{m_E}{m_0})\ =\ -\frac{1}{\vec{v_A}}\ \cdot\ (\vec{v_E}\ -\ \vec{v_0})\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f3fd18e79336bd945ae1318ddf3f142f_l3.png)
Die Raketengleichung der idealisierten Rakete lautet nun:
![Rendered by QuickLaTeX.com \[-\vec{v_A} \cdot \ln(\frac{m_E}{m_0}) = (\vec{v_E} - \vec{v_0})\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-608c8f5d7df996f5619e8582b0f2a41b_l3.png)
So kann aus einem Massenverhältnis die Endgeschwindigkeit der Rakete bestimmt werden, wenn die Anfangsgeschwindigkeit und die Ausströmungsgeschwindigkeit bekannt sind. Zum Schluss kann noch das Erdschwerefeld mitberücksichtigt werden. Dabei wird der abgeleitete Impuls mit der Schwerkraft gleichgesetzt, da die Ableitung des Impulses eine Kraft ist.
Hier lautet die Bewegungsgleichung:
![Rendered by QuickLaTeX.com \[\frac{d\vec{p}}{dt} = m \cdot \dot{\vec{v}} + \dot{m} \cdot \vec{v} = m \cdot g = \vec{F}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-45d03732760d41d454d70747ff8fc425_l3.png)
Die Differentialgleichung wird wieder durch Variablentrennung, Integration und Umstellung aufgelöst. Dadurch ergibt sich die Raketengleichung mit der Berücksichtigung des Schwerefeldes:
![Rendered by QuickLaTeX.com \[- \vec{v_A} \cdot ln(\frac{m_E}{m_0}) = \vec{v_E} + g \cdot T - \vec{v_0} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ccedc9f1d965384ba199db11cfa724cc_l3.png)
Die Variable g gibt dabei den Ortsfaktor
und T die Zeit der Brenndauer an. Die Formel ist allerdings ungeeignet für genaue Berechnungen, da sich beispielsweise 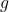 mit der zunehmenden Höhe der Rakete verändert.
mit der zunehmenden Höhe der Rakete verändert.
Geschwindigkeit Rakete
Als Beispiel wird die Endgeschwindigkeit einer Rakete mithilfe der Raketengleichung berechnet.
![Rendered by QuickLaTeX.com \[- \vec{v_A} \cdot ln(\frac{m_E}{m_0}) = (\vec{v_E} - \vec{v_0})\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-66cd512b14bbfa11cb6a87463c007431_l3.png)
Die Rakete fliegt bereits im All und wiegt 50 t. Zusätzlich hat sie noch Treibstoff mit der Masse von 80 t an Bord. Da sich der Flugkörper schon im All befindet, hat er eine Anfangsgeschwindigkeit von 180 m/s. Während des Fluges stößt die Rakete den Treibstoff mit einer konstanten Geschwindigkeit von 20 m/s aus.
Stellst du die Gleichung nach der Endgeschwindigkeit 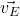 um, so erhältst du:
um, so erhältst du:
![Rendered by QuickLaTeX.com \[\vec{v_E} = - \vec{v_A} \cdot ln(\frac{m_E}{m_0}) + \vec{v_0}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-cf8abaf38a6a33f12eba3c787cfb23ad_l3.png)
Jetzt setzt du die Werte ein und berechnest die Geschwindigkeit:
![Rendered by QuickLaTeX.com \[\vec{v_E} = -20\frac{m}{s} \cdot ln(\frac{50000kg}{50000kg + 80000kg}) + 180\frac{m}{s} = 199,11\frac{m}{s}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2c687f6047fcbbdaf4b4bae1ec0ed933_l3.png)
Mit der Raketengleichung ermittelst du eine Endgeschwindigkeit von 199,11 m/s.
Arten von Raketenantrieben
Ein Raketenantrieb (oder Raketentriebwerk) ist das Bauteil einer Rakete, was durch den Ausstoß von Stützmasse zu einer Antriebskraft führt. Auf diese Art ist es den Raketen möglich, sich unabhängig von der Umgebung zu bewegen (z.B. Vakuum). In der Praxis gibt es eine Reihe von verschiedenen Raketenantrieben.
Aus diesem Grund geben wir dir im Anschluss einen Überblick über die verschiedenen Raketenantriebe:
- Feststofftriebwerk: Der Treibstoff und der Oxidator sind feste Materialien, die sich bereits zusammen im Treibstofftank befinden. Aus diesem Grund besitzen solche Antriebe einen einfachen Aufbau, weil der Treibstoff einfach im Treibstofftank verbrannt wird.
- Flüssigkeitstriebwerk: Der Treibstoff und der Oxidator sind flüssige Materialien, die getrennt in einzelnen Tanks vorliegen. Die einzelnen Komponenten werden anschließend zusammengeführt und verbrannt.
- Elektrostatischer Raketenantrieb: Hier wird der Treibstoff nicht verbrannt, sondern ionisiert. Anschließend wird der Treibstoff durch ein elektrisches Feld beschleunigt und aus der Rakete herausbefördert.
- Nuklearer Raketenantrieb: Der Treibstoff wird hier mithilfe von nuklearer Energie erhitzt und als Antrieb verwendet. Für die Erzeugung von nuklearer Energie wird die Kernspaltung oder die Kernfusion verwendet.
Energieumwandlung
In einem Raketenantrieb findet eine Energieumwandlung statt. Dabei wird zum Beispiel chemische Energie in kinetische Energie der Rakete umgewandelt. Schau dir unseren Beitrag zu Energieumwandlung an, um zu erfahren, welche anderen Arten von Energieumwandlung es gibt.