Video

Quiz

Hier geht's zum Video „Totale Differenzierbarkeit“

Hier geht's zum Video „Partielle Ableitungen“

Jacobi-Matrix

Wichtige Inhalte in diesem Video

Definition: Jacobi-Matrix bzw. Funktionalmatrix

Jacobi-Matrix als totale Ableitung

Beispiel 1 – Jacobi-Matrix berechnen

Die Jacobi-Matrix (oder Jacobimatrix aber nicht Jakobi-Matrix) ist nach dem deutschen Mathematiker Carl Gustav Jacob Jacobi benannt und ist von großer Bedeutung für die Differentialrechnung im Mehrdimensionalen. Man bezeichnet sie auch als Funktionalmatrix oder Ableitungsmatrix.

Du willst die Jacobi-Matrix noch schneller verstehen? Dann schau dir unser Video dazu an.

Inhaltsübersicht

Definition: Jacobi-Matrix bzw. Funktionalmatrix

im Videozur Stelle im Video springen

Sei $U\subset \mathbb{R}^n$ offen und f eine Funktion von folgender Form:

$f: U\rightarrow \mathbb{R}^m$

$(x_1,x_2, . . . ,x_n )\mapsto \left ( \begin{array}{r}f_1 (x_1,x_2, . . . ,x_n )\\ \vdots \\f_m (x_1,x_2, . . . ,x_n )\end{array} \right)$

Existieren alle partiellen Ableitungen der Komponentenfunktionen f_1, . . . ,f_m , so lautet die Jacobi-Matrix im Punkt $x_0\in U$ :

$J_f (x_0):=(\frac{\partial f_i}{\partial x_jx} (x_0))_(_i_=_1_,_._._._,_m_;_ j_=_1_,_._._._,_n_)=$

$\left ( \begin {array} {rrr} \frac{\partial f_1}{\partial x_1} (x_0) &\cdots &\frac{\partial f_1}{\partial x_n} (x_0 )\\ \vdots &\ddots &\vdots\\ \frac{\partial f_m}{\partial x_1} (x_0 )&\cdots &\frac{\partial f_m}{partial x_n} (x_0 )\end {array} \right)$

Häufig sieht man auch die Schreibweise Df(x_0 ) bzw. $\frac{\partial (f_1,. . . ,f_m)}{\partial (x_1,x_2, . . . ,x_n)} (x_0 )$ für die Jacobi-Matrix.

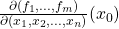Jacobi-Matrix Jacobimatrix Jakobi-Matrix — Jacobi-Matrix

Jacobi-Matrix als totale Ableitung

im Videozur Stelle im Video springen

Merke

Ist die betrachtete Funktion $f: \mathbb{R}^n\supset U \rightarrow \mathbb{R}^m$ im Punkt $x_0\in U$ total differenzierbar , so stellt die Jacobi-Matrix die totale Ableitung von f in x_0

x_0

dar.

Dies soll im Folgenden bewiesen werden:

Ist f in x_0 total differenzierbar, so gilt mit der totalen Ableitung A:

$f(x_0+h)=f(x_0)+A\cdot h+r(h)$ ,

wobei für die Restfunktion r(h) gilt:

$\lim\limits_{h\to\ 0} \frac{r(h)}{|h|} =0$

Hierbei ist A=(a_i_j)_(_i_=_1_,_._._._,_m_;_ j_=_1_,_._._._,_n_) eine Matrix und $h=\left ( \begin{array}{r} h_1\\ \vdots\\h_n\end {array} \right)$ ein n-dimensionaler Vektor.

Nun soll die i-te Komponente von f(x_0+h) betrachtet werden:

$f_i (x_0+h)=f_i (x_0 )+\sum\limits_{k=1}^n a_i_j\cdot h_k+r_j (h)$

Behält man in $h=\left ( \begin{array}{r} h_1\\ \vdots\\h_n\end{array} \right)$ nur die j-te Komponente ungleich null, wird daraus der Vektor $h_j e_j=\left ( \begin {array}{r} 0\\ \vdots\\h_j\\ \vdots \\0 \end{array}\right)$ und es ergibt sich:

$f_i (x_0+h_j e_j)=f_i (x_0)+a_i_j\cdot h_j+r_j (h_j e_j )$

Nun lässt sich damit und mit $\lim\limits_{h\to\ 0} \frac{r(h)}{|h|}=0$ die partielle Ableitung der i-ten Komponente von f nach x_j berechnen:

$\frac{\partial f_i}{\partial x_j}(x_0)=\lim\limits_{h_j\to\ 0} \frac {f_i (x_0+h_j e_j)-f_i (x_0)}{h_j} =a_i_j+\lim\limits_{h_j\to\ 0} \frac{r_j (h_j e_j )}{h_j} =a_i_j$

Es wurde also gezeigt, dass gilt:

$A=(a_i_j)_i_=_1_,_._._._,_m_;_j_=_1_,_._._._,_n=(\frac{\partial f_i}{\partial x_j} (x_0 ))_i_=_1_,_._._._,_m_;_j_=_1_,_._._._,_n=J_f (x_0)$

Das bedeutet gerade, dass die Jacobi-Matrix die totale Ableitung von f im Punkt x_0 ist.

Beispiel 1 – Jacobi-Matrix berechnen

im Videozur Stelle im Video springen

Die Berechnung der Jacobi-Matrix soll am Beispiel der Funktion

$f: \mathbb{R}^2\rightarrow \mathbb{R}^3$

$(x,y)\mapsto \left ( \begin{array}{r} f_1 (x,y)\\f_2 (x,y)\\f_3 (x,y)\end {array}\right )=\left ( \begin{array}{r} x^2+sin⁡(y)\\e^y+3\\2x^4\cdot y\end{array}\right )$

illustriert werden.
Für die Jacobi-Matrix werden die partiellen Ableitungen der drei Komponenten 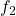f_1 , f_2 und f_3 nach x und y bestimmt. Diese lauten:

Jacobi-Matrix berechnen, Partielle Ableitungen, Jacobi Matrix Beispiel, Jacobi Matrix berechnen Beispiel — Jacobi-Matrix berechnen

Durch richtiges Anordnen dieser partiellen Ableitungen ergibt sich bereits die Jacobi-Matrix bzw. die Funktionalmatrix:

$J_f (x,y)=Df(x,y)=\left ( \begin {array}{rr} \frac{\partial f_1}{\partial x} (x,y) & \frac{\partial f_1} {\partial y} (x,y)\\\frac{\partial f_2}{\partial x} (x,y) & \frac{\partial f_2}{\partial y} (x,y)\\ \frac{\partial f_3}{\partial x} (x,y) & \frac{\partial f_3}{\partial y} (x,y) \end {array} \right )=\left ( \begin {array} {rr} 2x & cos⁡(y)\\0 & e^y\\ 8x^3\cdot y & 2x^4 \end {array} \right)$

Quiz zum Thema Jacobi-Matrix

Beispiel 2 – Jacobi-Matrix berechnen

Nun soll die Funktion

$\theta: \mathbb{R}^3\rightarrow \mathbb{R}^3$

$(r,\theta ,\varphi)\mapsto \left ( \begin {array} {r} x(r,\theta,\varphi)\\ y(r,\theta,\varphi)\\ z(r,\theta ,\varphi) \end{array} \right )= \left ( \begin {array} {r} r\cdot sin⁡(\theta)\cdot cos⁡(\varphi)\\r\cdot sin⁡(\theta )cdot sin⁡(\varphi)\\r\cdot cos⁡(\theta) \end{array}\right)$

betrachtet werden, welche eine Transformation der kartesischen in die Kugelkoordinaten beschreibt.

Die partiellen Ableitungen der einzelnen Komponenten lauten:

$\frac{\partial x}{\partial r} (r,\theta ,\varphi)= sin⁡(\theta) cos⁡(\varphi)$

$\frac{\partial x}{\partial \theta} (r,\theta ,\varphi )=r cos⁡(\theta)cos⁡(\varphi)$

$\frac c{\partial x}{\partial \varphi) (r,\theta,\varphi)=-r sin⁡(\theta) sin⁡(\varphi)$

$\frac{\partial y}{\partial r} (r,\theta,\varphi)= sin⁡(\theta) sin⁡(\varphi)$

$\frac{\partial y}{\partial\theta} (r,\theta ,\varphi)=r cos⁡(\theta)sin⁡(\varphi)$

$\frac{\partial y}{\partial \varphi} (r,\theta ,\varphi )=r sin⁡(\theta)cos⁡(\varphi)$

$\frac{\partial z}{\partial r} (r,\theta ,\varphi)=cos⁡(\theta)$

$\frac {\partial z}{\partial \theta} (r,\theta,\varphi)=-r sin⁡(\theta)$

$\frac{\partial z}{\partial \varphi} (r,\theta,\varphi)=0$

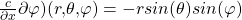
Die Jacobi-Matrix hat demzufolge folgende Form:

$J_f (r,\theta,\varphi)=\left ( \begin{array}{rrr} sin⁡(\theta) cos⁡(\varphi) & r cos⁡(\theta) cos⁡(\varphi) & -r sin⁡(\theta) sin⁡(\varphi)\\\\frac{sin⁡(\theta)sin⁡(\varphi) & r cos⁡(\theta)sin⁡(\varphi) & r sin⁡(\theta)cos⁡(\varphi)\\cos⁡(\theta) & -r sin⁡(\theta) & 0\end {array}\right)$

Da diese Jacobi-Matrix eine quadratische Matrix ist, lässt sich deren Determinante berechnen. Diese wird Jacobi-Determinante genannt. Sie spielt bei der Koordinatentransformation von Integralen eine wichtige Rolle. Im vorliegenden Fall lautet sie:

$det(J_f (r,\theta,\varphi))=r^2\cdot sin⁡(\theta)$

zur Videoseite: Jacobi-Matrix

Beliebte Inhalte aus dem Bereich Analysis

Partielle Ableitungen

Totale Differenzierbarkeit

Totales Differential

Gradient berechnen

Richtungsableitung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .