Sekante
Was ist die Definition einer Sekante? Wie sieht eine Sekantengleichung aus und wie kannst du von einer Sekante die Steigung berechnen? Hier bekommst du Antworten auf all diese Fragen!
Inhaltsübersicht
Sekante einfach erklärt
Eine Sekante ist eine Gerade, die eine geometrische Figur (z. B. einen Kreis ) oder einen Funktionsgraphen in zwei Punkten schneidet.
Sekanten begegnen dir also in der Geometrie, spielen aber auch in der Analysis eine wichtige Rolle. Dort werden sie oft durch Sekantengleichungen s(x) = mx + b mit der Sekantensteigung m beschrieben.
Übrigens: Der Name „Sekante“ kommt von dem lateinischen Wort „secare“. Das bedeutet „schneiden“.
Spitze! Jetzt kennst du schon die Definition einer Sekante! Du willst noch mehr darüber wissen? Dann schau doch auch mal in unser Video dazu rein!
Sekante — Kreis
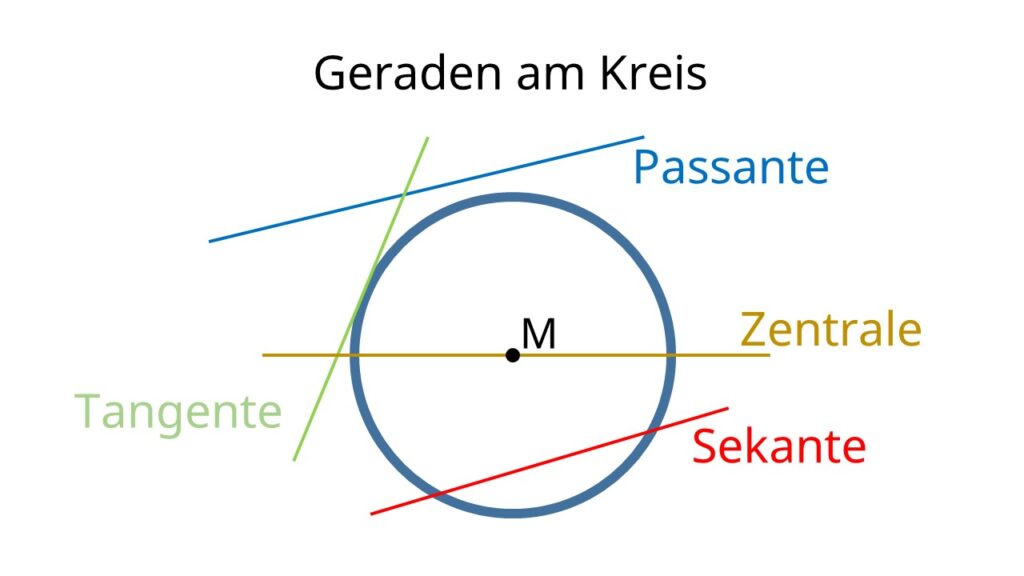
In der Geometrie ist die Sekante eine Gerade, die einen Kreis in genau zwei Punkten schneidet. Verläuft eine Sekante durch den Kreismittelpunkt M, nennst du sie auch Mittelpunktsgerade oder Zentrale.
Je nach Anzahl der Schnittpunkte unterscheidest du drei besondere Arten von Geraden am Kreis:
- Sekanten: 2 Schnittpunkte
- Tangenten : 1 Schnittpunkt (Berührpunkt)
- Passanten: kein Schnittpunkt
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Sekante — Funktionsgraph
Bei Funktionen sind Sekanten Geraden, die einen Funktionsgraphen in mindestens zwei Punkten P und Q schneiden.
Mathematiker beschreiben eine Sekante durch eine Sekantengleichung. Sie wird oft mit s(x) bezeichnet und hat — wie jede andere Geradengleichung — die Form:
s(x) = mx + b
Beispiel: s(x) = 2x – 1
Dabei bezeichnet m die Sekantensteigung (hier: 2) und b den y-Achsenabschnitt (hier: -1).
Schau dir gleich mal an einem Beispiel an, wie du damit eine Sekante berechnen kannst!
Sekanten berechnen
Wenn du zwei Punkte P ( x1 | y1 ) und Q ( x2 | y2 ) auf einem Funktionsgraphen gegeben hast, kannst du die Sekante durch P und Q berechnen. Du ermittelst dafür zuerst die Sekantensteigung m und den y-Achsenabschnitt b. Damit kannst du dann anschließend eine Sekantengleichung der Form s(x) = mx + b aufstellen. Probier das gleich mal mit den folgenden Punkten aus:
P ( 0 | -1 ) und Q ( 2 | 3 )
-
Sekante — Steigung berechnen
Für die Sekantensteigung m gibt es die Formel
m = (y2 – y1) : (x2 – x1)
Hier musst du jetzt nur noch die konkreten Werte aus den Punkten P ( 0 | -1 ) und Q ( 2 | 3 ) einsetzen:
m = (3 – (-1)) : (2 – 0) = 4 : 2 = 2
-
y-Achsenabschnitt berechnen
Um den y-Achsenabschnitt b zu bestimmen, brauchst du die Sekantensteigung m = 2 und einen Punkt ( x | y ) auf der Sekante, zum Beispiel P ( 0 | -1 ). m und P setzt du dann in die allgemeine Sekantengleichung s(x) = mx + b ein. Die y-Koordinate von P ist dabei der Funktionswert s(x). Hier bekommst du also:
-1 = 2 · 0 + b
Diese Gleichung lös du nun nach b auf:
b = -1
-
Sekantengleichung aufstellen
Wenn du dann m = 2 und b = -1 in s(x) = mx + b einsetzt, bekommst du die fertige Sekantengleichung s(x) = 2x – 1. Damit hast du die Sekante berechnet, die durch die Punkte P ( 0 | -1 ) und Q ( 2 | 3 ) verläuft. Super!
Vielleicht kennst du das Vorgehen schon von linearen Funktion . Es ist genau dasselbe Prinzip!
Übrigens: Manchmal sind die y-Werte der Punkte P und Q auf dem Funktionsgraphen nicht angegeben. Du kannst sie dann einfach berechnen, indem du die x-Werte in die Funktion einsetzt.
Zum Beispiel hast du die Funktion f(x) = x2 und die Punkte P ( 0 | f(0) ) und Q ( 2 | f(2) ). Durch das Einsetzen erhältst du: f(0) = 02 – 1 = -1 und f(2) = 22 -1 = 3. Jetzt kennst du die vollständigen Punkte P ( 0 | -1 ) und Q ( 2 | 3 ). Damit kannst du nun wie oben beschrieben die Sekante berechnen.
Sekanten einzeichnen
Bekommst du die Aufgabe, eine beliebige Sekante zu einer Funktion f einzuzeichnen , musst du nur darauf achten, dass sie die Funktion in zwei Punkten schneidet. Meistens hast du aber eine Gleichung der Form s(x) = mx + b für deine Sekante vorgegeben.
Schau dir das mal am Beispiel der Sekantengleichung s(x) = 2x -1 an.
-
Punkt auf y-Achse markieren
Den y-Achsenabschnitt b kannst du direkt aus der Sekantengleichung ablesen. Hier ist b = -1. Also machst du auf der y-Achse bei dem Wert -1 ein kleines Kreuz.
-
Sekantensteigung abtragen und Punkt markieren
Nun zeichnest du von dort aus ein Steigungsdreieck ein. Das heißt, du gehst von der markierten Stelle auf der y-Achse immer erstmal 1 Kästchen nach rechts. Die Steigung m gibt dir dann an, wie viele Kästchen du in dem Fall nach oben gehen musst. Hier sind es 2. Du landest damit bei dem Punkt ( 1 | 2 ). Dort setzt du dann ebenfalls ein Kreuz.
-
Sekante einzeichnen
Jetzt verbindest du nur noch das Kreuz auf der y-Achse mit dem Kreuz am Ende des Steigungsdreiecks durch eine gerade Linie. Und schon hast du die Sekante s(x) = 2x -1 eingezeichnet. Klasse!
Sekante — Die wichtigsten Fragen
-
Was ist eine Sekante?
Eine Sekante ist eine Gerade, die eine geometrische Figur (z. B. einen Kreis) oder einen Funktionsgraphen in zwei Punkten schneidet.
-
Welche wichtigen Geraden am Kreis gibt es?
Neben der Sekante gibt es noch Tangenten (ein Schnittpunkt), Passanten (kein Schnittpunkt) und die Zentrale (besondere Sekante durch den Kreismittelpunkt).
-
Wie sieht eine Sekantengleichung aus?
Die Sekantengleichung hat die Form einer linearen Funktion: s(x) = mx + b. Dabei ist m die Sekantensteigung und b der y-Achsenabschnitt.
-
Wie berechnet man die Sekantensteigung m?
Die Sekantensteigung m für eine Sekante durch P ( x1 | y1 ) und Q ( x2 | y2 ) berechnest du mit der Formel m = (y2 – y1) : (x2 – x1).
- Wie zeichnet man eine Sekante ein?
Beim Einzeichnen einer Sekante musst du beachten, dass sie den Funktionsgraphen in mindestens zwei Punkten schneidet. Hast du konkrete Schnittpunkte vorgegeben, gehst du so vor wie bei einer linearen Funktion.
Tangente
Jetzt kennst du die Sekante-Definition am Kreis und an Funktionen und weißt, wie du Sekanten berechnen kannst! Eine weitere wichtige Gerade ist die Tangente. Insbesondere in der Analysis besteht eine wichtige Verbindung zwischen Sekante und Tangente. Mehr über die Tangente erfährst du in diesem Video !