Video

Quiz

Polarkoordinaten

Wichtige Inhalte in diesem Video

Polarkoordinatensystem

Polarkoordinatendarstellung

Polarkoordinaten umrechnen

Polarkoordinaten in kartesische Koordinaten umrechnen

In diesem Artikel behandeln wir die Polarkoordinaten. Du erhältst zunächst eine Einführung und anschließend zeigen wir dir wie sie in kartesische Koordinaten umgerechnet werden können und umgekehrt. Zudem werden das Flächen- und Linienelement sowie die Einheitsvektoren thematisiert. Außerdem wird auf die Darstellung komplexer Zahlen in diesen Koordinaten eingegangen und die räumlichen Polarkoordinaten werden kurz dargestellt.

Um dir die viele Lesearbeit zu ersparen und das ganze Thema etwas anschaulicher aufzubereiten, haben wir für dich ein Video dazu erstellt.

Inhaltsübersicht

Ebene Polarkoordinaten Definition

Merke

In Polarkoordinaten wird ein Punkt der Ebene durch Angabe seines Abstands r zu einem vorgegebenen Koordinatenursprung (Pol) und durch Angabe eines Winkels $\phi$ bezüglich eines vorgegebenen Strahls durch den Pol (Polachse) beschrieben. Das Zahlenpaar $\left(r,\phi\right)$ wird als Polarkoordinaten der Ebene bezeichnet.

Polar- und kartesische Koordinaten können ineinander umgerechnet werden. Die Polarkoordinaten werden auch als Kreiskoordinaten bezeichnet.

Polarkoordinatensystem

im Videozur Stelle im Video springen

Das Polarkoordinatensystem wird durch seinen Koordinatenursprung, einen Punkt in der Ebene, den sogenannten Pol, und durch einen von diesem Pol fortlaufenden Strahl, der sogenannten Polachse, ausgezeichnet. Bezüglich dieses Punktes und des Strahls lassen sich dann die Polar- bzw. Kreiskoordinaten eines beliebigen Punktes in der Ebene angeben.

Polarkoordinatendarstellung

im Videozur Stelle im Video springen

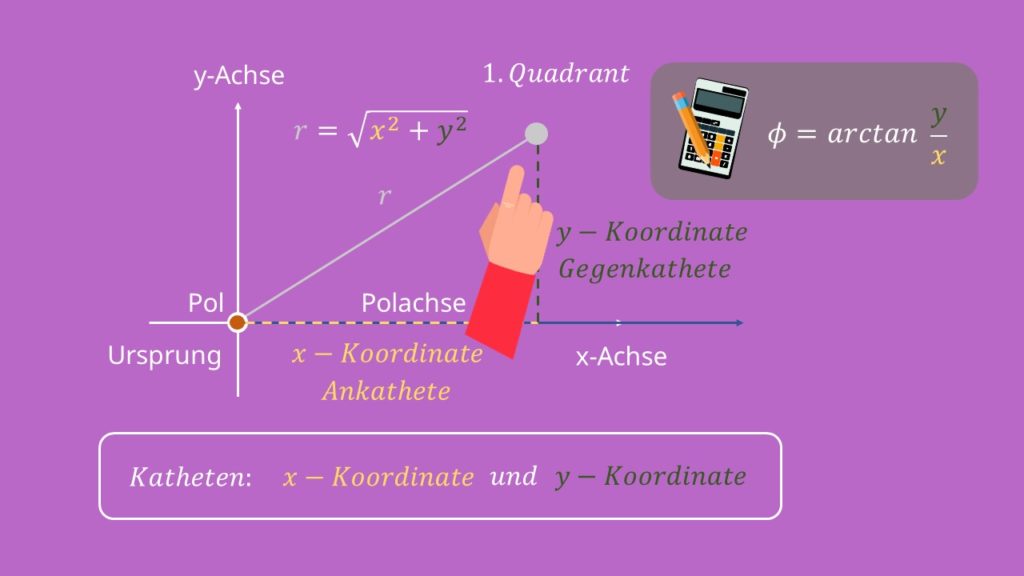
Soll ein beliebiger Punkt der Ebene in Polarkoordinaten beschrieben werden, so kann eine Strecke zwischen dem Punkt und dem Pol des Koordinatensystems betrachtet werden. Die erste Koordinate in der Polarkoordinatendarstellung ist der Abstand r des Punktes zum Pol, also die Länge der betrachteten Strecke. Dieser Abstand r wird auch als Radius bezeichnet.
Die zweite Koordinate $\phi$ ist gegeben durch den Winkel, den die betrachtete Strecke überstreicht, wenn sie im Uhrzeigersinn um den Pol bis zur Polachse gedreht wird. Dieser Winkel $\phi$ wird auch als Polarwinkel oder Azimut bezeichnet. Die Angabe der beiden Koordinaten r und $\phi$ eines Punktes der Ebene als Zahlenpaar $\left(r,\phi\right)$ wird als Polarkoordinatendarstellung bezeichnet.

Polarkoordinaten umrechnen

im Videozur Stelle im Video springen

Häufig kannst du bestimmte Rechnungen vereinfachen, wenn du vorher zwischen den Kreiskoordinaten und den kartesischen Koordinaten umrechnest. Im Folgenden zeigen wir dir beide Richtungen der Umrechnung.

Kartesische Koordinaten in Polarkoordinaten umrechnen

Um von den kartesischen Koordinaten in Polarkoordinaten umzurechnen, müssen aus den gegebenen Koordinaten $\mathbit{x}$ und $\mathbit{y}$ des kartesischen Systems der Radius r und der Polarwinkel $\phi$ berechnet werden. Der Einfachheit halber soll als Pol des Polarkoordinatensystems der Ursprung des kartesischen Systems und als Polachse die positive $\mathbit{x}$ -Achse gewählt werden.

Kartesische Koordinaten umrechnen Polarkoordinatensystem Polachse Polarkoordinaten — Kartesische Koordinaten umrechnen

Der Radius r lässt sich dann ganz einfach mithilfe des Satzes von Pythagoras berechnen:

$r=\sqrt{x^2+y^2}$

Die Bestimmung des Polarwinkels $\phi$ bringt hingegen ein paar Besonderheiten mit sich.

Zum einen kann der Winkel $\phi$ für den Fall, dass r=0 gilt, jeden beliebigen Wert annehmen. In diesem Fall wird meist $\phi=0$ verwendet.

Zum anderen ist der Winkel auch für $r\neq0$ nicht eindeutig definiert. Wird nämlich zu einem gegebenen Winkel der Wert $2\pi$ addiert, so wird durch den dadurch erhaltenen Winkel derselbe Punkt in der Ebene beschrieben. Um eine eindeutige Transformationsvorschrift zu erhalten wird die Angabe des Winkels auf ein halboffenes Intervall der Länge $\mathbf{2}\mathbit{\pi}$ wie beispielsweise das Intervall $\left[0,2\pi\right)$ beschränkt.

Für den ersten Quadranten lässt sich der Winkel dann ganz einfach mithilfe des Arkustangens berechnen. Für die anderen Quadranten muss jeweils noch ein Wert dazu addiert werden. Es ergibt sich folgende Fallunterscheidung:

$x>0,\ y\geq0$ $\phi=arctan{\frac{y}{x}}$

$x>0,\ y<0$ $\phi=arctan{\frac{y}{x}}+2\pi$

x<0 $\phi=arctan{\frac{y}{x}}+\pi$

Für den Fall, dass x=0 gilt, ergeben sich folgende Winkel:

$x=0,\ y>0$ $\phi=90°$
$x=0,\ y<0$ $\phi=270°$

Arkustangens berechnen Polarkoordinaten Polachse Kartesische Koordinaten — Arkustangens berechnen

Polarkoordinaten in kartesische Koordinaten umrechnen

im Videozur Stelle im Video springen

Die Umrechnung der Polarkoordinaten in kartesischen Koordinaten folgt hingegen einfacheren Rechenvorschriften. Es gilt:

$x=r\cdot cos\left(\phi\right)$
$y=r\cdot sin\left(\phi\right)$

Flächenelement

Mit den Transformationsgleichungen $x=r\cdot cos\left(\phi\right)$ und $y=r\cdot sin\left(\phi\right)$ gilt für die Funktionaldeterminante in Kreiskoordinaten:

$det\frac{\partial\left(x,y\right)}{\partial\left(r,\phi\right)}=det\left(\begin{matrix}\frac{\partial x}{\partial r}&\frac{\partial x}{\partial\phi}\\\frac{\partial y}{\partial r}&\frac{\partial y}{\partial\phi}\\\end{matrix}\right)=det\left(\begin{matrix}cos\left(\phi\right)&-r\cdot s i n\left(\phi\right)\\sin\left(\phi\right)&r\cdot c o s\left(\phi\right)\\\end{matrix}\right)=r\cdot cos^2\left(\phi\right)+r\cdot sin^2\left(\phi\right)=r$

Somit ergibt sich für das Flächenelement dA:

$dA=dx\ dy=det\frac{\partial\left(x,y\right)}{\partial\left(r,\phi\right)}dr\ d\phi=r\ dr\ d\phi$

Linienelement

Ebenso ergibt sich aus den genannten Transformationsgleichungen $\ x=r\cdot cos\left(\phi\right)$ und $y=r\cdot sin\left(\phi\right)$ folgender Zusammenhang:

$dx=\ cos\left(\phi\right)\ dr-r\cdot sin\left(\phi\right)\ d\phi$
$dy=sin\left(\phi\right)\ dr+r\cdot cos\left(\phi\right)\ d\phi$

Da in den kartesischen Koordinaten der Zusammenhang

ds^2=dx^2+dy^2

gilt, folgt mit obigen Gleichungen in Kreiskoordinaten für das Linienelement ds:

$ds^2=\left(cos\left(\phi\right)\ dr-r\cdot s i n\left(\phi\right)\ d\phi\right)^2+\left(sin\left(\phi\right)\ dr+r\cdot c o s\left(\phi\right)\ d\phi\right)^2$

Durch Vereinfachen ergibt sich:

$ds^2=dr^2+r^2\ d\phi^2$

Einheitsvektoren

Mit dem Richtungsvektor $\vec{r}=\left(\begin{matrix}r\cdot c o s\left(\phi\right)\\r\cdot s i n\left(\phi\right)\\\end{matrix}\right)$ gilt für die Basisvektoren bzw. die Einheitsvektoren $\vec{e_r}$ und $\vec{e_\phi}$ in Kreiskoordinaten:

$\vec{e_r}=\frac{1}{\left|\frac{\partial\vec{r}}{\partial r}\right|}\cdot\frac{\partial\vec{r}}{\partial r}=\frac{1}{\sqrt{cos^2\left(\phi\right)+sin^2\left(\phi\right)}}\cdot\left(\begin{matrix}cos\left(\phi\right)\\sin\left(\phi\right)\\\end{matrix}\right)=\left(\begin{matrix}cos\left(\phi\right)\\sin\left(\phi\right)\\\end{matrix}\right) \vec{e_\phi}=\frac{1}{\left|\frac{\partial\vec{r}}{\partial\phi}\right|}\cdot\frac{\partial\vec{r}}{\partial\phi}=\frac{1}{\sqrt{r^2\cdot s i n^2\left(\phi\right)+r^2\cdot c o s^2\left(\phi\right)}}\cdot\left(\begin{matrix}-r\cdot s i n\left(\phi\right)\\r\cdot c o s\left(\phi\right)\\\end{matrix}\right)=\left(\begin{matrix}-sin\left(\phi\right)\\cos\left(\phi\right)\\\end{matrix}\right)$

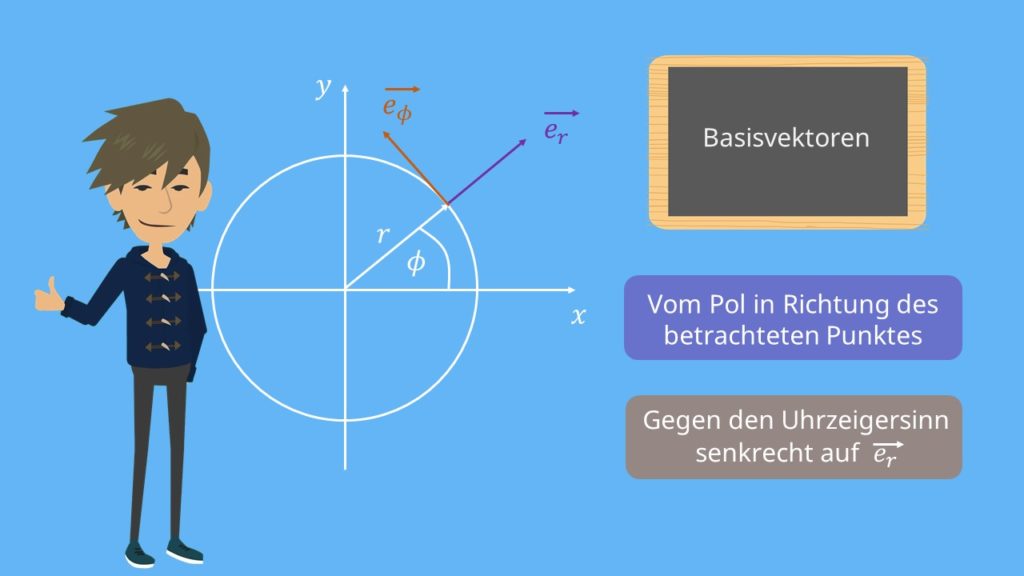
Die Einheitsbasisvektoren in Kreiskoordinaten sind also davon abhängig, welcher Punkt der Ebene betrachtet wird. Während der eine Einheitsvektor $\vec{e_r}$ vom Pol in Richtung des betrachteten Punktes zeigt, steht der zweite Einheitsvektor $\vec{e_\phi}$ gegen den Uhrzeigersinn senkrecht auf dem Vektor $\vec{e_r}$ .

Basisvektoren Pol Polkoordinaten — Basisvektoren

Geschwindigkeit und Beschleunigung in Polarkoordinaten

Mit den Einheitsvektoren lässt sich eine Bewegung in Kreiskoordinaten in eine radiale und eine transversale Komponente zerlegen. Es gilt nämlich für die Geschwindigkeit $\dot{\vec{r}}$ :

$\dot{\vec{r}}=\frac{d\vec{r}}{dt}=\frac{d}{dt}\left(\begin{matrix}r\cdot c o s\left(\phi\right)\\r\cdot s i n\left(\phi\right)\\\end{matrix}\right)=\left(\begin{matrix}\dot{r}\cdot c o s\left(\phi\right)-r\cdot s i n\left(\phi\right)\cdot\dot{\phi}\\\dot{r}\cdot s i n\left(\phi\right)+r\cdot c o s\left(\phi\right)\cdot\dot{\phi}\\\end{matrix}\right)=\dot{r}\cdot\vec{e_r}+r\cdot\dot{\phi}\cdot\vec{e_\phi}$

Analog gilt für die Beschleunigung $\ddot{\vec{r}}$ :

$\ddot{\vec{r}}=\frac{d\dot{\vec{r}}}{dt}=\left(\begin{matrix}\ddot{r}\cdot c o s\left(\phi\right)-\dot{r}\cdot s i n\left(\phi\right)\cdot\dot{\phi}-(\dot{r}\cdot s i n\left(\phi\right)+r\cdot c o s\left(\phi\right)\cdot\dot{\phi})\cdot\dot{\phi}-r\cdot s i n\left(\phi\right)\cdot\ddot{\phi}\\\ddot{r}\cdot s i n\left(\phi\right)+\dot{r}\cdot c o s\left(\phi\right)\cdot\dot{\phi}+(\dot{r}\cdot c o s\left(\phi\right)-r\cdot s i n\left(\phi\right)\cdot\dot{\phi})\cdot\dot{\phi}+r\cdot c o s\left(\phi\right)\cdot\ddot{\phi}\\\end{matrix}\right)$

Durch Zusammenfassen ergibt sich:

$\ddot{\vec{r}}=\left(\ddot{r}-r\cdot{\dot{\phi}}^2\right)\cdot\vec{e_r}+\left(2\cdot\dot{r}\cdot\dot{\phi}+r\cdot\ddot{\phi}\right)\cdot\vec{e_\phi}$

Polarkoordinaten und komplexe Zahlen

Eine komplexe Zahl $z\in\mathbb{C}$ kann mit ihrem Realteil $Re\left(z\right)$ und ihrem Imaginärteil $Im\left(z\right)$ auf folgende Art und Weise dargestellt werden:

$z=Re\left(z\right)+i\cdot Im\left(z\right)$

Dies kommt einer Darstellung der komplexen Zahl in kartesischen Koordinaten gleich, wobei der Realteil $Re\left(z\right)$ der x-Koordinate und der Imaginärteil $Im\left(z\right)$ der y-Koordinate entspricht. Eine andere Darstellung der Zahl gleicht dann einer Darstellung in Kreiskoordinaten:

$z=\left|z\right|\cdot e^{i\phi}$

Mit der Eulerschen Formel gleicht dies folgender Schreibweise:

$z=\left|z\right|\cdot\left(cos\left(\phi\right)+i\cdot s i n\left(\phi\right)\right)=\left|z\right|\cdot cos\left(\phi\right)+i\cdot\left|z\right|\cdot sin\left(\phi\right)$

Durch Vergleich mit der Darstellung der komplexen Zahl in kartesischen Koordinaten ergeben sich wieder die bekannten Transformationsgleichungen:

$Re\left(z\right)=\left|z\right|\cdot cos\left(\phi\right)$

$Im\left(z\right)=\left|z\right|\cdot sin\left(\phi\right)$

Räumliche Polarkoordinaten

Werden die Kreiskoordinaten um eine dritte Koordinate ergänzt, so ergeben sich sogenannte räumliche Polarkoordinaten. Hierzu zählen Zylinderkoordinaten oder die Kugelkoordinaten.

zur Videoseite: Polarkoordinaten

Beliebte Inhalte aus dem Bereich Analysis

Polarkoordinaten

Zylinderkoordinaten

Kugelkoordinaten

Satz von Stokes

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .