Differenzenquotient
In diesem Artikel erklären wir dir, was der Differenzenquotient ist und in welchem Zusammenhang er mit dem Differentialquotienten steht. Dafür verwenden wir viele Grafiken und Beispiele.
Du möchtest gern alles Wichtige über den Differenzenquotient erfahren, aber bist eher der audiovisuelle Lern-Typ? Kein Problem! Schau dir einfach unser Video dazu an.
in zwei Punkten 
und 
schneidet, eine sogenannte Sekante.Mittlere Änderungsrate Differenzenquotient
Graphisch sieht die beschriebene Situation folgendermaßen aus:
Du hast also eine Funktion 
und eine Sekante gegeben, die den Graphen in zwei Punkten 
und 
schneidet. Dein Ziel ist es die Steigung dieser Sekante zu bestimmen. Dafür zeichnest du ein sogenanntes Steigungsdreieck unterhalb der Sekante ein.
Für deren Steigung musst du nun die Höhe des Dreiecks 
durch die Länge des Dreiecks 
teilen, das heißt
Für die Höhe siehst du dir den y-Abschnitt des Dreiecks an. Da die Ecken des Dreiecks auf den Punkten und liegen, berechnest du ihn folgendermaßen:
Das Gleiche machst du auch für die Länge beziehungsweise den x-Abschnitt des Dreiecks und erhältst so:
Nun setzt du deine Ergebnisse in die Formel des Steigungsdreiecks ein und bekommst damit die Definition des Differenzenquotient, auch mittlere Änderungsrate genannt:
Beispiel 1
Betrachten wir ein theoretisches Differenzenquotient Beispiel und zwar sollst du die mittlere Änderungsrate der Funktion
zwischen 
und 
bestimmen. Entsprechend der Differenzenquotient Formel berechnest du also
Beispiel 2
Angenommen du fährst mit dem Zug in den Urlaub und die Funktion beschreibt den Weg, den du während deiner Fahrt zurückgelegt hast.
Das heißt auf der x-Achse des Koordinatensystems wird die Zeit in Stunden und auf der y-Achse die Strecke in Kilometern aufgetragen.
Nach einer halben Stunde fährst du an Augsburg vorbei. Bis hierhin hast du bereits eine Strecke von 10km zurückgelegt. Es gilt also:
Nach insgesamt eineinhalb Stunden kannst du München sehen. Der Zug ist bis jetzt 80km gefahren, was bedeutet:
Nun möchtest du gerne die mittlere Geschwindigkeit des Zuges auf der Strecke Augsburg-München wissen und zeichnest eine Sekante mit den Schnittpunkten 
und 
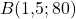ein.
Für die Geschwindigkeit rechnest du nun Strecke durch Zeit:
Das heißt, du berechnest die Steigung der Sekante, also das eingezeichnete Steigungsdreieck, aus, nämlich:
Auf der Strecke zwischen Augsburg und München hatte der Zug somit eine durchschnittliche Geschwindigkeit von 70km/h.
In diesem Fall hast du also mit dem Differenzenquotient die mittlere Änderungsrate zwischen 
und 
ausgerechnet.
Grenzwert des Differenzenquotienten
Im Folgenden sehen wir uns an, was passiert, wenn du beim Differenzenquotient Berechnen den Wert 
immer mehr an den Wert 
annäherst.
Wie du in der Grafik siehst, wird die Sekante zur Tangente, wenn gegen läuft. Genauer gesagt, siehst du hier den Übergang: Differenzenquotient Differentialquotient.
Das heißt der Grenzwert 
des Differenzenquotient ergibt den sogenannten Differentialquotienten:
welcher die Steigung der Tangente im Punkt berechnet.
Übersicht Differentialrechnung
Du kennst nun den Zusammenhang zwischen dem Differenzenquotient und dem Differentialquotient. Eine andere Interpretation des Differentialquotienten ist die h Methode .
Die folgende Tabelle gibt dir nochmal eine Übersicht über diese drei elementaren Begriffe der Differentialrechnung.
| Begriff | Formel | Bedeutung |
| Differenzenquotient |  |
Sekantensteigung |
| Differentialquotient |  |
Tangentensteigung |
| h Methode |  |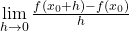
Tangentensteigung |
