Ableiten
Wie kannst du verschiedene Funktionen ableiten? Und was musst du dabei beachten? Das erfährst du hier und in unserem Video !
Inhaltsübersicht
Ableiten einfach erklärt
Beim Ableiten findest du die Steigung einer Funktion in bestimmten Punkten heraus. So kannst du berechnen, in welchen Punkten eine Funktion steigt (Ableitung größer 0), fällt (Ableitung kleiner 0) oder gleich bleibt (Ableitung gleich 0). Die Ableitung bezeichnest du mit f'(x).
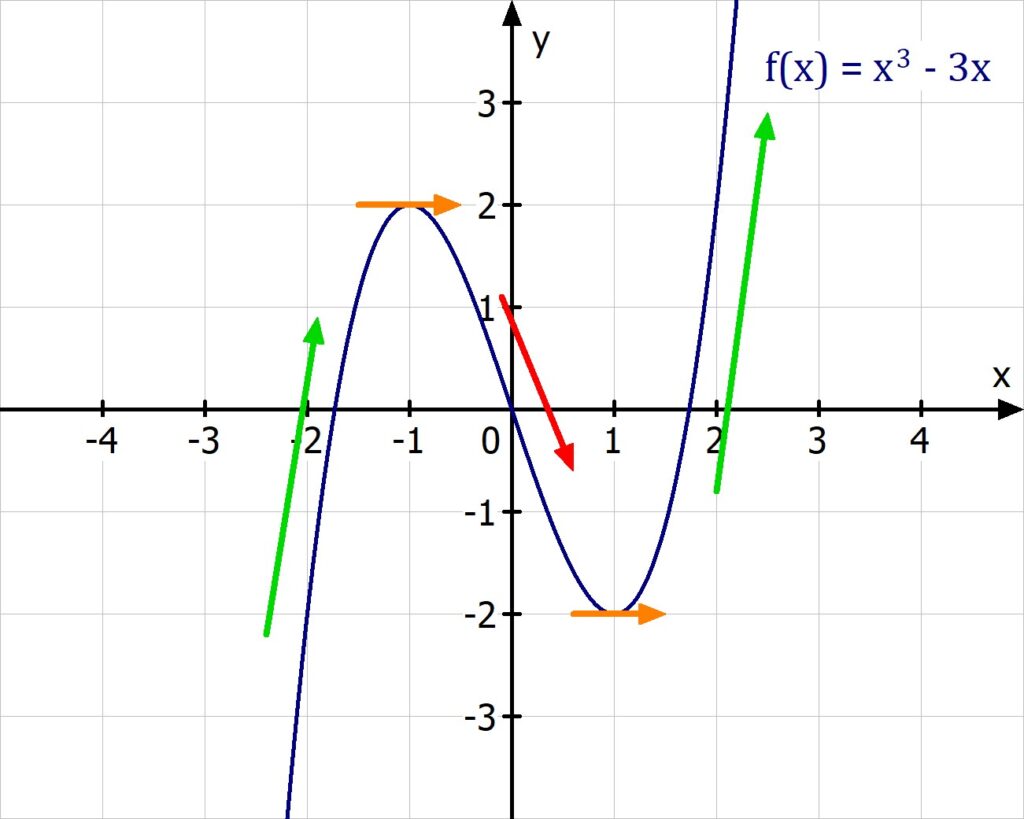
Beispiel: Die Ableitung von f(x) = x3 – 3x ist f'(x) = 3x2 – 3. f'(0) zum Beispiel ist dann -3, also kleiner 0. Am Graphen siehst du deshalb, dass die Funktion an x = 0 fällt:
In einer Kurvendiskussion kannst du durch Ableiten insbesondere herausfinden, wo die Extrempunkte (Hoch- und Tiefpunkte ) einer Funktion liegen.
Für unterschiedliche Funktionen brauchst du ganz unterschiedliche Regeln zum Ableiten. Die wichtigsten siehst du hier auf einen Blick:
| Funktion f(x) | Ableitung f'(x) |
| Polynome | |
| f(x) = Zahl | f'(x) = 0 |
| f(x) = mx + t | f'(x) = m |
| f(x) = x2 | f'(x) = 2x |
| f(x) = xp | f'(x) = p • xp-1 |
| e-Funktion und ln | |
| f(x) = ex | f'(x) = ex |
| f(x) = ln(x) | f'(x) = 
|
| Sinus und Cosinus | |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
| Wurzeln und Brüche | |
f(x) = 
|
f'(x) = 
|
f(x) = 
|
f'(x) = 
|
Durch Ableiten findest du die Tangentensteigung in einem bestimmten Punkt eines Graphen heraus. Ist die Ableitung positiv, dann steigt die Funktion. Ist sie negativ, so fällt der Graph. Ableiten funktioniert bei jeder Funktion unterschiedlich und nach bestimmten Regeln.
Graphisches Ableiten
Beim graphischen Ableiten schaust du dir den Graphen deiner Funktion f(x) an und zeichnest daraus (ohne zu rechnen!) den Graphen der Ableitung f'(x). Dabei gehst du so vor:
- Die Extremstellen (E) der Funktion werden die Nullstellen (N) der Ableitung (hier: -1 und 1)
- Die Wendestellen (W) der Funktion werden die Extremstellen (E) der Ableitung (hier 0)
Die so entstandenen Nullstellen und Extrempunkte verbindest du dann zu einer Kurve — dem Graphen deiner Ableitung.
Du kannst dir graphisches Ableiten mithilfe einer Tabelle und der Eselsbrücke „NEW“ ganz leicht merken.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Graphisches Ableiten
Für die Extremstellen E, die Nullstellen N und die Wendestellen W gilt:
| f(x) | N | E | W | |
| f'(x) | N | E | W |
Ableiten verschiedener Funktionen
Oft brauchst du nicht nur graphisches Ableiten, sondern musst die Ableitung berechnen. Je nach Funktion gehst du dabei unterschiedlich vor. Im Folgenden erfährst du die wichtigsten Regeln.
Ableiten ganzrationaler Funktionen
Eine ganzrationale Funktion besteht aus Zahlen und x mit verschiedenen Hochzahlen. Ganzrationale Funktionen sind zum Beispiel
- 3x + 5
- x2 – 5x + 3
- x4
Zum Ableiten verwendest du die Potenzregel , die Faktorregel und die Summenregel .
- Potenzregel: Um x2, x3, x4… abzuleiten, ziehst du den Exponenten nach vorne und erniedrigst die Hochzahl danach um eins:
f(x) = x3 → f'(x) = 3 • x3-1 = 3x2
- Faktorregel: Steht vor x2, x3, x4… eine Zahl, zum Beispiel bei 2x3, dann multiplizierst du den vorgezogenen Exponenten mit der Zahl:
f(x) = 2x3 → f'(x) = 2 • 3 • x3-1 = 6x2
- Summenregel: Wenn du eine Summe ableitest, zum Beispiel x2 + 5x, kannst du jeden Teil einzeln ableiten:
f(x) = x2 + 5x → f'(x) = 2x + 5
Zwei Ableitungen solltest du dir besonders gut merken:
- x abgeleitet ergibt immer 1: f(x) = x → f'(x) = 1
- eine Zahl c abgeleitet ergibt immer 0: f(x) = c → f'(x) = 0
Ableiten von e-Funktion und ln-Funktion
Die e-Funktion ex kannst du ganz leicht ableiten. Es gilt nämlich:
f(x) = ex → f'(x) = ex
Für die ln-Funktion kannst du dir merken:
f(x) = ln(x) → f'(x) = 
Wenn du komplizierte e-Funktionen und ln-Funktionen ableiten sollst, brauchst du oft die Kettenregel . Du möchtest dazu mehr wissen? Dann schau dir unsere Videos zu Ableiten der e-Funktion und zum Ableiten vom ln an.
Ableiten von Sinus und Cosinus
Auch die Ableitung von Sinus und Cosinus ist gar nicht schwer:
f(x) = sin(x) → f'(x) = cos(x)
f(x) = cos(x) → f'(x) = – sin(x)
Wenn im Sinus oder im Cosinus nicht nur ein x vorkommt, brauchst du zum Ableiten oft die Kettenregel. Wie du dann genau vorgehst, erfährst du hier .
Ableiten der Wurzel
Die Wurzelfunktion abgeleitet ergibt:
f(x) =  → f'(x) =
→ f'(x) = 
Steht unter der Wurzel mehr als nur ein x, so brauchst du noch weitere Regeln. Alles Wichtige dazu erfährst du hier !
Ableitungsregeln
Bei vielen Funktionen brauchst du zum Ableiten bestimmte Regeln, die sogenannten Ableitungsregeln .
Produktregel
Du Produktregel verwendest du, wenn deine Funktion ein Produkt ist, also ein Mal enthält, wie hier:
f(x) = x2 • sin(x)
Den ersten Faktor des Produkts nennst du dann u(x), also hier u(x) = x2, und den zweiten Faktor nennst du v(x), also v(x) = sin(x). Dann gilt die Produktregel:
f'(x) = u(x) • v'(x) + u'(x) • v(x)
In deinem Beispiel bildest du also zuerst die Ableitungen von u und v:
- u(x) = x2 → u'(x) = 2x
- v(x) = sin(x) → v'(x) = cos(x)
Mithilfe der Produktregel kannst du dann die Ableitung f bilden:
f'(x) = x2 • cos(x) + 2x • sin(x)
Das ging dir zu schnell? Dann kannst du hier in Ruhe mit der Produktregel das Ableiten üben!
Quotientenregel
Mit der Quotient enregel kannst du Brüche ableiten, zum Beispiel
![Rendered by QuickLaTeX.com \[f(x) = \frac{\textcolor{blue}{x^2}}{\textcolor{red}{\sin(x)}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9b9fa04d288b277a1abe1d7a16385166_l3.png)
Den oberen Teil (Zähler) nennst du g(x), hier also g(x) = x2, und den unteren Teil (Nenner) h(x). Hier ist also h(x) = sin(x). Dann ist die Ableitung allgemein:
![Rendered by QuickLaTeX.com \[ f'(x) = \frac{\textcolor{red}{h(x)}\cdot \textcolor{teal}{g'(x)} - \textcolor{orange}{h'(x)} \cdot \textcolor{blue}{g(x)}}{\textcolor{red}{h(x)}^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e9a69d0bf4ee21b0a22e1ee795aa2b57_l3.png)
Im Beispiel suchst du also zuerst die Ableitungen von g und h:
- g(x) = x2 → g'(x) = 2x
- h(x) = sin(x) → h'(x) = cos(x)
![Rendered by QuickLaTeX.com \[ f'(x) = \frac{\textcolor{red}{\sin(x)}\cdot \textcolor{teal}{2x} - \textcolor{orange}{\cos(x)} \cdot \textcolor{blue}{x^2}}{\textcolor{red}{\sin(x)}^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f377fb83582d6860bb49e7fa5e877c9f_l3.png)
Wenn du noch mehr mit der Quotientenregel das Ableiten üben willst, dann schau hier vorbei!
Kettenregel
Die Kettenregel verwendest du, wenn eine Funktion innerhalb einer anderen steht („verkettete“ Funktionen). Hier siehst du ein Beispiel:
h(x) = sin(3x + 5)
Die Funktion f(x) = 3x + 5 steht innerhalb der Sinusfunktion. Die äußere Funktion kannst du mit g(y) = sin(y) bezeichnen. Dann ist die Ableitung von h(x):
h'(x) = g‘(f(x)) • f'(x)
Im Beispiel ist f(x) = 3x + 5 und g(y) = sin(y). Somit ist f'(x) = 3 und g'(y) = cos(y). Also erhältst du:
h'(x) = cos(3x + 5) • 3
Viele weitere Beispiele zur Kettenregel findest du hier !
Ableiten — häufigste Fragen
(ausklappen)
Ableiten — häufigste Fragen
(ausklappen)-
Wie entscheide ich, ob ich die Produktregel oder die Kettenregel brauche?Du brauchst die Produktregel bei einem echten Produkt
 und die Kettenregel bei einer „Funktion in der Funktion“
und die Kettenregel bei einer „Funktion in der Funktion“  . Erkenne zuerst die äußere Rechenoperation: Mal bedeutet Produkt, „etwas in Klammern“ als Argument bedeutet Verkettung. Zum Beispiel ist
. Erkenne zuerst die äußere Rechenoperation: Mal bedeutet Produkt, „etwas in Klammern“ als Argument bedeutet Verkettung. Zum Beispiel ist  eine Produktregel, aber
eine Produktregel, aber  eine Kettenregel.
eine Kettenregel.
-
Welche Fehler passieren oft bei der Kettenregel?Häufige Fehler bei der Kettenregel sind: die innere Ableitung
 wird vergessen, die äußere Funktion wird falsch abgeleitet oder die Klammer wird nicht als Ganzes eingesetzt. Beispiel: Bei
wird vergessen, die äußere Funktion wird falsch abgeleitet oder die Klammer wird nicht als Ganzes eingesetzt. Beispiel: Bei  ist falsch
ist falsch  , richtig ist
, richtig ist  , weil
, weil  .
.
-
Wie leite ich ln von einer Klammer richtig ab?
 von einer Klammer leitest du mit der Kettenregel ab:
von einer Klammer leitest du mit der Kettenregel ab:  . Das liegt daran, dass die äußere Ableitung von
. Das liegt daran, dass die äußere Ableitung von  gleich
gleich  ist und dann mit der inneren Ableitung multipliziert wird. Zum Beispiel gilt
ist und dann mit der inneren Ableitung multipliziert wird. Zum Beispiel gilt  .
.
-
Wie leite ich e hoch einer Klammer richtig ab?
 hoch einer Klammer leitest du mit der Kettenregel ab:
hoch einer Klammer leitest du mit der Kettenregel ab:  . Die äußere Funktion bleibt also
. Die äußere Funktion bleibt also  , und dazu kommt die Ableitung der Klammer als Faktor. Zum Beispiel ist
, und dazu kommt die Ableitung der Klammer als Faktor. Zum Beispiel ist  .
.
-
Wie leite ich eine Wurzel mit einer Klammer darunter ab?Eine Wurzel mit Klammer darunter leitest du als
 mit der Kettenregel ab:
mit der Kettenregel ab:  . Dabei wird die innere Ableitung
. Dabei wird die innere Ableitung  leicht vergessen. Zum Beispiel gilt
leicht vergessen. Zum Beispiel gilt  .
.
Kurvendiskussion
Prima! Jetzt kannst du jede Funktion ableiten und bist bereit für die Kurvendiskussion! Dabei spielt Ableiten nämlich eine entscheidende Rolle. Schau dir gleich an, wie eine Kurvendiskussion funktioniert!