Bestimmtes und unbestimmtes Integral

Bestimmtes Integral berechnen

(01:44)

Bestimmtes Integral berechnen Beispiel

Bestimmtes Integral berechnen – Besonderheiten

Unbestimmtes Integral

Unbestimmtes Integral berechnen Beispiele

(00:49)

Das bestimmte und unbestimmte Integral spielen eine große Rolle in der Integralrechnung. Worin ihr Unterschied besteht und wie du sie berechnest, erfährst du hier und in unserem Video !

Inhaltsübersicht

Bestimmtes und unbestimmtes Integral einfach erklärt

Der Unterschied zwischen einem bestimmten und einem unbestimmten Integral besteht darin, dass das bestimmte Integral Integrationsgrenzen hat.

$\int\limits_{\textcolor{red}{a}}^{\textcolor{red}{b}} f(x) \, dx$

Beim Berechnen eines bestimmten Integrals kommt deshalb eine konkrete Zahl heraus. Die gibt dir den orientierten (positiven oder negativen) Flächeninhalt unter dem Graphen an.

unbestimmtes Integral, bestimmtes Integral, unbestimmte Integrale, bestimmtes Integral berechnen, bestimmte Integral, Berechnung unbestimmter Integrale, Graph, Funktion, Fläche, Flächeninhalt, Flächenbilanz, Koordinatensystem, Funktionsgleichung, Parabel, Intervall — Flächeninhalt unter einer Funktion

Ein unbestimmtes Integral hingegen hat keine Integralgrenzen.

$\int f(x) \, dx$

Du berechnest es, indem du die sogenannte Stammfunktion von f(x) ermittelst. Davon gibt es immer unendlich viele. Die Menge aller Stammfunktionen nennst du dann unbestimmtes Integral.

Bestimmtes Integral berechnen

(01:44)

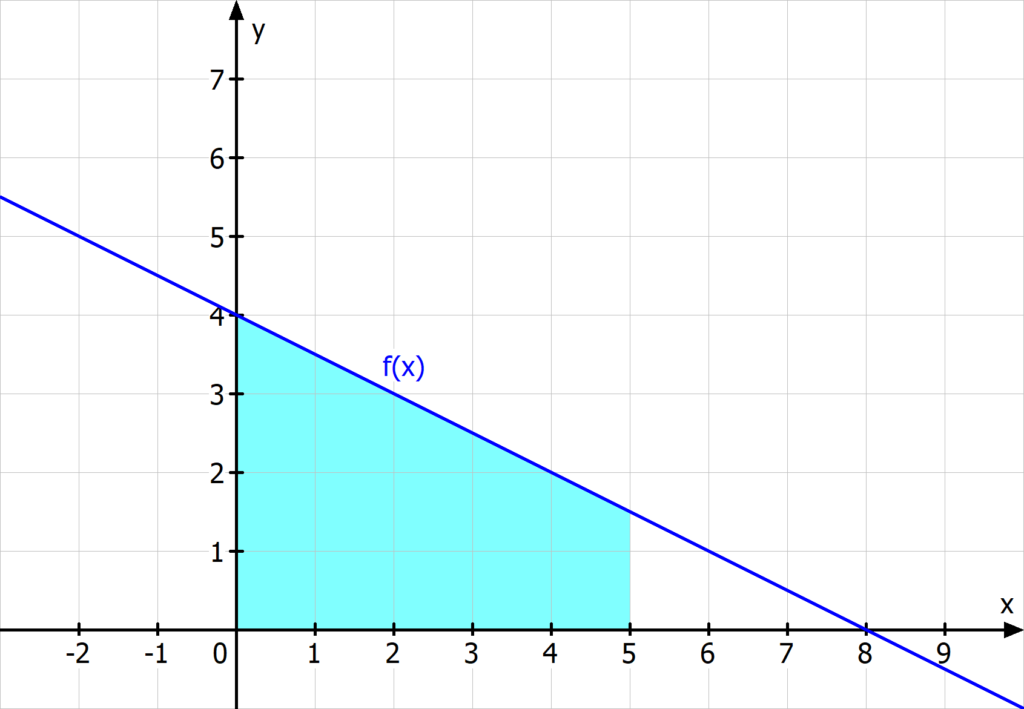
Ein bestimmtes Integral kannst du konkret berechnen. Schau dir das am besten gleich an einem Beispiel an. Berechne das bestimmte Integral:

$\int \limits_0^5 -\frac{1}{2}x+4 \, dx$

Schritt 1: Berechne die Stammfunktion F(x). Sie lautet hier:

$F(x) = -\frac{1}{4}x^2+4x$

Schritt 2: Schreibe F(x) in eckige Klammern und dahinter die Integrationsgrenzen.

$\int \limits_{\textcolor{orange}{0}}^{\textcolor{red}{5}} -\frac{1}{2}x+4 \, dx = \biggl[-\frac{1}{4}x^2+4x\biggr]\limits_{\textcolor{orange}{0}}^{\textcolor{red}{5}}$

Schritt 3: Berechne das bestimmte Integral. Rechne dazu:

F(obere Grenze) – F(untere Grenze), also

$\int \limits_{\textcolor{orange}{0}}^{\textcolor{red}{5}} -\frac{1}{2}x+4 \, dx = \biggl[-\frac{1}{4}x^2+4x\biggr]\limits_{\textcolor{orange}{0}}^{\textcolor{red}{5}} = (-\frac{1}{4} \cdot {\textcolor{red}{5}}^2+4\cdot {\textcolor{red}{5}}) - (-\frac{1}{4}\cdot {\textcolor{orange}{0}}^2+4\cdot {\textcolor{orange}{0}}) = 13,75$

Damit weißt du, dass der orientierte Flächeninhalt zwischen der x-Achse im Intervall [0, 5] und dem Graphen 13,75 groß ist.

Integral Flächeninhalt — Beispiel 1: Berechnung eines bestimmten Integrals

In deiner Rechnung hast du den sogenannten Hauptsatz der Differential- und Integralrechnung (HDI) verwendet. Seine Formel lautet allgemein:

Berechnung eines bestimmten Integrals

$\int\limits_{\textcolor{orange}{a}}^{\textcolor{red}{b}} f(x) dx = \biggl[F(x)\biggr]\limits_{\textcolor{orange}{a}}^{\textcolor{red}{b}} = F({\textcolor{red}{b}}) - F({\textcolor{orange}{a}}).$

Bestimmtes Integral berechnen Beispiel

Schau dir gleich noch ein Beispiel an, um das bestimmte Integral zu üben:

$\int \limits_{-\pi}^\pi \sin(x) \, dx$

Schritt 1: Bestimme die Stammfunktion F(x)

$F(x) = -\cos(x)$

Schritt 2: Schreibe F(x) in eckige Klammern und dahinter die Integrationsgrenzen.

$\[\int \limits_{\textcolor{orange}{-\pi}}^{\textcolor{red}{\pi}} \sin(x) \, dx = \biggl[-\cos(x) \biggr]\limits_{\textcolor{orange}{-\pi}}^{\textcolor{red}{\pi}}$

Schritt 3: Berechne des bestimmte Integral. Rechne dazu:

$\int \limits_{\textcolor{orange}{-\pi}}^{\textcolor{red}{\pi}} \sin(x) \, dx = \biggl[-\cos(x) \biggr]\limits_{\textcolor{orange}{-\pi}}^{\textcolor{red}{\pi}} = -\cos({\textcolor{red}{\pi}}) - (- \cos({\textcolor{orange}{-\pi}})) = 1-1 = 0$

Hier siehst du den dazugehörigen Graphen:

Sinus Flächeninhalt Integral — Beispiel 2: Bestimmtes Integral der Sinus-Funktion

Vielleicht fragst du dich, warum die Fläche hier nicht 0 groß ist. Das liegt daran, dass ein Teil der blauen Fläche unterhalb der x-Achse liegt und deshalb negativ gezählt werden muss. Wie das genau funktioniert, erfährst du im nächsten Abschnitt!

Bestimmtes Integral berechnen – Besonderheiten

Um bestimmte Integrale auszurechnen, gibt es einige Tricks und Regeln, die dir das Leben leichter machen. Hier haben wir sie zusammengefasst:

„positiver“ und „negativer“ Flächeninhalt

Wie du im Beispiel gesehen hast, kannst du den Flächeninhalt zwischen Funktion und x-Achse nicht so leicht berechnen, wenn die Funktion zwischen den Integrationsgrenzen oberhalb und unterhalb der x-Achse verläuft.

In diesem Fall musst du das Integral aufteilen und separat von einer Nullstelle bis zur nächsten integrieren . Die Beträge davon addierst du dann.

Den Flächeninhalt des Beispiels berechnest du wie folgt:

$A = \left| \int \limits_{-\pi}^0\sin(x)dx\right| +\left| \int \limits_0^\pi \sin(x)dx\right|$

$=\left| \biggl[-\cos(x)\biggr]\limits_{-\pi}^0\right| + \left| \biggl[-\cos(x)\biggr]\limits_0^\pi\right|$

$= \left|-\cos(0)+\cos(-\pi)\right| + \left|-\cos(\pi)+\cos(0)\right| = 2+2 = 4$

Umgekehrte Summenregel

Willst du ein unbestimmtes Integral berechnen, kannst du dazu die Summenregel verwenden. Bei bestimmten Integralen bietet es sich oft an, die Aussage umgekehrt anzuwenden, d.h. Integrale mit denselben Integrationsgrenzen zusammenzufassen.

$\int\limits_a^b f(x) dx + \int\limits_a^b g(x) dx = \int\limits_a^b f(x) + g(x) dx$

Zusammenfassen von Integrationsgrenzen

Ganz ähnlich ist die folgende Regel

$\int\limits_a^b f(x) dx + \int\limits_b^c f(x) dx= \int\limits_a^c f(x) dx$

Gleiche Integrationsgrenzen

Für alle $a \in \mathbb{R}$ ist

$\int\limits_a^a f(x) dx = 0.$

Das ist anschaulich klar, wenn du den Flächeninhalt bedenkst.

Vertauschte Integrationsgrenzen

Du kannst bei einem bestimmten Integral die Integrationsgrenzen vertauschen. Dann gilt

$\int\limits_a^b f(x) dx = - \int\limits_b^a f(x) dx$

Jetzt weißt du alles Wichtige über bestimmte Integrale und kannst sie berechnen. Nun wollen wir dir noch erklären, was ein unbestimmtes Integral ist.

Unbestimmtes Integral

Ein unbestimmtes Integral hat keine Integrationsgrenzen. Du berechnest es mithilfe der Stammfunktion. Weil du zu jeder Funktion unendlich viele Stammfunktionen finden kannst, gibt das unbestimmte Integral die Menge aller Stammfunktionen an.

Unbestimmte Integrale sehen allgemein so aus:

$\int f(x) \, dx$

Beispielweise kann f(x) = 2x sein:

$\int \textcolor{teal}{2x} \, dx$

Achtung! — Die Konstante

Jede Funktion, die abgeleitet f(x) ergibt, bezeichnest du als Stammfunktion. Bei f(x) = 2x ist das zum Beispiel x², aber auch x² + 1 oder x² + 3. Das ist so, weil die Zahl am Ende beim Ableiten sowieso wegfällt. Jede Stammfunktion hat deshalb allgemein die Form

F(x) = x² + C

C ist dabei eine beliebige Zahl.

Deshalb kannst du für unbestimmte Integrale auch schreiben:

$\int f(x) \, dx = \textcolor{red}{F(x)} + \textcolor{blue}{C}$

Unbestimmtes Integral berechnen Beispiele