Differentialquotient
Du willst wissen, was der Differentialquotient genau ist und wo der Unterschied zum Differenzenquotient liegt? Hier und im Video erklären wir dir alles, was du dazu wissen musst.
Inhaltsübersicht
Differenzenquotient und Differentialquotient
Der Differentialquotient (auch Differenzialquotient) gibt die lokale Änderungsrate einer Funktion an einer betrachteten Stelle an. Der Differenzenquotient hingegen gibt die mittlere Änderungsrate der Funktion über ein betrachtetes Intervall an.
Für viele Anwendungen innerhalb der Mathematik und in der Praxis ist es wichtig, das Änderungsverhalten einer Funktion zu beschreiben. Im Folgenden soll dabei immer von einer reellwertigen Funktion einer Variablen die Rede sein.

Um das Änderungsverhalten der Funktion um eine betrachtete Stelle zu beschreiben, wird die Differenz des Funktionswertes an dieser Stelle und des Werts an einer variablen Stelle untersucht:

Diese Differenz wird allerdings erst dann wirklich aussagekräftig, wenn in Betracht gezogen wird, wie groß der Abstand zwischen den beiden betrachteten Stellen ist. Dadurch ergibt sich der Differenzenquotient im Intervall ![Rendered by QuickLaTeX.com \left[x_0;x\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-54ec67cd974b5450d3ddf5fcc059c68f_l3.png) :
:
 Differenzenquotient
Differenzenquotient
Mittlere Änderungsrate und Sekantensteigung
Der Differenzenquotient lässt sich als mittlere Änderungsrate der Funktion  auf dem Intervall
auf dem Intervall ![Rendered by QuickLaTeX.com \left[x_0;x\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-54ec67cd974b5450d3ddf5fcc059c68f_l3.png) interpretieren. Beschreibt die Funktion beispielsweise eine zurückgelegte Wegstrecke
interpretieren. Beschreibt die Funktion beispielsweise eine zurückgelegte Wegstrecke  in Abhängigkeit der Zeit
in Abhängigkeit der Zeit  , so stellt der Differenzenquotient die Durchschnittsgeschwindigkeit zwischen den Zeitpunkten
, so stellt der Differenzenquotient die Durchschnittsgeschwindigkeit zwischen den Zeitpunkten  und
und  dar.
dar.
Der Differenzenquotient kann allerdings auch geometrisch interpretiert werden. Wird durch die beiden Punkte  und
und  auf dem Graphen von
auf dem Graphen von  eine Gerade gelegt, so entspricht der Differenzenquotient der Steigung dieser Geraden. Da die Gerade eine Sekante durch den Funktionsgraphen darstellt, kann der Differenzenquotient also auch als Sekantensteigung interpretiert werden.
eine Gerade gelegt, so entspricht der Differenzenquotient der Steigung dieser Geraden. Da die Gerade eine Sekante durch den Funktionsgraphen darstellt, kann der Differenzenquotient also auch als Sekantensteigung interpretiert werden.
In den meisten Fällen ist allerdings nicht das Änderungsverhalten der Funktion auf einem Intervall von Interesse, sondern vielmehr das lokale Änderungsverhalten an der Stelle  . Aus dem Differenzenquotienten ergibt sich dies durch Annäherung der Stelle
. Aus dem Differenzenquotienten ergibt sich dies durch Annäherung der Stelle  an die Stelle
an die Stelle  und der damit verbundenen Verkleinerung des betrachteten Intervalls.
und der damit verbundenen Verkleinerung des betrachteten Intervalls.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lokale Änderungsrate und Tangentensteigung
Der Differentialquotient  an der Stelle
an der Stelle  ist der Grenzwert des Differenzenquotienten für
ist der Grenzwert des Differenzenquotienten für  :
:
 Differentialquotient
Differentialquotient
Er wird auch als Ableitung bezeichnet und beschreibt also die lokale Änderungsrate (bzw. momentane Änderungsrate) der Funktion an der Stelle  . Für eine Funktion, die eine zurückgelegte Wegstrecke
. Für eine Funktion, die eine zurückgelegte Wegstrecke  in Abhängigkeit der Zeit
in Abhängigkeit der Zeit  beschreibt, gibt der Differentialquotient die Momentangeschwindigkeit zum Zeitpunkt
beschreibt, gibt der Differentialquotient die Momentangeschwindigkeit zum Zeitpunkt  an. Dies geht einher mit der Vorstellung des Grenzübergangs des Differenzenquotienten. Der Differenzenquotient gibt nämlich die Durchschnittsgeschwindigkeit auf dem betrachteten Intervall an und der Grenzübergang bedeutet nichts anderes als dass dieses Intervall immer weiter verkleinert wird.
an. Dies geht einher mit der Vorstellung des Grenzübergangs des Differenzenquotienten. Der Differenzenquotient gibt nämlich die Durchschnittsgeschwindigkeit auf dem betrachteten Intervall an und der Grenzübergang bedeutet nichts anderes als dass dieses Intervall immer weiter verkleinert wird.
Ebenso lässt sich der Grenzübergang grafisch veranschaulichen. Dabei wandert der Punkt  auf dem Funktionsgraphen immer weiter in Richtung des Punktes
auf dem Funktionsgraphen immer weiter in Richtung des Punktes  und schließlich gleicht die Sekante durch diese beiden Punkte immer mehr der Tangente am Punkt
und schließlich gleicht die Sekante durch diese beiden Punkte immer mehr der Tangente am Punkt  .
.
Der Differentialquotient  an der Stelle
an der Stelle  gibt die Tangentensteigung an dieser Stelle an.
gibt die Tangentensteigung an dieser Stelle an.
| Bezeichnung | Formel | Bedeutung | Geometrische Bedeutung |
| Differenzenquotient |  |
mittlere
Änderungsrate |
Sekantensteigung |
| Differentialquotient |  |
lokale bzw. momentane
Änderungsrate |
Tangentensteigung |
Differentialquotient: Definition und Differenzierbarkeit
Eng in Verbindung mit dem Differentialquotienten steht der Begriff der Differenzierbarkeit.
Sei  ein offenes Intervall und
ein offenes Intervall und  eine Funktion. Diese Funktion
eine Funktion. Diese Funktion  heißt an der Stelle
heißt an der Stelle  differenzierbar, falls der Grenzwert
differenzierbar, falls der Grenzwert

existiert. Dieser Grenzwert entspricht ja gerade dem Differentialquotienten von  an der Stelle
an der Stelle  und wird wie bereits erwähnt auch als Ableitung von
und wird wie bereits erwähnt auch als Ableitung von  an der Stelle
an der Stelle  bezeichnet. Sei
bezeichnet. Sei  auf der Menge
auf der Menge  differenzierbar, so heißt die Funktion
differenzierbar, so heißt die Funktion


Ableitungsfunktion von  .
.
Für diese Funktion 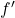 lässt sich nun wieder der Differentialquotient bestimmen. Diesen nennt man dann die zweite Ableitung von
lässt sich nun wieder der Differentialquotient bestimmen. Diesen nennt man dann die zweite Ableitung von  und sie wird häufig mit
und sie wird häufig mit  abgekürzt.
abgekürzt.
h-Methode
Für die explizite Berechnung der Ableitung ist die eben eingeführte Formulierung des Differentialquotienten meistens unvorteilhaft.
Wird allerdings in der Formulierung  des Differentialquotienten
des Differentialquotienten  durch
durch  ersetzt, so wird der Grenzübergang
ersetzt, so wird der Grenzübergang  zu
zu  und es ergibt sich folgende Formulierung des Differentialquotienten:
und es ergibt sich folgende Formulierung des Differentialquotienten:

Auf diese Weise ist die explizite Berechnung meistens deutlich einfacher als mit der ursprünglichen Formulierung. Man spricht dabei von der h-Methode.
Differentialquotient Beispiel: Ableitung der wichtigsten Funktionen
Im Folgenden soll, anhand einiger Beispielaufgaben zum Differentialquotienten, die explizite Berechnung des Differentialquotienten mit der h-Methode demonstriert werden.
Quadratische Funktion
Zunächst soll die quadratische Funktion betrachtet werden, für welche der Differentialquotient noch recht einfach zu berechnen ist.

Zunächst wird die Funktion in die Definition des Differentialquotienten eingesetzt:

Dieser Ausdruck lässt sich durch elementare Umformungen vereinfachen:
![Rendered by QuickLaTeX.com f^\prime\left(x_0\right)=\lim\limits_{h\rightarrow0}{\frac{x_0^2+2x_0h+h^2-x_0^2}{h}}=\lim\limits_{h\rightarrow0}{\frac{2x_0h+h^2}{h}=\lim\limits_{h\rightarrow0}{\left[2x_0+h\right]}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-be01129fc7232cd9bafea2cd6bf9b3a6_l3.png)
Dieser Grenzwert ist leicht zu bestimmen und es ergibt sich für den Differentialquotienten der quadratischen Funktion  der folgende Ausdruck:
der folgende Ausdruck:
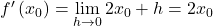
Potenzfunktion
Nun soll der Differentialquotient einer allgemeinen Potenzfunktion

berechnet werden. Hierbei soll  eine beliebige natürliche Zahl sein. Es gilt:
eine beliebige natürliche Zahl sein. Es gilt:

Mithilfe des binomischen Lehrsatzes lässt sich dieser Ausdruck vereinfachen:

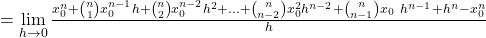
![Rendered by QuickLaTeX.com =\lim \limits_{h \rightarrow 0} \left[\binom{n}{1}x_0^{n-1} + \binom{n}{2}x_0^{n-2}h + ... + \binom{n}{n-2}x_0^2 h^{n-3} + \binom{n}{n-1}x_0h^{n-2} + h^{n-1} \right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9ab3829a6c926baea05ec72567f1baf1_l3.png)
Auch dieser Grenzwert lässt sich leicht bestimmen und für die Ableitung der Funktion  an der Stelle
an der Stelle  gilt:
gilt:

Wurzel Funktion
Hier soll die Ableitung der Wurzel-Funktion

bestimmt werden. Einsetzen in die Definition ergibt:

Der Bruch wird nun geschickt erweitert:

Anschließend wird der Ausdruck vereinfacht:

Letztlich lässt sich der Grenzwert wieder recht einfach bestimmen und es gilt für die Ableitung der Wurzelfunktion  an der Stelle
an der Stelle  :
:

Funktion 1/x
Letztendlich soll noch die Ableitung der Funktion

mittels der h-Methode bestimmt werden. Es gilt:

Zunächst werden die beiden Brüche im Zähler auf einen gemeinsamen Nenner gebracht:

Dann wird der Ausdruck vereinfacht:

Letztendlich kann der Grenzwert bestimmt werden und die Ableitung der Funktion  an der Stelle
an der Stelle  lautet demnach:
lautet demnach:

Differentialquotient und Ableitungsregeln
Mithilfe der h-Methode lassen sich Regeln finden, wie verschiedene Verknüpfungen zweier Funktionen allgemein abgeleitet werden können. Mit Hilfe dieser Regeln kann dann die Ableitung einer Funktion auf bereits bekannte Fälle zurückgeführt werden und es muss nicht jedes Mal mühsam der Differentialquotient berechnet werden.
Im Folgenden sollen Funktionen  , die in
, die in  differenzierbar sind, betrachtet werden.
differenzierbar sind, betrachtet werden.
Faktorregel
Für  ist auch die Funktion
ist auch die Funktion  in
in  differenzierbar und es gilt:
differenzierbar und es gilt:

Beweis:

Summenregel
Die Funktion  ist in
ist in  differenzierbar und es gilt:
differenzierbar und es gilt:

Beweis:


Produktregel
Auch die Funktion  ist in
ist in  differenzierbar und es gilt:
differenzierbar und es gilt:

Beweis:





Quotientenregel
Ist  für alle
für alle  , dann ist auch die Funktion
, dann ist auch die Funktion  in
in  differenzierbar und es gilt:
differenzierbar und es gilt:
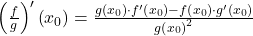
Beweis:
Zunächst soll der Spezialfall  betrachtet werden. Der allgemeine Fall folgt dann aus der Produktregel.
betrachtet werden. Der allgemeine Fall folgt dann aus der Produktregel.


Mit der Produktregel gilt nun:

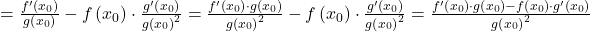
Differentialquotient — häufigste Fragen
(ausklappen)
Differentialquotient — häufigste Fragen
(ausklappen)-
Wann gibt es an einer Stelle keinen Differentialquotienten, obwohl der Graph dort weitergeht?Einen Differentialquotienten gibt es dort nicht, wo die Tangentensteigung nicht eindeutig ist. Das passiert bei Ecken und Knicken (links und rechts unterschiedliche Steigung), bei Spitzen wie bei
 in 0 oder bei senkrechten Tangenten, wenn die Steigung gegen unendlich geht.
in 0 oder bei senkrechten Tangenten, wenn die Steigung gegen unendlich geht.
-
Welche typischen Rechenfehler passieren bei der h-Methode, wenn ich den Grenzwert h → 0 bilde?Typisch sind Fehler beim Kürzen, weil h zu früh durch 0 ersetzt wird. Außerdem werden Klammern beim Ausmultiplizieren von
 vergessen oder Vorzeichen vertauscht, sodass sich Terme nicht korrekt aufheben. Häufig bleibt auch ein h im Nenner stehen, wodurch fälschlich eine Division durch 0 entsteht.
vergessen oder Vorzeichen vertauscht, sodass sich Terme nicht korrekt aufheben. Häufig bleibt auch ein h im Nenner stehen, wodurch fälschlich eine Division durch 0 entsteht.
-
Wie erkenne ich im Graphen den Unterschied zwischen einer Sekante und einer Tangente, wenn die Punkte sehr nah beieinander liegen?Eine Sekante schneidet den Graphen in zwei Punkten, eine Tangente berührt ihn in genau einem Punkt. Wenn die Punkte sehr nah sind, verlängere die Gerade gedanklich: Die Sekante trifft den Graphen (meist) nochmals, die Tangente passt nur lokal und weicht dann ab.
-
Warum reicht es nicht, einfach h = 0 in den Differenzenquotienten einzusetzen?Nein, das geht nicht, weil dann im Nenner 0 steht und der Quotient nicht definiert ist. Der Differentialquotient entsteht erst als Grenzwert, wenn h gegen 0 geht und sich zuvor ein Faktor h wegkürzen lässt. Beispiel: Bei
 wird aus
wird aus  erst nach dem Kürzen
erst nach dem Kürzen  .
.
-
Wie unterscheide ich Ableitung an einer Stelle f′(x₀) von der Ableitungsfunktion f′(x)?f′(x₀) ist eine Zahl, nämlich die Tangentensteigung genau bei
 . f′(x) ist dagegen eine neue Funktion, die jedem x die passende Steigung zuordnet. Beispiel: Für
. f′(x) ist dagegen eine neue Funktion, die jedem x die passende Steigung zuordnet. Beispiel: Für  gilt
gilt  , und bei
, und bei  ist
ist  .
.
Differenzenquotient
Klasse! Jetzt kennst du dich mit dem Differentialquotienten aus. Auch den Differenzenquotienten hast du in diesem Artikel schon kennengelernt. Willst du mehr über ihn erfahren? Dann schau direkt in unser Video .

