Integration durch Substitution
Bei der Integration durch Substitution muss man einige Punkte beachten. In diesem Zusammenhäng erklären wir zunächst die Integrationsformel und beweisen deren Gültigkeit. Anschließend zeigen wir anhand einiger Beispiele, wie du damit Integrationsaufgaben in der Praxis lösen kannst.
Kurz und kompakt haben wir für dich das Thema auch in einem Video aufbereitet. Dort werden die Zusammenhänge gut einprägsam veranschaulicht, was dir das Lernen erleichtern dürfte.
Inhaltsübersicht
Integration durch Substitution einfach erklärt
Das Ziel der Substitution ist es, ein kompliziertes Integral in ein einfacheres zu überführen. Bei der Integration durch Substitution wird in der Praxis meist die Integrationsvariable  so durch eine Funktion
so durch eine Funktion  ersetzt, also substituiert, sodass sich der Integrand vereinfacht.
ersetzt, also substituiert, sodass sich der Integrand vereinfacht.
Substitutionsregel
Dabei gilt die folgende Gleichung für eine stetige Funktion  und eine stetig differenzierbare Funktion
und eine stetig differenzierbare Funktion  :
:
 .
.
Deren Gültigkeit lässt sich mit dem Hauptsatz der Differential- und Integralrechnung beweisen. Sei  eine Stammfunktion von
eine Stammfunktion von  , dann gilt mit der Kettenregel
, dann gilt mit der Kettenregel  und weiter:
und weiter:
 .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Substitution und Differentiale
Bei der praktischen Anwendung der Substitutionsregel ersetzt man meist die Variable  durch die Funktion
durch die Funktion  :
:
 .
.
Wenn man diesen Ausdruck nun nach  ableitet und anschließend die Gleichung umstellt, erhält man:
ableitet und anschließend die Gleichung umstellt, erhält man:
 ,
,
 .
.
Setzt man nun  und
und  in die rechte Seite der Substitutionsregel ein, wird plausibel, dass die Regel stimmt.
in die rechte Seite der Substitutionsregel ein, wird plausibel, dass die Regel stimmt.
Daraus ergibt sich auch schon eine Anleitung für ein Verfahren der Substitution. Es muss lediglich die Funktion  noch so bestimmt werden, dass der Integrand auf der linken Seite der Gleichung gegenüber dem Integranden auf der rechten Seite vereinfacht wird. Das gelingt meistens, wenn eine verschachtelte Funktion im Integranden vorliegt.
noch so bestimmt werden, dass der Integrand auf der linken Seite der Gleichung gegenüber dem Integranden auf der rechten Seite vereinfacht wird. Das gelingt meistens, wenn eine verschachtelte Funktion im Integranden vorliegt.
Integration durch Substitution Beispiel
Wir betrachten zum Beispiel die Funktion
 .
.
Dann könnte man die Funktion zu der Funktion  vereinfachen wollen. Es müsste also gelten:
vereinfachen wollen. Es müsste also gelten:
 .
.
Diesen Ausdruck kann man nun nach  umstellen und nennt den erhaltenten Term
umstellen und nennt den erhaltenten Term  :
:
 .
.
Jetzt gilt nämlich  , was genau das Ziel war. Nun muss nur noch die Funktion
, was genau das Ziel war. Nun muss nur noch die Funktion  abgeleitet werden und man hätte die Substitutionsgleichung einmal von rechts nach links angewandt:
abgeleitet werden und man hätte die Substitutionsgleichung einmal von rechts nach links angewandt:
 .
.
Allerdings lässt sich diese Methode noch verkürzen. Man muss die Funktion  gar nicht explizit bestimmen. Man kann einfach die Gleichung
gar nicht explizit bestimmen. Man kann einfach die Gleichung  in der Funktion
in der Funktion  einsetzen und erhält automatisch
einsetzen und erhält automatisch  . Ebenso kann man einfach den Ausdruck
. Ebenso kann man einfach den Ausdruck  nach
nach  ableiten und nach
ableiten und nach  umstellen.
umstellen.


Diesen Ausdruck kann man nun ebenso wie  im Integral einsetzen:
im Integral einsetzen:
 .
.
Integration durch Substitution Grenzen
Bei dem eben gezeigten Beispiel haben wir die Integrationsgrenzen noch nicht beachtet. Wir müssen aus 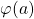 und
und  noch die Grenzen
noch die Grenzen  und
und  berechnen. Dazu benötigen wir also die Umkehrfunktion von
berechnen. Dazu benötigen wir also die Umkehrfunktion von  . Diese kennen wir aber schon. Wir haben nämlich
. Diese kennen wir aber schon. Wir haben nämlich  bestimmt, indem wir
bestimmt, indem wir  nach x umgestellt haben. Um die Umkehrfunktion zu erhalten müssen wir also wieder nach
nach x umgestellt haben. Um die Umkehrfunktion zu erhalten müssen wir also wieder nach  umstellen und erhalten somit
umstellen und erhalten somit  . In diese Funktion müssen wir also noch die ursprünglichen Integrationsgrenzen einsetzen, um die neuen Grenzen zu erhalten. Lauten in unserem Beispiel die Grenzen also 2 und 7, so wären die neuen Grenzen 4 und 14:
. In diese Funktion müssen wir also noch die ursprünglichen Integrationsgrenzen einsetzen, um die neuen Grenzen zu erhalten. Lauten in unserem Beispiel die Grenzen also 2 und 7, so wären die neuen Grenzen 4 und 14:
 .
.
Es wäre bei der eben beschriebenen Methode auch möglich die Integrationsgrenzen zunächst nicht zu beachten und eine Stammfunktion zu finden, bevor man  wieder rücksubstituiert. Abschließend kann die Stammfunktion an den ursprünglichen Grenzen ausgewertet werden.
wieder rücksubstituiert. Abschließend kann die Stammfunktion an den ursprünglichen Grenzen ausgewertet werden.
Integration durch Substitution Aufgaben
Bei der eben beschriebenen Methode der Integration durch Substitution rechnet man die Substitutionsgleichung im Grunde von rechts nach links durch. Diese Methode wollen wir nun an einer Beispielaufgabe noch einmal demonstrieren. Allerdings wollen wir auch zeigen, wie man die Aufgabe mittels der Substitutionsgleichung von links nach rechts lösen kann, indem man die Struktur des Integranden genauer betrachtet. Diese zweite Methode demonstrieren wir dann nochmal in einem extra Beispiel.
Integration durch Substitution Beispiel 1
Wir betrachten zunächst folgendes Integral:
 .
.
Hier wollen wir die Funktion 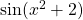 im Integranden zu
im Integranden zu  vereinfachen. Wir setzen also
vereinfachen. Wir setzen also
 .
.
Nun können wir das nach  ableiten und anschließend nach
ableiten und anschließend nach  umstellen:
umstellen:
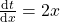 ,
,
 .
.
Setzen wir nun  und
und  in das Integral ein und passen unsere Integrationsgrenzen an, so erhalten wir:
in das Integral ein und passen unsere Integrationsgrenzen an, so erhalten wir:

![Rendered by QuickLaTeX.com =\int\limits_{2}^{27}\frac{1}{2} \sin(t)\mathrm{d}t=\left[-\frac{1}{2}\cos(t)\right]_{2}^{27}=-\frac{1}{2}\cos(27)+\frac{1}{2}\cos(2)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ada54622cda9055e1ffcaeed0b8832af_l3.png) .
.
Statt die Grenzen zu beachten hätte man auch folgendermaßen rechnen können:
 .
.
Zuletzt muss man dann allerdings für  wieder
wieder  einsetzen und kann dann die ursprünglichen Grenzen einsetzen:
einsetzen und kann dann die ursprünglichen Grenzen einsetzen:
![Rendered by QuickLaTeX.com \int\limits_{0}^{5} x\cdot \sin(x^2+2)\mathrm{d}x=\left[-\frac{1}{2}\cos(x^2+2)\right]_{0}^{5}=-\frac{1}{2}\cos(27)+\frac{1}{2}\cos(2)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-aa7ef15cc3bfee4836f7d5d7ed39c085_l3.png) .
.
Nun wollen wir dir noch zeigen, wie man dieses Integral lösen kann, indem man die Substitutionsgleichung von links nach rechts anwendet. Wenn man sich die linke Seite der Gleichung genauer betrachtet, erkennt man, dass der Integrand aus einer verschachtelten Funktion besteht, an die noch die Ableitung der inneren Funktion multipliziert wird. Wenn man also einen Integranden vorfindet, der genau diese Struktur aufweist, lässt sich die Gleichung ganz einfach anwenden. Und genau das ist in diesem Beispiel der Fall. Unser Integrand lautet folgendermaßen:
 .
.
Wenn wir die Funktion  als äußere Funktion betrachten, muss die innere Funktion
als äußere Funktion betrachten, muss die innere Funktion  lauten. Ihre Ableitung lautet
lauten. Ihre Ableitung lautet  . Insgesamt haben wir also
. Insgesamt haben wir also  . Das entspricht fast dem Integranden unseres Integrals, lediglich noch mit dem Faktor 2 multipliziert. Aber diesen Faktor können wir eliminieren, indem wir mit
. Das entspricht fast dem Integranden unseres Integrals, lediglich noch mit dem Faktor 2 multipliziert. Aber diesen Faktor können wir eliminieren, indem wir mit  multiplizieren. Es gilt also:
multiplizieren. Es gilt also:

Wenn wir nun unsere Variable  in
in  umbenennen, erhalten wir genau die linke Seite der Substitutionsgleichung und können sie mit der rechten Seite gleichsetzen:
umbenennen, erhalten wir genau die linke Seite der Substitutionsgleichung und können sie mit der rechten Seite gleichsetzen:
 .
.
Setzen wir nun  und
und  ein, erhalten wir das vereinfachte Integral:
ein, erhalten wir das vereinfachte Integral:
 .
.
Integration durch Substitution Beispiel 2
Im zweiten Beispiel wollen wir das folgende Integral betrachten:
 .
.
Hier erkennt man, dass der Integrand aus der äußeren Funktion  mit der inneren Funktion
mit der inneren Funktion  besteht, welche mit der Ableitung
besteht, welche mit der Ableitung  der inneren Funktion multipliziert wird. Der Integrand weißt also genau die Struktur der linken Seite der Substitutionsgleichung auf:
der inneren Funktion multipliziert wird. Der Integrand weißt also genau die Struktur der linken Seite der Substitutionsgleichung auf:
 .
.
Mithilfe der Substitutionsregel erhalten wir also folgende Lösung:

![Rendered by QuickLaTeX.com =\left[2\sqrt x\right]_2^{29}=2(\sqrt{29}-\sqrt 2)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a9e09cac725c9c3f8e7ed82f5f7aab73_l3.png) .
.
Bei dieser Methode der Integration durch Substitution wird im Grunde die Kettenregel der Differentialrechnung rückgängig gemacht.
Spezialfälle
Im folgenden sollen kurz zwei wichtige Arten von Integralen genannt werden, die sich allgemein mittels Integration durch Substitution lösen lassen.
Integration durch lineare Substitution
Besteht der Integrand aus einer verketteten Funktion, wobei die äußere Funktion  die Stammfunktion
die Stammfunktion  besitzt und die innere Funktion linear von der Form
besitzt und die innere Funktion linear von der Form  ist, so lautet die Lösung des Integrals folgendermaßen:
ist, so lautet die Lösung des Integrals folgendermaßen:
![Rendered by QuickLaTeX.com \int\limits_a^b f(ax+b)\mathrm{d}x=\left[\frac{1}{a}F(ax+b)\right]_a^b](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dd5cab65d0c7a8aa5047cf69f9592b6a_l3.png) .
.
Logarithmische Integration
Ist der Integrand ein Bruch mit einer Funktion  im Nenner und deren Ableitung
im Nenner und deren Ableitung  im Zähler, so ist der natürliche Logarithmus der Funktion
im Zähler, so ist der natürliche Logarithmus der Funktion  die gesuchte Stammfunktion.
die gesuchte Stammfunktion.
![Rendered by QuickLaTeX.com \int\limits_a^b \frac{f'(x)}{f(x)}\mathrm{d}x=\left[\ln{|f(x)|}\right]_a^b](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1468a3f276070323090b9227836cd5a2_l3.png) .
.