l‘Hospital

Hier erklären wir dir die Regel von l’Hospital zur Bestimmung des Grenzwerts einer Funktion ganz einfach und mit vielen Beispielen. Alle Fälle, bei denen du l’Hospital anwenden kannst, fassen wir übersichtlich in einer Tabelle zusammen. 

Du möchtest die Regeln von l’Hospital schnell anwenden können? Dann schau dir unser Video dazu an!

l’Hospital einfach erklärt

Mit der Regel von l’Hospital (manchmal auch hospitalsche Regel,  Satz von L’Hospital, oder nur L’Hôpital) kannst du ganz einfach den Grenzwert einer Funktion  berechnen, wenn der Limes der Funktion

 

einen unbestimmten Ausdruck  liefert. Also immer dann, wenn     oder     ist.

Dazu reicht es, wenn du dir die Ableitungen von und anschaust. Es gilt:

Was musst du also machen?

• Schritt 1: Leite beide Funktionen und 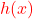unabhängig voneinander ab.
• Schritt 2: Bestimme den Grenzwert

Es kann passieren, dass du alles wie hier beschrieben berechnet hast, aber das Ergebnis immer noch unbestimmt ist, also zum Beispiel     oder . Ist das der Fall, so musst du die Regel von l’Hospital einfach noch einmal anwenden.

l’Hospital Anwendungen

Zum Glück kann man l’Hospital nicht nur verwenden, wenn    mit    oder   . Mit ein paar kleinen Tricks, kannst du die Aussage auch auf andere Funktionen übertragen. Dazu musst du sie nur auf die Form eines Quotienten  bringen. In der Tabelle zeigen wir dir alle Fälle, bei denen du mit l’Hospital Konvergenz oder Divergenz zeigen kannst und wie du die Funktionen am besten umformst. Die Spalte „Beispiele“ bezieht sich auf die im nächsten Abschnitt ausführlich berechneten Beispiele zu jedem der Fälle.

Grenzwert	Funktion	Umformung	Beispiel
		entfällt	1
			2
			3
			4

Achtung: Die Rückrichtung gilt im Allgemeinen nicht! Aus der Existenz des Grenzwertes kannst du nicht folgern, dass existiert! Falls du das nicht glauben solltest, ist hier ein Gegenbeispiel:

Aber: existiert nicht! Diese Funktion divergiert.

l’Hospital Beispiele

Jetzt weißt du viel über die Theorie, nun zeigen wir dir für die in der oberen Tabelle aufgeführten Fälle verschiedene Beispiele:

Beispiel 1: 

Gesucht ist hier Du hast also:

mit 

mit 

Wir können l’Hospital direkt anwenden! Dazu berechnen wir und und erhalten:

Manchmal kommt es auch vor, dass du die Regel von l’Hospital zweimal anwenden musst, um auf das Ergebnis zu kommen. Das erschwert die Sache zum Glück nicht besonders, wie dieses Beispiel zeigt. Gesucht sei

    mit        und   

Wir leiten beide Funktionen einmal ab, und erhalten und . Für gilt hier leider immer noch . Durch erneutes Ableiten können wir das Problem jedoch leicht lösen

Beispiel 2:

Etwas schwieriger ist die Berechnung von  Gegeben ist

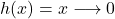für

für

Damit du l’Hospital anwenden kannst, brauchst du die zweite Transformation der Tabelle und erhältst

Ableiten liefert mit der Regel von l’Hospital den gesuchten Grenzwert. Mit und gilt:

Beispiel 3:   

Gesucht wird . Wir haben also

für

für

Um den Grenzwert mit l’Hospital zu berechnen, brauchst du die Transformation gemäß Fall 3 in der Tabelle

Zähler und Nenner leiten wir nun unabhängig voneinander ab (unter Verwendung der Produktregel )  und betrachten den Grenzwert

Beispiel 4:

Ein Beispiel für den vierten in der Tabelle aufgeführten Fall ist die Bestimmung des Grenzwertes . Hier ist und , wir haben also den Fall gegeben, denn

und

Damit wir eine Aussage zum Grenzwert treffen können, müssen wir die Funktion erst gemäß Zeile 4 der Tabelle mithilfe der e-Funktion umschreiben. Allgemein gilt , wir erhalten also

Jetzt betrachten wir nur den Limes des Exponenten mit der Regel von l’Hospital:

Damit gilt für unsere ursprüngliche Funktion