Integralrechnung
Hier fassen wir alles Wichtige zum Thema Integralrechnung zusammen und erklären es dir mit Merke-Kästen, Schritt-für Schritt-Anleitungen und Beispielen!
Statt einen langen Text zu lesen, möchtest du lieber, dass es dir jemand direkt erklärt? Schau dir dazu einfach unser Video an!
Inhaltsübersicht
Integralrechnung einfach erklärt
Die Integralrechnung ist ein Teilgebiet der Analysis, das eng mit der Differentialrechnung verknüpft ist. Genauso, wie es bei der Differentialrechnung primär um die Bestimmung der Ableitung einer Funktion geht, beschäftigt sich die Integralrechnung mit der Bestimmung einer Stammfunktion und den Aussagen, die man daraus schließen kann.
Ein Integral hat die folgende Form, die Bezeichnungen werden im Folgenden als bekannt vorausgesetzt.
In diesem Text wollen wir nacheinander alle wichtigen Kapitel zur Integralrechnung vorstellen und dir dabei die wichtigsten Infos und Rechenregeln übersichtlich und logisch erklären.
Hinweis: Eine einfachere Erklärung findest du in unserem Einsteiger-Artikel .
Stammfunktion
Die Bestimmung einer Stammfunktion ist das zentrale Thema der Integralrechnung und dient als Grundlage für alle weiteren Kapitel. Eine Stammfunktion ist wie folgt definiert:
Die Funktion  heißt Stammfunktion von
heißt Stammfunktion von  , wenn
, wenn 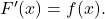
Sehr praktisch ist, dass jede stetige Funktion  eine solche Stammfunktion
eine solche Stammfunktion  besitzt. Nur wie kann man sie berechnen
?
besitzt. Nur wie kann man sie berechnen
?
Dazu verwendest du den HDI, das ist der Hauptsatz der Differential- und Integralrechnung. Er stellt den Zusammenhang zwischen Ableiten und Integrieren her.
Mit obiger Definition wäre es einfach,  zu bestimmen, wenn du die Stammfunktion
zu bestimmen, wenn du die Stammfunktion  gegeben hast. Du müsstest einfach nur ableiten. Jetzt wollen wir diesen Vorgang sozusagen rückgängig machen, du kannst Integrieren (Aufleiten) als Umkehrung vom Ableiten auffassen!
gegeben hast. Du müsstest einfach nur ableiten. Jetzt wollen wir diesen Vorgang sozusagen rückgängig machen, du kannst Integrieren (Aufleiten) als Umkehrung vom Ableiten auffassen!
Das bedeutet, du kannst eine Stammfunktion direkt über das Integral berechnen:

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel
Gesucht sei eine Stammfunktion von  . Wir suchen also eine Funktion
. Wir suchen also eine Funktion  , die abgeleitet gerade
, die abgeleitet gerade  ergibt. Dazu berechnen wir
ergibt. Dazu berechnen wir

Nun müssen wir uns überlegen, was abgeleitet 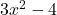 ergeben würde und sehen sofort (unter Berücksichtigung der Ableitungsregeln
), dass
ergeben würde und sehen sofort (unter Berücksichtigung der Ableitungsregeln
), dass

Merke: Die Konstante  steht für eine beliebige reelle Zahl, die beim Ableiten von
steht für eine beliebige reelle Zahl, die beim Ableiten von  weg fällt. Du siehst also sofort, dass es unendlich viele Stammfunktionen zu
weg fällt. Du siehst also sofort, dass es unendlich viele Stammfunktionen zu  gibt, je nachdem, was du für
gibt, je nachdem, was du für  einsetzt.
einsetzt.
Wie die Stammfunktionen für alle wichtigen Funktionen  aussehen und wie du sie berechnest, erklären wir dir ausführlich in einem eigenen Artikel zu den Stammfunktionen.
aussehen und wie du sie berechnest, erklären wir dir ausführlich in einem eigenen Artikel zu den Stammfunktionen.
Obige Definition der Stammfunktion ist sehr auf die Anwendung ausgelegt und zeigt dir, wie du sie am besten berechnen kannst. Etwas theoretischer kann man sie über die Integralfunktion definieren.
Integralfunktion
Als Integralfunktion wird eine Funktion bezeichnet, die die folgende Form hat:

Der Unterschied zur allgemeinen Stammfunktion besteht darin, dass hier ein bestimmtes Integral betrachtet wird, mit Untergrenze  und der Variablen
und der Variablen  als Obergrenze. Hier berechnest du also eine konkrete Stammfunktion, die im Punkt
als Obergrenze. Hier berechnest du also eine konkrete Stammfunktion, die im Punkt  eine Nullstelle hat.
eine Nullstelle hat.
Merke: Jede Integralfunktion  hat an ihrer unteren Integrationsgrenze
hat an ihrer unteren Integrationsgrenze  eine Nullstelle, d.h.
eine Nullstelle, d.h.  .
.
Merke: Jede Integralfunktion ist eine Stammfunktion, aber nicht jede Stammfunktion ist auch eine Integralfunktion. Das gilt gerade weil eine Stammfunktion beliebig nach oben/unten verschoben werden kann.
Bestimmtes Integral und unbestimmtes Integral
Wie du gerade beim Unterschied zwischen Integralfunktion und Stammfunktion gesehen hast, gibt es in der Integralrechnung zwei Arten von Integralen, nämlich das bestimmte und das unbestimmte Integral.
Die unbestimmten Integrale stehen für die Gesamtheit der Stammfunktionen  von
von  . Ein unbestimmtes Integral ist definiert als
. Ein unbestimmtes Integral ist definiert als

Unbestimmte Integrale zu bestimmen, ist eine wesentliche Aufgabe in der Integralrechnung. Dazu integrierst du  und berechnest so die allgemeine Stammfunktion. Hier ist es sehr wichtig, dass du die Konstante
und berechnest so die allgemeine Stammfunktion. Hier ist es sehr wichtig, dass du die Konstante  nicht vergisst.
nicht vergisst.
Etwas schwieriger ist die Berechnung eines bestimmten Integrals. Es unterscheidet sich vom unbestimmten Integral nur durch die explizit angegebenen Integrationsgrenzen  und
und  .
.

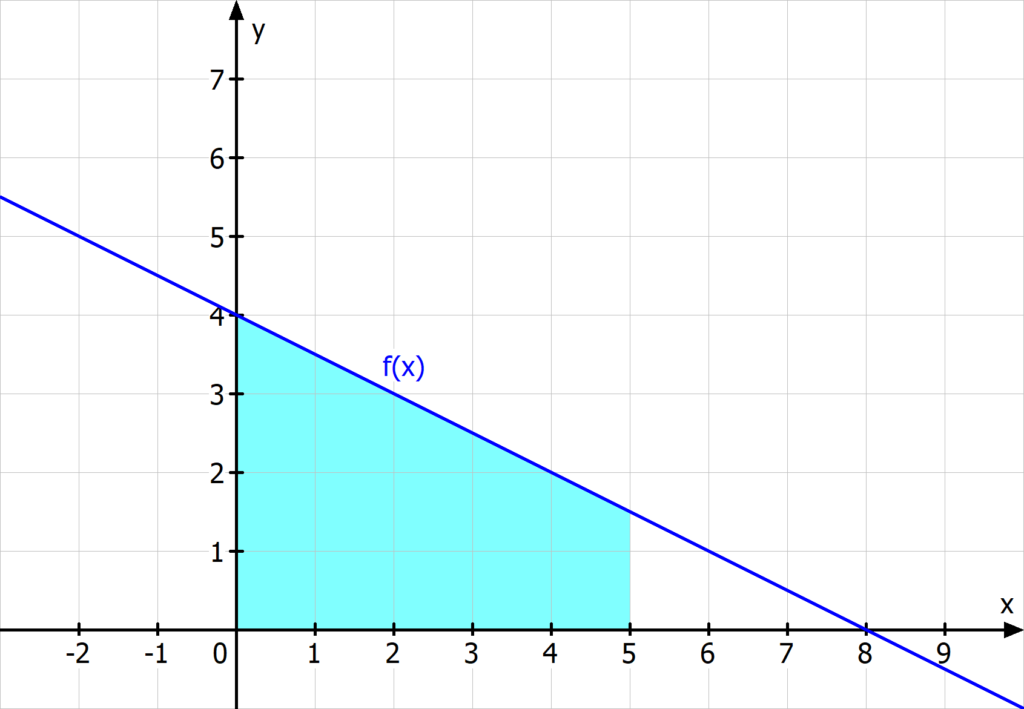
Willst du ein bestimmtes Integral berechnen, so interessierst du dich für die (mit einem Vorzeichen skalierte) Fläche, die  im Intervall
im Intervall ![Rendered by QuickLaTeX.com \left[a,b\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f7cb615e2122119417a7baa11c68fdc0_l3.png) mit der x-Achse einschließt. Als Ergebnis erhältst du keine Funktion, sondern eine Zahl!
mit der x-Achse einschließt. Als Ergebnis erhältst du keine Funktion, sondern eine Zahl!
![Rendered by QuickLaTeX.com \int\limits_a^b f(x) dx = \biggl[F(x)\biggr]\limits_a^b = F(b) - F(a).](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-18df88101311dba572142cc61a9dbace_l3.png)
Zur Berechnung benötigst du die obige Formel. Dabei kann gar nichts schief gehen, wenn du die folgende Schritt-für-Schritt-Anleitung befolgst.
Anleitung: Bestimmtes Integral berechnen
| Schritt 1: | Berechne die Stammfunktion F(x) von f(x) und schreibe sie in eckige Klammern. Bringe sie also auf die Form ![Rendered by QuickLaTeX.com \biggl[F(x)\biggr]\limits_a^b](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-514ef2194e43715ca0571fb49b45d48f_l3.png)
|
| Schritt 2: | Setze nun deine beiden Integrationsgrenzen a und b in die Stammfunktion ein und berechne also F(a) und F(b). |
| Schritt 3: | Ziehe F(a) von F(b) ab, d.h. berechne F(b) – F(a). |
Die genaue Vorgehensweise verstehst du am besten im nächsten Abschnitt anhand von einem kurzen Beispiel.
Beispiel zum bestimmten Integral
Wir wollen das folgende bestimmte Integral berechnen

-
Schritt 1: Wir berechnen die Stammfunktion
 und schreiben sie in eckige Klammern:
und schreiben sie in eckige Klammern:
![Rendered by QuickLaTeX.com \biggl[-\frac{1}{4}x^2+4x\biggr]\limits_0^5](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b0c6a8d464920c34bd4cd2031028530b_l3.png)
- Schritt 2: Nun setzen wir die beiden Integrationsgrenzen ein, wir berechnen also
![Rendered by QuickLaTeX.com F(5) = \biggl[ -\frac{1}{4}\cdot 5^2+4\cdot 5\biggr]= 13,75](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-96e5f22517198f328f9d6169e59bdb43_l3.png) und
und ![Rendered by QuickLaTeX.com F(0)= \biggl[-\frac{1}{4}\cdot 0^2+4\cdot 0\biggr] = 0](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5ad427c55eca5099365ed78f01253d0c_l3.png) .
.
- Schritt 3: Als letztes ziehen wir die beiden Werte voneinander ab

Mit dieser Integralrechnung weißt du, dass dein Integral mit der x-Achse im Intervall ![Rendered by QuickLaTeX.com [0,2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c6cc9e42627fb0516082896ece53b0b3_l3.png) ein Flächenstück mit dem Flächeninhalt
ein Flächenstück mit dem Flächeninhalt  einschließt.
einschließt.
Merke: Beim Integrieren eines bestimmten Integrals kannst du diese Konstante  einfach weglassen, da sie in Schritt 3 sowieso wegfallen würde.
einfach weglassen, da sie in Schritt 3 sowieso wegfallen würde.
Zur Integralrechnung mit bestimmten Integralen gibt es noch einige Besonderheiten, d.h. Regeln, die dir sagen, wann du ein Integral in einer Integralrechnung zusammenfassen darfst, oder wie du die Integrationsgrenzen vertauschst. Ausführlich findest du diese Regeln im Video zu den bestimmten und unbestimmten Integralen erklärt.
Bisher kennst du den Unterschied zwischen einem bestimmten und einem unbestimmten Integral und weißt, was eine Stammfunktion ist. Wir haben dir aber noch nicht genauer erklärt, wie du die Stammfunktion bei einer Integralrechnung findest, d.h. wie du integrierst. Im nächsten Abschnitt fassen wir die Regeln kurz zusammen, ausführlich erklärt und mit vielen weiteren Beispielen und Aufgaben findest du sie in unserem Video zu den Integrationsregeln .
Integrationsregeln
Genauso wie es beim Ableiten verschiedene Regeln, wie z.B. die Produktregel oder die Quotientenregel gibt, musst du auch beim Integrieren einiges beachten. Immerhin machst du die Ableitungsregeln sozusagen „rückgängig“. Was genau du zu tun hast, erklären wir dir in den nächsten Abschnitten. Dabei formulieren wir die Integrationsregeln nur für unbestimmte Integrale, für bestimmte Integrale gelten sie natürlich analog.
- Die wichtigste Regel der Integralrechnung ist die Potenzregel, die immer dann verwendet wird, wenn die Integralrechnung Potenzfunktionen enthält. Sie besagt
Potenzregel

Offensichtlich erhält man beim Ableiten der rechten Seite wieder  .
.
- Die Faktorregel ist die einfachste Integrationsregel. Du benutzt sie immer, wenn deine Funktion einen konstanten Faktor enthält. Diesen kannst du dann „vor das Integral ziehen“, du klammerst ihn sozusagen aus. Es gilt
Faktorregel

- Die dritte der Integrationsregeln ist die Summenregel. Du verwendest sie immer, wenn dein Integral eine Summe enthält. Mit dieser Integrationsregel kannst du das Integral aufsplitten und die beiden Summanden einzeln berechnen. Das bedeutet
Summenregel

- Wenn das Integral stattdessen eine Differenz enthält, gehst du analog zur Summenregel vor und erhältst die Differenzregel
Differenzregel

Beispiel
Um die nachfolgende Integralrechnung durchzuführen, benötigen wir alle obigen Integrationsregeln. Gesucht sei

Mithilfe der Summen- und der Differenzregel dürfen wir das Integral im ersten Schritt „auseinanderziehen“ und erhalten

Nun wenden wir jeweils die Faktorregel und die Potenzregel an, integrieren und erhalten

- Auch für Sinus und Cosinus gibt es in der Integralrechnung spezielle Regeln.
Integration von Sinus und Cosinus

-
Bei der e-Funktion ist die Integralrechnung nicht schwer:
Integration e-Funktion
Etwas komplizierter ist es bei der ln-Funktion
 . Hier kannst du das Integral mithilfe der partiellen Integration bestimmen und erhältstIntegration ln-Funktion
. Hier kannst du das Integral mithilfe der partiellen Integration bestimmen und erhältstIntegration ln-Funktion
Vielleicht weißt du, dass von
 die Ableitung
die Ableitung  ist. Damit ist
ist. Damit ist  natürlich die Stammfunktion von
natürlich die Stammfunktion von  . Dies ist ein Spezialfall der logarithmischen Integrationsregelnlogarithmische Integration
. Dies ist ein Spezialfall der logarithmischen Integrationsregelnlogarithmische Integration
Beispiel
Wir wollen die Funktion  integrieren, also
integrieren, also

Bei genauer Betrachtung des Zählers und des Nenners siehst du, dass im Zähler beinahe die Ableitung des Nenners steht. Um die logarithmische Integrationsregel anwenden zu können, musst du den Zähler also etwas umformen. Dazu klammern wir  aus und ziehen es mit der Faktorregel vor das Integral:
aus und ziehen es mit der Faktorregel vor das Integral:

Nun können wir die Regel der logarithmischen Integration anwenden und erhalten als Ergebnis 
Merke: In den meisten Fällen, in denen du die Stammfunktion eines Bruches berechnen musst, verwendest du entweder die logarithmische Integrationsregel oder schreibst den Ausdruck in eine Potenzfunktion um.
Flächenintegral
Mit einem bestimmten Integral kann das Flächenstück berechnet werden, das der Funktionsgraph mit der x-Achse im Intervall zwischen den Integrationsgrenzen einschließt. Grund hierfür ist die Definition des Integrals als Grenzwert der Ober- bzw. Untersummen einer Funktion. Was genau das zu bedeuten hat, erfährst du im nächsten Abschnitt.
Obersumme und Untersumme
Eine alternative Definition des Integrals benutzt die Obersumme und die Untersumme. Die Idee dabei ist, dass der Flächeninhalt, den eine Funktion mit der x-Achse im Intervall ![Rendered by QuickLaTeX.com [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b7e4beaceae66bed938a06185209134a_l3.png) einschließt, durch immer schmaler werdende Rechtecke angenähert werden kann. Je schmaler die Rechtecke dabei werden, desto genauer ist die Annäherung! Nähert man den Flächeninhalt von „unten“, so spricht man von Untersumme. Ein Beispiel mit sehr grober Unterteilung siehst du im unten stehenden Bild.
einschließt, durch immer schmaler werdende Rechtecke angenähert werden kann. Je schmaler die Rechtecke dabei werden, desto genauer ist die Annäherung! Nähert man den Flächeninhalt von „unten“, so spricht man von Untersumme. Ein Beispiel mit sehr grober Unterteilung siehst du im unten stehenden Bild.
Hier sieht man auch direkt, dass die Annäherung für schmalere Rechtecke zunehmend besser wird!
Wenn man sich dem Flächeninhalt von „oben“ her annähert, spricht man von der Obersumme. Das Prinzip ist dabei gleich, wie bei der Untersumme, auch hier zeigt dir die unten stehende Abbildung ein Beispiel für eine relativ grobe Unterteilung.
Das Integral kann man nun als Grenzwert interpretieren, dem sich Obersumme (O) und Untersumme (U) bei immer feiner werdender Unterteilung annähern. Wenn wir die Feinheit der Unterteilung als  definieren, gilt damit im Intervall
definieren, gilt damit im Intervall ![Rendered by QuickLaTeX.com [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b7e4beaceae66bed938a06185209134a_l3.png)

Achtung: Willst du mit einem bestimmten Integral das Flächenstück berechen, das der Funktionsgraph mit der x-Achse zwischen den Integrationsgrenzen einschließt, musst du das Vorzeichen bedenken! Es gilt:
![Rendered by QuickLaTeX.com f(x) > 0 \quad \forall x \in [a, b] \quad \Longrightarrow \quad \int \limits_a^b f(x) > 0](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9f8a61e4a91cd9ad25bf0f9196ac3634_l3.png)
![Rendered by QuickLaTeX.com f(x) < 0 \quad \forall x \in [a, b] \quad \Longrightarrow \quad \int \limits_a^b f(x) < 0](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c37cc366700c02075a4afac86102463e_l3.png)
Das bedeutet, dass wir den Flächeninhalt unterhalb der x-Achse nur mit einem negativen Vorzeichen versehen berechnen können. Daher musst du bei der Integralrechnung eines Flächenintegrals die im nächsten Abschnitt vorgestellte Anleitung beachten.
Anleitung: Flächenintegral berechnen
| Schritt 1: | Bestimme zuerst die Nullstellen von f(x). Liegt eine Nullstelle zwischen deinen Integrationsgrenzen? |
| Schritt 2: | Falls nein, berechne wie gewohnt das bestimmte Integral. Falls ja, unterteile dein Intervall in einen positiven und einen negativen Teil und berechne die Integrale separat. Addiere dann die Beträge der Ergebnisse. |
Damit du diese Vorgehensweise noch besser verstehst, und es dir direkt vorstellen kannst, wollen wir das Beispiel aus dem obigen Bild genauer untersuchen.
Beispiel zum Flächenintegral
Nun wollen wir uns das Flächenintegral aus obigem Bild genauer anschauen. Dort siehst du die Sinus-Funktion im Intervall ![Rendered by QuickLaTeX.com [ -\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5541e35f57e03fe8307622a9915e8274_l3.png) abgebildet. Wollen wir den Flächeninhalt berechnen, den
abgebildet. Wollen wir den Flächeninhalt berechnen, den  in diesem Intervall mit der x-Achse einschließt, betrachten wir also das Integral
in diesem Intervall mit der x-Achse einschließt, betrachten wir also das Integral

Hier sieht man sofort, dass  ist. Deswegen müssen wir unser Intervall aufteilen, um den Flächeninhalt zu bestimmen.
ist. Deswegen müssen wir unser Intervall aufteilen, um den Flächeninhalt zu bestimmen.

Diese Integralrechnung können wir nun durchführen, indem wir im ersten Schritt die Stammfunktion  von
von  bestimmen. Im zweiten Schritt setzen wir die Integrationsgrenzen ein und erhalten
bestimmen. Im zweiten Schritt setzen wir die Integrationsgrenzen ein und erhalten
![Rendered by QuickLaTeX.com =\left| \biggl[-\cos(x)\biggr]\limits_{-\pi}^0\right| + \left| \biggl[-\cos(x)\biggr]\limits_0^\pi\right|](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-87e95c02f77f76df155ff44a3d9d72bb_l3.png)

Flächen zwischen zwei Graphen
Im Abschnitt zuvor haben wir die Fläche zwischen dem Funktionsgraphen
und der x-Achse im Intervall [a,b] mithilfe des bestimmten Integrals berechnet. Integralrechnung kannst du auch dazu verwenden, um den Flächeninhalt zwischen zwei Graphen in einem bestimmten Intervall zu berechnen. Angenommen, du willst die Fläche berechnen, die die beiden Funktionsgraphen  und
und  einschließen. Die Idee ist, zuerst die Fläche zu berechnen, welche die obere Funktion mit der x-Achse einschließt, und davon dann die Fläche abziehen, die die untere Funktion mit der x-Achse einschließt. Das bedeutet:
einschließen. Die Idee ist, zuerst die Fläche zu berechnen, welche die obere Funktion mit der x-Achse einschließt, und davon dann die Fläche abziehen, die die untere Funktion mit der x-Achse einschließt. Das bedeutet:

Das allgemeine Vorgehen findest du in der Tabelle im nächsten Abschnitt erklärt.
Anleitung: Fläche zwischen zwei Graphen berechnen
| Schritt 1: | Berechne alle Schnittpunkte von f(x) und g(x), d.h. berechne f(x)=g(x). |
| Schritt 2: | Bestimme für die Intervalle zwischen den Schnittpunkten jeweils die obere und die untere Funktion. |
| Schritt 3: | Stelle die Integrale zwischen den Schnittpunkten auf, indem du die untere Funktion von der oberen abziehst. D.h. bestimme 
|
| Schritt 4: | Berechne die Integrale! |
Diese Vorgehensweise wollen wir nun an einem Beispiel umsetzen.
Beispiel zur Flächenberechnung zwischen zwei Graphen
Wir wollen mithilfe der Integralrechnung die Fläche bestimmen, die die beiden Funktionen  und
und  einschließen.
einschließen.
Dazu berechnen wir zuerst ihre Schnittpunkte. Das geht entweder mit dem Satz von Vieta, oder durch geschicktes Raten der ersten Nullstelle.




Im Intervall [2,3] ist  , während im Intervall [3,4]
, während im Intervall [3,4]  . Somit lassen sich nun die Teilintervalle aufstellen, mit denen wir den Flächeninhalt bestimmen können.
. Somit lassen sich nun die Teilintervalle aufstellen, mit denen wir den Flächeninhalt bestimmen können.



![Rendered by QuickLaTeX.com = \left[\frac{1}{4}x^4-3x^3+13x^2-24x\right]\limits_2^3+ \left[-\frac{1}{4}x^4+3x^3-13x^2+24x\right]\limits_3^4](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f1a3d7b50caa8b4f785ea26ba59f9b4a_l3.png)

Merke: Statt bei jeder Integralrechnung zu überlegen, welches die obere und welches die untere Funktion ist, kannst du die Integralrechnung auch mit Betragstrichen aufstellen. Berechne dazu einfach in jedem Abschnitt 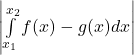 und addiere die Ergebnisse.
und addiere die Ergebnisse.
Rotationskörper
Auch beim Thema Rotationskörper spielt die Integralrechnung eine wichtige Rolle. Ein Rotationskörper entsteht, wenn du eine Fläche im Koordinatensystem (z.B. ein Dreieck) um eine der beiden Koordinatenachsen rotieren lässt.
Es gibt verschiedene Formeln, mit denen du jeweils das Volumen des Rotationskörpers oder seine Mantelfläche bei einer Drehung um die x-Achse bzw. um die y-Achse bestimmen kannst. Detailliert findest du alle Formeln und Beispiele in diesem Video .
Merke: In der Integralrechnung gibt es unterschiedliche Formeln für die Rotation um die x-Achse und die Rotation um die y-Achse! Pass auf, dass du die beiden nicht verwechselst!
Uneigentliche Integrale
Ein uneigentliches Integral
ist ein Integral, dessen Grenzen kritische Werte enthalten. Dafür gibt es zwei Möglichkeiten. Entweder sind die Integrationsgrenzen unbeschränkt, d.h.  oder
oder 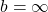 , oder
, oder  ist an den Integrationsgrenzen nicht definiert. Zur Berechnung eines uneigentlichen Integrals an seiner kritischen Grenze gehst du wie folgt vor.
ist an den Integrationsgrenzen nicht definiert. Zur Berechnung eines uneigentlichen Integrals an seiner kritischen Grenze gehst du wie folgt vor.
Anleitung: Uneigentliche Integrale berechnen
| Schritt 1: | Ersetze die kritische Grenze b durch eine Variable  : :
|
| Schritt 2: | Berechne das Integral in Abhängigkeit von  : :![Rendered by QuickLaTeX.com A(\beta) :=\int \limits_{a}^{\beta} f(x)dx = \left[F(x)\right]_{a}^{\beta}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eb8f39a4d4fbc83da8df3d6495c26f1a_l3.png)
|
| Schritt 3: | Bestimme, falls vorhanden, den Grenzwert:
|
Merke: Wenn du ein uneigentliches Integral mit zwei kritischen Grenzen gegeben hast, musst du es aufteilen und die beiden Limiten separat berechnen. Hier findest du weitere Aufgaben zum selber rechnen, damit du es noch besser verstehst.
Partielle Integration
Enthält die Integralrechnung ein Produkt, so gibt es ebenfalls eine spezielle Regel der Berechnung: Die partielle Integration. Hier wird sozusagen die Produktregel rückgängig gemacht. Es gilt die folgende Formel, die wir dir ausführlich mit vielen Beispielen in einem separaten Video erklären.
![Rendered by QuickLaTeX.com \int \limits_a^b f'(x) \cdot g(x) dx = \biggl[f(x) \cdot g(x)\biggr]\limits_a^b -\int\limits_a^b f(x)\cdot g'(x) dx.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3cc1214a2c938f888a0f318aed208803_l3.png)
Beispiel
Wir wollen  mittels partieller Integration berechnen. Hier ist
mittels partieller Integration berechnen. Hier ist  und
und  . Die Auswahl treffen wir so, dass das Integral im letzten Schritt, wenn wir
. Die Auswahl treffen wir so, dass das Integral im letzten Schritt, wenn wir  berechnen, wirklich einfacher wird. Damit gilt:
berechnen, wirklich einfacher wird. Damit gilt:
![Rendered by QuickLaTeX.com \int\limits_0^\pi x\cdot \sin(x)dx = \biggl[-x\cdot \cos(x)\biggr]\limits_0^\pi - \int\limits_0^\pi - \cos(x) dx = \pi +\sin(\pi)-\sin(0)=\pi.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b05627ee24ad931e87d2bfc2bb793999_l3.png)
Merke: Manchmal musst du bei einer Integralrechnung mehrmals partiell integrieren.
Merke: Entscheidend ist, dass du  und
und  richtig wählst. Die Merkhilfe LIATE erklären wir dir hier
ausführlich.
richtig wählst. Die Merkhilfe LIATE erklären wir dir hier
ausführlich.
Integration durch Substitution
Für die Integrationsregeln zur Substitution
haben wir ebenfalls ein eigenes, ausführliches Video für dich vorbereitet. Hier behandeln wir kurz die Formel und ein typisches Beispiel. Du verwendest die Substitutionsregel in der Integralrechnung ähnlich wie die Kettenregel beim Ableiten, also immer wenn du eine innere Funktion  und eine äußere Funktion
und eine äußere Funktion  gegeben hast, d.h. wenn
gegeben hast, d.h. wenn  . Substituierst du
. Substituierst du  , erhältst du
, erhältst du

Beispiel
Gesucht ist die die Lösung des Integrals  . Wir substituieren
. Wir substituieren  und erhalten durch Ableiten und Umstellen
und erhalten durch Ableiten und Umstellen  . Einsetzen in das Integral ergibt nach Anpassung der Integrationsgrenzen
. Einsetzen in das Integral ergibt nach Anpassung der Integrationsgrenzen
![Rendered by QuickLaTeX.com \int\limits_0^{\frac{\pi}{2}} \sin(2x)dx=\int\limits_0^\pi \sin(y)\cdot\frac{1}{2}dy = \biggl[\frac{-\cos(y)}{2}\biggr]\limits_0^\pi = 1.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3deabc6eabced95e8720f48db9c77ee8_l3.png)
Merke: Vergiss nicht, deine Integrationsgrenzen anzupassen, und das  richtig zu ersetzen!
richtig zu ersetzen!
Mittelwertsatz der Integralrechnung
Eine zentrale Aussage der Integralrechnung ist der Mittelwertsatz der Integralrechnung. Manchmal wird er auch als Cauchyscher Mittelwertsatz bezeichnet. Er existiert in verschiedenen Fassungen und erlaubt die Abschätzung von Integralen, ohne dass man sie explizit berechnen muss.
In der allgemeinen Fassung besagt der Mittelwertsatz der Integralrechnung, dass für ein stetiges ![Rendered by QuickLaTeX.com f:[a,b] \longrightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-53b3ffcd427ee67944ee48bf4315897a_l3.png) und ein integrierbares
und ein integrierbares ![Rendered by QuickLaTeX.com g:[a,b] \longrightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-db6815fd0acdc216a70ab0e8392d2025_l3.png) ohne Vorzeichenwechsel ein
ohne Vorzeichenwechsel ein ![Rendered by QuickLaTeX.com \xi \in [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c4f2ca3b42c3af09dc8fede13ef649b0_l3.png) existiert, sodass
existiert, sodass

Insbesondere für den Spezialfall  ergibt sich
ergibt sich
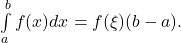
Geometrisch lässt sich dieser „erste Mittelwertsatz der Integralrechnung“ so interpretieren, dass zu jedem Flächeninhalt, den  mit der x-Achse einschließt, ein entsprechendes Rechteck mit derselben Fläche gefunden werden kann.
mit der x-Achse einschließt, ein entsprechendes Rechteck mit derselben Fläche gefunden werden kann.
Das ist insbesondere dann sehr praktisch, wenn du den durchschnittlichen Wert einer Funktion im Intervall ![Rendered by QuickLaTeX.com [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b7e4beaceae66bed938a06185209134a_l3.png) bestimmen möchtest. Dieser ist nämlich gerade
bestimmen möchtest. Dieser ist nämlich gerade  ! Wenn also nach dem Durchschnitt aller y-Werte im Intervall
! Wenn also nach dem Durchschnitt aller y-Werte im Intervall ![Rendered by QuickLaTeX.com [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b7e4beaceae66bed938a06185209134a_l3.png) gefragt ist, berechnest du
gefragt ist, berechnest du
![Rendered by QuickLaTeX.com f(\xi) = \frac{1}{b-a}\int\limits_a^b f(x)dx = \frac{1}{b-a}\left[F(b) - F(a)\right].](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7c2553184d5adeecc2e9e7defa23fa8c_l3.png)
Merke: Zentral wichtig ist bei dieser Integralrechnung, dass  im Intervall
im Intervall ![Rendered by QuickLaTeX.com [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b7e4beaceae66bed938a06185209134a_l3.png) keinen Vorzeichenwechsel enthält, d.h. dass
keinen Vorzeichenwechsel enthält, d.h. dass ![Rendered by QuickLaTeX.com g(x) < 0\quad \forall x \in [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fd2cae3241c372f2cee868e90dfe6183_l3.png) oder
oder ![Rendered by QuickLaTeX.com g(x) > 0 \quad\forall x \in [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eda00198c1d1719ba9c3c5ba62120bbf_l3.png) . Ohne diese Forderung ist der Satz im Allgemeinen nicht gültig!
. Ohne diese Forderung ist der Satz im Allgemeinen nicht gültig!
Kurvenintegrale
Bisher haben wir immer Integralrechnung nur für reelle Funktionen betrachtet. Mit dem Kurvenintegral
kann man auch über Funktionen integrieren, deren Definitionsmenge  eine Teilmenge des
eine Teilmenge des  ist. Entlang der Kurve
ist. Entlang der Kurve  , die diese Teilmenge umfasst, wird dann integriert.
, die diese Teilmenge umfasst, wird dann integriert.
Kurvenintegrale 1. Art sind Kurvenintegrale einer skalaren Funktion  . Sie ordnen jedem Wert
. Sie ordnen jedem Wert  eine reelle Zahl
eine reelle Zahl  zu.
zu.
Ist die Teilmenge  offen und
offen und ![Rendered by QuickLaTeX.com \gamma:[a,b]\rightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a6012a63f9060ef89fbb4daeda0beac9_l3.png) die Parametrisierung einer stückweise stetig differenzierbaren Kurve. Dann heißt
die Parametrisierung einer stückweise stetig differenzierbaren Kurve. Dann heißt

das Kurvenintegral 1. Art von  längs der Kurve
längs der Kurve  .
.
Analog dazu gibt es in der Integralrechnung das Kurvenintegral 2. Art für vektorwertige Funktionen. Wie genau es definiert ist und wie du es berechnest, erfährst du hier . Allgemein kannst du bei der Integralrechnung eines Kurvenintegrals folgendermaßen vorgehen.
Integralrechnung — häufigste Fragen
(ausklappen)
Integralrechnung — häufigste Fragen
(ausklappen)-
Wie erkenne ich, ob ich Substitution oder partielle Integration brauche?Substitution passt, wenn du eine äußere Funktion mit innerer Funktion und deren Ableitung erkennst. Partielle Integration passt, wenn im Integrand ein Produkt steht und Ableiten eines Faktors das Integral vereinfacht. Zum Beispiel ist
 typisch Substitution,
typisch Substitution,  typisch partielle Integration.
typisch partielle Integration.
-
Welche Fehler passieren oft beim bestimmten Integral mit negativen Flächen?Häufige Fehler sind, das Vorzeichen zu ignorieren oder Beträge zu früh zu setzen. Ein bestimmtes Integral liefert unter der x-Achse eine negative Zahl, der Flächeninhalt ist dagegen positiv und braucht Beträge und oft Teilintervalle. Zum Beispiel gilt für Fläche:
 .
.
-
Warum darf ich beim bestimmten Integral die Konstante c weglassen?Beim bestimmten Integral darf die Konstante
 weg, weil sie sich in
weg, weil sie sich in  immer aufhebt. Jede Stammfunktion hat die Form
immer aufhebt. Jede Stammfunktion hat die Form  , und beim Einsetzen entsteht
, und beim Einsetzen entsteht  . Deshalb ändert
. Deshalb ändert  das Ergebnis nicht.
das Ergebnis nicht.
-
Wie prüfe ich schnell, ob meine Stammfunktion richtig ist?Eine Stammfunktion ist richtig, wenn ihre Ableitung wieder genau den Integranden ergibt. Leite dazu
 ab und vergleiche das Ergebnis mit
ab und vergleiche das Ergebnis mit  , inklusive Vorzeichen und Faktoren. Zum Beispiel ist
, inklusive Vorzeichen und Faktoren. Zum Beispiel ist  korrekt zu
korrekt zu  , weil
, weil  .
.
-
Wann muss ich ein Integral in Teilintervalle aufteilen?Ein Integral muss in Teilintervalle aufgeteilt werden, wenn sich im Intervall das Vorzeichen von
 ändert oder sich die „obere“ und „untere“ Funktion wechselt. Dann berechnest du die Integrale getrennt und addierst passend (bei Flächen oft mit Beträgen). Zum Beispiel teilst du bei einer Nullstelle
ändert oder sich die „obere“ und „untere“ Funktion wechselt. Dann berechnest du die Integrale getrennt und addierst passend (bei Flächen oft mit Beträgen). Zum Beispiel teilst du bei einer Nullstelle  in
in ![Rendered by QuickLaTeX.com [a,x_0]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-3822869e00cb6188804366a828e4e271_l3.png) und
und ![Rendered by QuickLaTeX.com [x_0,b]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-a63d9814d0f43aa1e41e7566ba52d2d0_l3.png) .
.
Anleitung: Kurvenintegrale berechnen
| Schritt 1: | Parametrisiere die Kurve und setze sie in f ein. |
| Schritt 2: | Bestimme das Bogenelement ds. Es kann je nach Art des Kurvenintegrals skalar oder vektorwertig sein. |
| Schritt 3: | Berechne das Kurvenintegral. |