Linearisierung
Bei der Linearisierung einer Funktion f wird diese um eine Stelle  durch eine affin lineare Funktion g genähert. Das Verfahren zur Auffindung dieser Näherungsfunktion g wird auch als lineare Approximation bezeichnet. Da f lokal um eine Stelle
durch eine affin lineare Funktion g genähert. Das Verfahren zur Auffindung dieser Näherungsfunktion g wird auch als lineare Approximation bezeichnet. Da f lokal um eine Stelle  linearisiert wird, spricht man manchmal auch von lokaler Linearisierung bzw. lokaler linearer Approximation.
linearisiert wird, spricht man manchmal auch von lokaler Linearisierung bzw. lokaler linearer Approximation.
Inhaltsübersicht
Lineare Approximation und Ableitung
Um eine gute Näherung zu erhalten, muss der Funktionswert von g an der Stelle  auf jeden Fall dem Funktionswert von f an dieser Stelle entsprechen. Es muss also gelten:
auf jeden Fall dem Funktionswert von f an dieser Stelle entsprechen. Es muss also gelten:

Geradengleichung
Im Falle eindimensionaler reellwertiger Funktionen, die eine reelle Zahl wieder auf eine reelle Zahl abbilden, ist eine affin lineare Funktion g, die durch den Punkt  läuft, von folgender Form:
läuft, von folgender Form:

Der Graph von g ist eine Gerade, die durch den Punkt  läuft und die Steigung m besitzt. Wenn wir die Linearisierung eines Funktionsgraphens von f graphisch darstellen, sieht das folgendermaßen aus:
läuft und die Steigung m besitzt. Wenn wir die Linearisierung eines Funktionsgraphens von f graphisch darstellen, sieht das folgendermaßen aus:
Dabei verläuft f (weiß) an der Stelle  durch die Geraden g (blau) mit unterschiedlicher Steigung m.
durch die Geraden g (blau) mit unterschiedlicher Steigung m.
Für die beste lineare Approximation gilt es nun diejenige Steigung m zu finden, für die der Graph von g um die Stelle  möglichst gut zum Graphen von f passt. Mit anderen Worten: Die Graphen von f und g sollten in der Nähe von
möglichst gut zum Graphen von f passt. Mit anderen Worten: Die Graphen von f und g sollten in der Nähe von  nicht weit auseinander liegen, d.h. die Differenz zwischen f und g sollte möglichst klein sein.
nicht weit auseinander liegen, d.h. die Differenz zwischen f und g sollte möglichst klein sein.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Restfunktion
Diese Differenz wird in Abhängigkeit von der Stelle x, an der sie betrachtet wird, als Restfunktion

bezeichnet.
Hier siehst du die lineare Approximation des Graphen von f (weiß) um die Stelle  durch eine Gerade g (gelb) mit eingezeichneter Restfunktion r (weiß):
durch eine Gerade g (gelb) mit eingezeichneter Restfunktion r (weiß):
Durch Einsetzen der Funktionsgleichung von g ergibt sich:

Da die lineare Approximation vor allem in der Nähe von  gut sein soll, wird das Verhalten der Restfunktion r(x) für den Grenzfall
gut sein soll, wird das Verhalten der Restfunktion r(x) für den Grenzfall  betrachtet:
betrachtet:
![Rendered by QuickLaTeX.com \lim\limits_{x\to\ x_0} r(x)=\lim\limits_{x\to\ x_0} [f(x)-f(x_0)-m\cdot (x-x_0)]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d65a796c67ff5c5ba206428ceb475702_l3.png)
Dieser Grenzwert ergibt allerdings unabhängig von der Steigung m für stetige Funktionen f immer den Wert 0. Für in  stetige Funktionen gilt nämlich
stetige Funktionen gilt nämlich

und offensichtlich gilt außerdem
 .
.
Auf diese Art lässt sich also nicht untersuchen, für welche Steigung m die affin lineare Funktion g besonders gut die Ausgangsfunktion f nähert.
Zur genaueren Untersuchung eignet sich hingegen der folgende Grenzwert:

Durch Einsetzen der Restfunktion r(x) ergibt sich folgender Ausdruck:

Differenzierbarkeit
Ist die Funktion f an der Stelle  differenzierbar, so existiert der Grenzwert
differenzierbar, so existiert der Grenzwert  , der in diesem Ausdruck auftaucht. Dieser ist gerade der Differentialquotient
bzw. die Ableitung
, der in diesem Ausdruck auftaucht. Dieser ist gerade der Differentialquotient
bzw. die Ableitung  von f an der Stelle
von f an der Stelle  . Ist also f an der Stelle
. Ist also f an der Stelle  differenzierbar, so gilt:
differenzierbar, so gilt:

Dieser Ausdruck verschwindet genau dann, wenn die Steigung m der Linearisierung g gerade die Ableitung  von f an der Stelle
von f an der Stelle  ist. Man erhält also zwischen der Linearisierung
ist. Man erhält also zwischen der Linearisierung
 und der Differenzierbarkeit folgenden Zusammenhang:
und der Differenzierbarkeit folgenden Zusammenhang:
Eine eindimensionale reellwertige Funktion f lässt sich genau dann um die Stelle  linearisieren, wenn sie dort differenzierbar ist. Das ist der Fall, wenn es eine Konstante m gibt, sodass gilt:
linearisieren, wenn sie dort differenzierbar ist. Das ist der Fall, wenn es eine Konstante m gibt, sodass gilt:

Häufig zu sehen ist auch eine andere Schreibweise dieser Bedingung, welche man erhält, indem man x durch  ersetzt. Dadurch wird aus dem Grenzübergang
ersetzt. Dadurch wird aus dem Grenzübergang  der Übergang
der Übergang  und die gesamte Bedingung lautet:
und die gesamte Bedingung lautet:

Ist f in  differenzierbar, so ist die Konstante m gerade die Ableitung
differenzierbar, so ist die Konstante m gerade die Ableitung  von f an der Stelle
von f an der Stelle  .
.
Tangentialebene
Wird eine reellwertige Funktion betrachtet, die von zwei Variablen x und y abhängt, so stellt der Graph der Linearisierung g die Tangentialebene an den dreidimensionalen Graphen von f dar. In diesem Fall lautet die Funktionsgleichung von g nämlich:


Diese Gleichung stellt eine typische Ebenengleichung dar.
Durch Betrachtung der Funktionsgleichung der Linearisierung g wird ersichtlich, dass diese stets genau das Taylorpolynom bis zum linearen Glied darstellt.
Linearisierung einer DGL
Linearisierung kann auch im Bereich der Differentialgleichungen
von Nutzen sein. Häufig ist es nämlich möglich eine DGL (Differentialgleichung) zu linearisieren, um die Auffindung ihrer Lösung dadurch zu vereinfachen. Die DGL wird dabei um ihre Ruhelage bzw. den Arbeitspunkt linearisiert.
Ein Beispiel hierfür ist die Linearisierung der Bewegungsgleichung eines Pendels:

Hier kann nämlich  für kleine Winkel
für kleine Winkel  , also um die Stelle
, also um die Stelle  durch die Funktion
durch die Funktion

genähert werden. Die DGL vereinfacht sich dann zu:

Linearisierung — häufigste Fragen
(ausklappen)
Linearisierung — häufigste Fragen
(ausklappen)-
Woran merke ich an einem Graphen, dass eine Funktion bei x₀ nicht linearisierbar ist?Du erkennst Nicht-Linearisierbarkeit daran, dass es bei x₀ keine eindeutige Tangente gibt. Typische Graph-Merkmale sind eine Ecke (Knick), eine Spitze oder eine senkrechte Tangente mit unendlicher Steigung. Zum Beispiel ist
 bei
bei  nicht linearisierbar.
nicht linearisierbar.
-
Wie entscheide ich, wie nah x an x₀ sein muss, damit die Linearisierung noch eine gute Näherung ist?Du wählst x so nah an x₀, dass die Krümmung kaum sichtbar ist und der Fehler klein bleibt. Praktisch prüfst du mehrere Abstände h und vergleichst
 mit deiner Toleranz. Wird der Fehler beim Halbieren von h deutlich kleiner, bist du nah genug.
mit deiner Toleranz. Wird der Fehler beim Halbieren von h deutlich kleiner, bist du nah genug.
-
Welche typischen Rechenfehler passieren bei g(x)=f(x₀)+f'(x₀)·(x−x₀) am häufigsten?Am häufigsten werden
 und
und  verwechselt oder
verwechselt oder  nicht korrekt eingesetzt. Außerdem geht oft ein Vorzeichen in
nicht korrekt eingesetzt. Außerdem geht oft ein Vorzeichen in  verloren oder
verloren oder  wird als Funktion
wird als Funktion  stehen gelassen. Ein Klassiker ist auch,
stehen gelassen. Ein Klassiker ist auch,  fälschlich zu
fälschlich zu  zu machen.
zu machen.
-
Wie unterscheide ich Linearisierung und Taylorpolynom 2. Ordnung, wenn beide als Näherung benutzt werden?Die Linearisierung nutzt nur Funktionswert und erste Ableitung, das Taylorpolynom 2. Ordnung zusätzlich die zweite Ableitung. Deshalb enthält das Taylorpolynom einen quadratischen Term. Konkret: Linearisierung
 , Taylor 2. Ordnung
, Taylor 2. Ordnung  .
.
-
Wie rechne ich die Tangentialebene aus, wenn ich f(x,y) als Formel gegeben habe, aber bei partiellen Ableitungen oft durcheinanderkomme?Die Tangentialebene bei
 ist
ist  . Dabei heißt
. Dabei heißt  : nach x ableiten und y wie eine Konstante behandeln, und bei
: nach x ableiten und y wie eine Konstante behandeln, und bei  umgekehrt. Setze danach erst
umgekehrt. Setze danach erst  ein.
ein.
Beispiel – Linearisierung einer Funktion
Die Linearisierung einer Funktion f soll am Beispiel der Wurzelfunktion  illustriert werden. Diese soll um die Stelle
illustriert werden. Diese soll um die Stelle  linear approximiert werden. Dazu wird zunächst die Ableitung
linear approximiert werden. Dazu wird zunächst die Ableitung ![Rendered by QuickLaTeX.com f' (x_0)=\frac{1}{\sqrt[2]{x_0}} =\frac{1}{6}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c9262a4fd0943880324c3f3c9a73a148_l3.png) bestimmt und anschließend dieser Wert sowie
bestimmt und anschließend dieser Wert sowie  und
und  in die Gleichung
in die Gleichung

eingesetzt. Die Linearisierung bzw. die Tagentengleichung von f an der Stelle  lautet also:
lautet also:

Mit dieser Funktion g(x) wird die Wurzelfunktion  um die Stelle
um die Stelle  also am besten genähert.
also am besten genähert.
Es gilt beispielsweise:  und
und  . Die Lineare Approximation der Wurzelfunktion durch die Funktion g(x) ist also auch an der Stelle x=10 noch relativ gut.
. Die Lineare Approximation der Wurzelfunktion durch die Funktion g(x) ist also auch an der Stelle x=10 noch relativ gut.
Es soll im Folgenden noch die Differenzierbarkeit der Wurzelfunktion an der Stelle  mithilfe der Linearisierung g(x) gezeigt werden.
mithilfe der Linearisierung g(x) gezeigt werden.
Die Restfunktion r(x) lautet in diesem Beispiel:

Der für die Differenzierbarkeit zu untersuchende Grenzwert lautet demnach:

Durch Erweitern des linken Quotienten um den Faktor  vereinfacht sich dieser Ausdruck gemäß:
vereinfacht sich dieser Ausdruck gemäß:
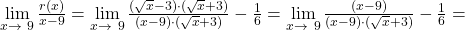

So wurde also nochmal explizit überprüft, dass die Wurzelfunktion an der Stelle  differenzierbar ist und die Ableitung
differenzierbar ist und die Ableitung  besitzt.
besitzt.


