Partielle Ableitungen
Bei der partiellen Ableitung werden Funktionen betrachtet, die eine Teilmenge des  nach
nach  abbilden. Dabei wird eine solche Funktion, die von mehreren Variablen abhängt, nach nur einer dieser Variablen abgeleitet. Dazu werden die restlichen Variablen als Konstanten angesehen und die Funktion dadurch als Funktion einer Variablen betrachtet.
abbilden. Dabei wird eine solche Funktion, die von mehreren Variablen abhängt, nach nur einer dieser Variablen abgeleitet. Dazu werden die restlichen Variablen als Konstanten angesehen und die Funktion dadurch als Funktion einer Variablen betrachtet.
Inhaltsübersicht
Schreibweisen der partiellen Ableitungen
In der gerade erfolgten Definition wurde eine Schreibweise der partiellen Ableitung benutzt, welche vom Symbol  Gebrauch macht. Dieses wird als „d“ oder auch als „del“ gesprochen. Äquivalente Schreibweisen bzw. Symbole der i-ten partiellen Ableitung in
Gebrauch macht. Dieses wird als „d“ oder auch als „del“ gesprochen. Äquivalente Schreibweisen bzw. Symbole der i-ten partiellen Ableitung in  lauten:
lauten:



Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Partiell ableiten
Eine Funktion  nach der i-ten Variable
nach der i-ten Variable  partiell abzuleiten funktioniert, wie eingangs erwähnt, recht simpel. Man sieht alle anderen Variablen als Konstanten an. Dadurch kann die Funktion als Funktion der Variablen
partiell abzuleiten funktioniert, wie eingangs erwähnt, recht simpel. Man sieht alle anderen Variablen als Konstanten an. Dadurch kann die Funktion als Funktion der Variablen  angesehen werden. Die partielle Ableitung entspricht der gewöhnlichen Ableitung
dieser Funktion.
angesehen werden. Die partielle Ableitung entspricht der gewöhnlichen Ableitung
dieser Funktion.
Partiell ableiten: Beispiel 1
Beispielsweise soll die partielle Ableitung der Funktion  nach der ersten Variablen
nach der ersten Variablen  bestimmt werden. Dabei können dann die Variablen
bestimmt werden. Dabei können dann die Variablen  und
und  als konstant betrachtet werden. Die partielle Ableitung nach
als konstant betrachtet werden. Die partielle Ableitung nach  lautet demnach:
lautet demnach:

Analog ergeben sich die partiellen Ableitungen nach den anderen beiden Variablen:


Partiell ableiten: Beispiel 2
Betrachtet man Funktionen, welche von maximal drei Variablen abhängen, werden diese häufig nicht mit  bezeichnet, sondern mit x, y und z. Ein solcher Fall soll im folgenden Beispiel behandelt werden: Betrachtet wird die Funktion
bezeichnet, sondern mit x, y und z. Ein solcher Fall soll im folgenden Beispiel behandelt werden: Betrachtet wird die Funktion  Die partiellen Ableitungen nach x bzw. nach y lauten:
Die partiellen Ableitungen nach x bzw. nach y lauten:


Deutung der partiellen Ableitungen
Die Bedeutung der partiellen Ableitungen einer Funktion  die von den zwei Variablen x und y abhängt, lässt sich noch geometrisch interpretieren. Der Graph dieser Funktion lässt sich nämlich als Hügelfläche im Dreidimensionalen darstellen. Die partielle Ableitung nach x an der Stelle
die von den zwei Variablen x und y abhängt, lässt sich noch geometrisch interpretieren. Der Graph dieser Funktion lässt sich nämlich als Hügelfläche im Dreidimensionalen darstellen. Die partielle Ableitung nach x an der Stelle  gibt dann die Steigung des Graphen an dieser Stelle an, wenn man sich von dort aus in positive x-Richtung bewegt. Man kann sich das auch folgendermaßen vorstellen: Wird der Funktionsgraph von
gibt dann die Steigung des Graphen an dieser Stelle an, wenn man sich von dort aus in positive x-Richtung bewegt. Man kann sich das auch folgendermaßen vorstellen: Wird der Funktionsgraph von  mit einer Ebene geschnitten, die den Punkt
mit einer Ebene geschnitten, die den Punkt  enthält und parallel zur
enthält und parallel zur  –
– -Ebene liegt, so ergibt sich eine Schnittkurve. Die partielle Ableitung nach x an der Stelle
-Ebene liegt, so ergibt sich eine Schnittkurve. Die partielle Ableitung nach x an der Stelle  ist dann gerade die Steigung der Tangente an dieser Schnittkurve.
ist dann gerade die Steigung der Tangente an dieser Schnittkurve.
Für Funktionen, die von mehr als zwei Variablen abhängen, hält die geometrische Interpretation allerdings nicht mehr stand. Man kann hier die partielle Ableitung nach der i-ten Variable als die Änderungsrate des Funktionswertes an der Stelle  interpretieren, wenn man eine kleine Veränderung der i-ten Variable betrachtet.
interpretieren, wenn man eine kleine Veränderung der i-ten Variable betrachtet.
Partielle Ableitungen höherer Ordnung
Partielle Ableitungen 1. Ordnung
Die bisher definierten partiellen Ableitungen einer Funktion werden auch als partielle Ableitungen 1. Ordnung bezeichnet. Ist die Funktion  auf dem ganzen Definitionsbereich
auf dem ganzen Definitionsbereich  partiell differenzierbar nach der i-ten Variable, so lässt sich die partielle Ableitungsfunktion ganz einfach wie folgt definieren:
partiell differenzierbar nach der i-ten Variable, so lässt sich die partielle Ableitungsfunktion ganz einfach wie folgt definieren:

Partielle Ableitungen 2. Ordnung
Diese Funktion kann wiederum partiell nach einer Variablen 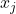 abgeleitet werden. Diese partielle Ableitung wird dann Partielle Ableitung 2. Ordnung genannt und mit folgender Schreibweise abgekürzt:
abgeleitet werden. Diese partielle Ableitung wird dann Partielle Ableitung 2. Ordnung genannt und mit folgender Schreibweise abgekürzt:

Wird zweimal hintereinander die partielle Ableitung nach derselben Variablen  gebildet, wird das folgendermaßen notiert:
gebildet, wird das folgendermaßen notiert:

Über die Vertauschbarkeit der zweiten Ableitungen macht der Satz von Schwarz eine Aussage: Ist  eine zweimal stetig partiell differenzierbare Funktion, so gilt für alle
eine zweimal stetig partiell differenzierbare Funktion, so gilt für alle  :
:

Zur Verdeutlichung werden im Folgenden alle ersten und zweiten partiellen Ableitungen der Funktion  aus Beispiel 2 aufgelistet:
aus Beispiel 2 aufgelistet:






Man sieht also, dass gilt: 
Ableitungsregeln
Wie bereits erwähnt, entspricht das partielle Ableiten nach der i-ten Variable genau dem herkömmlichen Ableiten, wenn die üblichen Variablen als Konstanten betrachtet werden. Daher gelten auch die üblichen Ableitungsregeln.
Summenregel
Für  gilt:
gilt:

Beispielsweise gilt für  :
:


Produktregel
Für  gilt:
gilt:

Beispielsweise gilt für  :
:


Quotientenregel
Für  gilt:
gilt:

Beispielsweise gilt für  :
:


Partielle Ableitungen — häufigste Fragen
(ausklappen)
Partielle Ableitungen — häufigste Fragen
(ausklappen)-
Was mache ich bei einer partiellen Ableitung mit den anderen Variablen, die ich gerade nicht ableite?Du behandelst alle anderen Variablen beim partiellen Ableiten wie Konstanten. Dadurch wird die mehrvariable Funktion beim Ableiten nach einer Variable wie eine normale Ein-Variablen-Funktion gerechnet. Zum Beispiel ist bei
 nach
nach  dann
dann  und
und  konstant.
konstant.
-
Wann heißt eine Funktion in einem Punkt partiell differenzierbar nach einer Variable?Eine Funktion heißt in
 partiell differenzierbar nach
partiell differenzierbar nach  , wenn der Grenzwert des Differenzenquotienten existiert. Konkret muss
, wenn der Grenzwert des Differenzenquotienten existiert. Konkret muss  existieren. Dieser Grenzwert ist dann die partielle Ableitung
existieren. Dieser Grenzwert ist dann die partielle Ableitung  .
.
-
Welche Schreibweisen für partielle Ableitungen kann ich in Aufgaben sehen?In Aufgaben sind mehrere gleichbedeutende Schreibweisen üblich:
 ,
,  ,
,  und
und  . Alle meinen dieselbe Ableitung, nämlich die partielle Ableitung von
. Alle meinen dieselbe Ableitung, nämlich die partielle Ableitung von  nach der i-ten Variablen, ausgewertet an der Stelle
nach der i-ten Variablen, ausgewertet an der Stelle  .
.
-
Wie kann ich mir die partielle Ableitung bei f(x,y) als Steigung am Graphen vorstellen?Die partielle Ableitung nach x an
 ist die Steigung des Graphen dort in positiver x-Richtung. Das liegt daran, dass du y festhältst und nur x veränderst. Anschaulich entsteht eine Schnittkurve, wenn du den Graphen mit einer Ebene parallel zur x-
ist die Steigung des Graphen dort in positiver x-Richtung. Das liegt daran, dass du y festhältst und nur x veränderst. Anschaulich entsteht eine Schnittkurve, wenn du den Graphen mit einer Ebene parallel zur x- -Ebene schneidest, und die Ableitung ist die Tangentensteigung dieser Kurve.
-Ebene schneidest, und die Ableitung ist die Tangentensteigung dieser Kurve.
-
Wann darf ich bei gemischten zweiten partiellen Ableitungen die Reihenfolge vertauschen?Du darfst die Reihenfolge gemischter zweiter partieller Ableitungen vertauschen, wenn die Funktion zweimal stetig partiell differenzierbar ist. Dann gilt nach dem Satz von Schwarz für alle Variablen
 und
und  :
:  .
.
Kettenregel
Für  gilt:
gilt:

Beispielsweise gilt für  :
:


 offen und
offen und  eine reelwertige Funktion. Sei weiterhin
eine reelwertige Funktion. Sei weiterhin  ein Punkt aus
ein Punkt aus 
