Video

Quiz

Satz von Stokes

Wichtige Inhalte in diesem Video

Allgemeiner Integralsatz von Stokes

Satz von Stokes Beispiel Zylindermantel

In diesem Artikel wird der Satz von Stokes behandelt. Dabei wird zunächst der allgemeine Stokessche Satz formuliert bevor kurz auf dessen Spezialfälle den Hauptsatz der Differential- und Integralrechnung (HDI) sowie den Gaußschen Integralsatz eingegangen wird. Darüber hinaus soll der klassische Integralsatz von Stokes als weiterer Spezialfall des allgemeinen etwas genauer beleuchtet werden. Abschließend erfolgt die Berechnung zweier Beispiele.

Doch du musst nicht unbedingt den ganzen Artikel lesen, um das Wichtigste rund um den Satz von Stokes zu erfahren. Dafür haben wir nämlich ein extra Video erstellt, dass dich einfach und unkompliziert in kürzester Zeit bestens informiert.

Inhaltsübersicht

Allgemeiner Integralsatz von Stokes

im Videozur Stelle im Video springen

Wenn vom Satz von Stokes die Rede ist, so ist damit in den meisten Fällen der klassische Stokessche Integralsatz gemeint. Er stellt einen Spezialfall des allgemeinen Integralsatzes von Stokes dar, welcher wie folgt lautet:

Sei $U \subset \mathbb{R}^n$ offen und $M \subset U$ eine orientierte -dimensionale Untermannigfaltigkeit mit $k \geq 2$ sowie $\omega$ eine stetig differenzierbare -Form in . Dann gilt für jede kompakte Menge $A\subset M$ mit glattem Rand

$\int_A d\omega=\int{\partial A}\omega$ ,

wobei $\partial A$ die induzierte Orientierung trägt und $d\omega$ die äußere Ableitung von $\omega$ bezeichnet.

Zugrundeliegendes topologisches Prinzip

Dem Satz von Stokes liegt das topologische Prinzip zugrunde, dass bei der Pflasterung eines Flächenstücks durch gleichorientierte „Pflastersteine“ die inneren Wege in entgegengesetzter Richtung durchlaufen werden, was dazu führt, dass sich ihre Beiträge zum Linienintegral gegenseitig aufheben und nur noch der Beitrag der Randkurve übrig bleibt.

Hauptsatz der Differential- und Integralrechnung als Spezialfall

Für n=1 entartet der allgemeine Integralsatz von Stokes zum Hauptsatz der Differential- und Integralrechnung: Sei $(a,b)\subset\mathbb{R}$ ein offenes Intervall und $f:[a,b]\rightarrow\mathbb{R}$ eine stetig differenzierbare Funktion. Dann gilt:

$\int_{a}^{b}{df\left(x\right)=\int_{a}^{b}{f^\prime\left(x\right)dx=f\left(x\right)|_a^b}}$

Integralsatz von Gauß als Spezialfall

Als weiterer Spezialfall folgt aus dem allgemeinen Integralsatz von Stokes der Gaußsche Integralsatz. Um das zu zeigen wird k=n gewählt und es sei

$\omega=\sum \limits_{i=1}^n(-1)^{i-1}f_idx_1\land...\land\widehat{dx_l}\land...\land dx_n$ ,

d.h. $\omega =f\cdot d\vec{S}$ mit dem stetig differenzierbaren Vektorfeld $f=(f_1,...,f_n): U\rightarrow \mathbb{R}$ . Dabei zeigt das Dach über dx_i an, dass dieser Faktor weggelassen werden muss. Sei außerdem $\nu: \partial A\rightarrow\mathbb{R}^n$ das äußere Einheits-Normalenfeld, so gilt

$\int_{\partial A}\omega=\int_{\partial A}{<f\left(x\right),\nu\left(x\right)>dS\left(x\right)}$

Mit $d\omega=\mathrm{div}(f)dx_1\land ...\land dx_n$ ergibt sich außerdem

$\int_{A}d\omega=\int_{A}\mathrm{div}f(x)d^nx$

Letztlich ergibt dies den Gaußschen Integralsatz

$\int_{A}\mathrm{div}f(x)d^nx=\int_{\partial A}{<f\left(x\right),\nu\left(x\right)>dS\left(x\right)}$

Satz von Stokes als klassischer Integralsatz von Stokes

Häufig und vor allem in technischen Studiengängen und der Physik ist die Rede vom Satz von Stokes. Hiermit ist in der Regel der klassische Integralsatz von Stokes gemeint, welcher auch Satz von Kelvin-Stokes oder Rotationssatz genannt wird. Gemeinsam mit dem Gaußschen Integralsatz spielt er eine wesentliche Rolle bei der Formulierung der Maxwell-Gleichungen in der Integralform.

Spezialfall des allgemeinen Integralsatzes von Stokes

Der klassische Satz von Stokes ergibt sich wie der HDI und der Gaußsche Integralsatz als Spezialfall des allgemeinen Integralsatzes von Stokes. In diesem Fall wird die offene Menge $U\subset \mathbb{R}^3$ sowie das stetig differenzierbare Vektorfeld $f:U\rightarrow \matbb{R}^3$ betrachtet. $N\subset U$ stelle eine zweidimensionale Untermannigfaltigkeit dar, dessen Orientierung durch das Einheits-Normalen-Feld $\nu:N\rightarrow\mathbb{R}^3$ gegeben sei. Auf der Untermannigfaltigkeit sei weiter ein Kompaktum gegeben, welches einen glatten Rand $\partial A$ besitze. Dieser wiederum sei durch das Einheits-Tangenten-Feld $\tau:\partial A\rightarrow\mathbb{R}^3$ orientiert. Mit der in stetig differenzierbaren Pfaffschen Form

$\omega:=f\cdot d\vec{s}=\sum \limits_{i=1}^{3}f_idx_i$

und

$d\omega:=\mathrm{rot}f\cdot d\vec{S}=\sum \limits_{i<j}\left(\frac{\partial f_j}{\partial x_i}-\frac{\partial f_i}{\partial x_j}\right)dx_i\land dx_j$

ergibt sich somit der Satz von Stokes:

$\int_{A}\mathrm{rot}f\cdot d\vec{S}=\int_{\partial A}f\cdot d\vec{s}$

In einer anderen Schreibweise lautet er:

$\int_{A}<\mathrm{rot}f,\nu>dS=\int_{\partial A}<f,\tau>ds$

Satz von Stokes Formulierung

Es lässt sich folgendes ablesen:

Der Satz von Stokes besagt, dass ein Flächenintegral über die Rotation eines Vektorfeldes unter bestimmten Voraussetzungen in ein geschlossenes Kurvenintegral über die zur Kurve tangentiale Komponente des Vektorfeldes umgewandelt werden kann. Die durchlaufene Kurve muss dabei dem Rand der betrachteten Fläche entsprechen.

Satz von Stokes Beweis

Im Folgenden soll der Satz von Stokes bewiesen werden. Für diesen Beweis wird allerdings eine kleine Bedingung an die Fläche gestellt. Diese soll der Graph einer Funktion z=g(x,y) sein, welche über einem Gebiet in der -Ebene definiert ist. Mit und $\partial P$ seien die Projektionen von und dem im Gegenuhrzeigersinn orientierten Rand $\partial A$ auf die -Ebene bezeichnet. $\partial A$ sei durch

$\vec{s}(t)=\left(x(t),y(t),g(x(t),y(t))\right)$

parametrisiert, woraus mithilfe der Kettenregel folgt:

$\vec{s}\thinspace'(t)=(x'(t),y'(t),g_x(x(t),y(t))\cdot x'(t)+g_y(x(t),y(t))\cdot y'(t))$

Das bedeutet für das im Satz von Stokes betrachtete Kurvenintegral:

$\int_{\partial A}f\cdot d\vec{s}=\int_{\partial A}f\cdot \vec{s}\thinspace'(t)dt=$

$\int_{\partial A}f_1(\vec{s}(t))\cdot x'(t)+f_2(\vec{s}(t))\cdot y'(t)+f_3(\vec{s}(t))$

$\cdot (g_x(x(t),y(t))\cdot x'(t)+g_y(x(t),y(t))\cdot y'(t))dt$

Durch Zusammenfassen ergibt sich:

$\int_{\partial A}f\cdot d\vec{s}=\int_{\partial A}[f_1(\vec{s}(t))+f_3(\vec{s}(t))\cdot g_x(x(t),y(t))]\cdot x'(t)$

$+[f_2(\vec{s}(t))+f_3(\vec{s}(t))\cdot g_y(x(t),y(t))]\cdot y'(t)dt$

Wird nun

$h_1(x,y):=f_1(x,y,g(x,y))+f_3(x,y,g(x,y))\cdot g_x(x,y)$

$h_2(x,y):=f_2(x,y,g(x,y))+f_3(x,y,g(x,y))\cdot g_y(x,y)$

gesetzt, so kann das Integral folgendermaßen geschrieben werden:

$\int_{\partial A}f\cdot d\vec{s}=\int_{\partial P}h_1(x,y)\cdot x'(t)+h_2(x,y)\cdot y'(t)dt$

Mit dem Satz von Green in der -Ebene kann dieses Integral umgeschrieben werden zu:

$\int_{\partial A}f\cdot d\vec{s}=\int_{P}\left[\frac{\partial h_2}{\partial x}-\frac{\partial h_1}{\partial y}\right]dxdy$

Da für die partiellen Ableitungen von h_1 und h_2 mithilfe der Ketten- und Produktregel

$\frac{\partial h_1}{\partial y}=\frac{\partial f_1}{\partial y}+\frac{\partial f_1}{\partial z}\cdot g_y+\left(\frac{\partial f_3}{\partial y}+\frac{\partial f_3}{\partial z}\cdot g_y\right)\cdot g_x+f_3\cdot g_{xy}$

$\frac{\partial h_2}{\partial x}=\frac{\partial f_2}{\partial x}+\frac{\partial f_2}{\partial z}\cdot g_x+\left(\frac{\partial f_3}{\partial x}+\frac{\partial f_3}{\partial z}\cdot g_x\right)\cdot g_y+f_3\cdot g_{yx}$

gilt, ergibt sich folgendes Integral:

$\int_{\partial A}f\cdot d\vec{s}=\int_{P}-g_x\left(\frac{\partial f_3}{\partial y}-\frac{\partial f_2}{\partial z}\right)-g_y\left(\frac{\partial f_1}{\partial z}-\frac{\partial f_3}{\partial x}\right)+1\left(\frac{\partial f_2}{\partial x}-\frac{\partial f_1}{y}\right)dxdy$

Für die andere Seite $\int_{A}\mathrm{rot}f\cdot d\vec{S}$ des Satzes von Stokes gilt in dem betrachteten Fall:

$\mathrm{rot}f=\left(\begin{matrix}\frac{\partial f_3}{\partial y}-\frac{\partial f_2}{\partial z}\\\frac{\partial f_1}{\partial z}-\frac{\partial f_3}{\partial x}\\\frac{\partial f_2}{\partial x}-\frac{\partial f_1}{\partial y}\\\end{matrix}\right)$

sowie

$d\vec{S}=\left(\begin{matrix}-g_x\\-g_y\\1\\\end{matrix}\right)dxdy$

Dadurch ist die Gleichheit der beiden Seiten und der Satz von Stokes für diesen Fall bewiesen:

$\int_{A}\mathrm{rot}f\cdot d\vec{S}=\int_{\partial A}f\cdot d\vec{s}$

Satz von Stokes Beispiel

Im Folgenden soll der Satz von Stokes beispielhaft für zwei gegebene Problemstellungen angewandt werden.

Satz von Stokes Beispiel Halbkugelschale

Im ersten Beispiel sei das Vektorfeld $f(x,y,z)= \left(\begin{matrix}z\\x\\y\\\end{matrix}\right)$ sowie die Halbkugelschale A: x^2+y^2+z^2=1 für $z\geq 0$ gegeben.

Um die Gleichheit der beiden Seiten im klassischen Integralsatz von Stokes zu zeigen, werden ein paar Vorarbeiten erledigt. Es lässt sich leicht nachrechnen, dass gilt:

$\mathrm{rot}f=\left(\begin{matrix}1\\1\\1\\\end{matrix}\right)$

Außerdem gilt für das Flächenelement $d\vec{S}$ in Kugelkoordinaten:

$d\vec{S}=\vec{e_r}dS=\left(\begin{matrix}\sin\vartheta\cdot \cos\varphi\\\sin\vartheta\cdot \sin\varphi\\\cos\vartheta\\\end{matrix}\right)\sin\vartheta \; d\varphi d\vartheta$

Die Randkurve $\partial A$ kann des Weiteren wie folgt parametrisiert werden:

$\partial A:t\rightarrow\vec{s}(t)=\left(\begin{matrix}\cos t\\\sin t\\0\\\end{matrix}\right)$ $t\in[0,2\pi]$

Somit ergibt sich für die eine Seite:

$\begin{align*}\int_{A}\mathrm{rot}f\cdot d\vec{S} &=\int_{0}^{\pi/2}\int_{0}^{2\pi}(\sin \vartheta\cdot \cos \varphi+\sin \vartheta\cdot \sin \varphi+\cos \vartheta)\sin \vartheta \; d\varphi d\vartheta \\ &=\int_{0}^{\pi/2}\int_{0}^{2\pi}\sin^2 \vartheta\cdot \cos \varphi+\sin^2 \vartheta\cdot \sin \varphi + \cos \vartheta\sin \vartheta \; d\varphi d\vartheta \\ &= \int_{0}^{\pi/2} 0 + 0 + 2\pi \cdot \cos \vartheta\sin \vartheta \; d \vartheta \\ &= 2\pi \cdot \left[ \frac{1}{2} sin^2 \vartheta\right]_{\vartheta = 0}^{\pi/2} \\ &= \pi \end{align*}$

Die andere Seite berechnet sich zu:

$\int_{\partial A}f\cdot d\vec{s}=\int_{0}^{2\pi}f(\vec{s}(t))dt=\int_{0}^{2\pi}\left(\begin{matrix}0\\\cos t\\\sin t\\\end{matrix}\right)\cdot \left(\begin{matrix}-\sin t\\\cos t\\0\\\end{matrix}\right)dt=$

$\int_{0}^{2\pi}\cos^2 t\thinspace dt=\pi$

Somit ist gezeigt, dass die separate Berechnung beider Seiten zum selben Ergebnis führt.

Da die Kreisscheibe $A:\vec{s}(r,\varphi)=\left(\begin{matrix}r\cdot \cos \varphi\\r\cdot \sin \varphi\\0\\\end{matrix}\right)$ mit $0\leq r\leq 1$ und $0\leq \varphi\leq 2\pi$ den selben Rand $\partial A$ besitzt wie die eben betrachtete Halbkugelschale, ist auch der Wert des Integrals $\int_{\partial A}f\cdot d\vec{s}=\int_{A}\mathrm{rot}f\cdot d\vec{S}$ derselbe.

Quiz zum Thema Satz von Stokes

Satz von Stokes Beispiel Zylindermantel

im Videozur Stelle im Video springen

Im zweiten Beispiel soll der Fluss der Rotation des Vektorfeldes 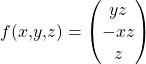$f(x,y,z)= \left(\begin{matrix}yz\\-xz\\z\\\end{matrix}\right)$ von innen nach außen durch den Zylindermantel A: x^2+y^2=1 für $0\leq z\leq 1$ berechnet werden. Hierzu wird nach dem klassichen Stokesschen Satz das Kurvenintegral entlang des Randes $\partial A$ von über das Vektorfeld bestimmt.

Das Kurvenintegral $\int_{\partial A}f\cdot d\vec{s}$ teilt sich auf in das Integral über die obere Umrandung C_O und die untere Umrandung C_U des Zylindermantels.

Diese werden wie folgt parametrisiert:

$C_O:t\rightarrow \vec{s_O}(t)=\left(\begin{matrix}\cos (-t)\\\sin (-t)\\0\\\end{matrix}\right)$ $t\in[0,2\pi]$

$C_U:t\rightarrow \vec{s_U}(t)=\left(\begin{matrix}\cos (t)\\\sin (t)\\0\\\end{matrix}\right)$ $t\in[0,2\pi]$

Somit berechnet sich der Fluss der Rotation von durch zu:

$\int_{A}\mathrm{rot}f\cdot d\vec{S}=\int_{\partial A}f\cdot d\vec{s}=\int_{C_O}f\cdot d\vec{s}+\int_{C_U}f\cdot d\vec{s}=$

$=\int_{0}^{2\pi}f(\vec{s_O}(t))\cdot \vec{s_O}'(t)dt+\int_{0}^{2\pi}f(\vec{s_U}(t))\cdot \vec{s_U}'(t)dt$

$=\int_{0}^{2\pi}\left(\begin{matrix}\sin (-t)\\-\cos (-t)\\1\\\end{matrix}\right)\cdot \left(\begin{matrix}\sin (-t)\\-\cos (-t)\\0\\\end{matrix}\right)dt+\int_{0}^{2\pi}\left(\begin{matrix}0\\0\\0\\\end{matrix}\right)\cdot \left(\begin{matrix}-\sin (t)\\\cos (t)\\0\\\end{matrix}\right)dt$

$=[1]_{0}^{2\pi}+0=2\pi$

zur Videoseite: Satz von Stokes

Beliebte Inhalte aus dem Bereich Analysis

Kurvenintegral

Dauer: 05:03

Polarkoordinaten

Zylinderkoordinaten

Kugelkoordinaten

Satz von Stokes

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .