Uneigentliche Integrale
In diesem Artikel erklären wir dir, was uneigentliche Integrale sind und zeigen dir anhand einer Reihe von Aufgaben, wie du sie berechnen kannst.
Du möchtest wissen, wie man uneigentliche Integrale berechnet, aber hast nur wenig Zeit? Dann schau dir unser Video dazu an. Hier wird dir alles Wichtige in kürzester Zeit erklärt.
Inhaltsübersicht
Uneigentliche Integrale einfach erklärt
Es gibt zwei Arten uneigentlicher Integrale  :
:
-
Erster Art: Die Integrationsgrenzen sind unbeschränkt. Das heißt
 und/oder
und/oder  sind gleich
sind gleich  oder
oder  .
. -
Zweiter Art:
 ist an den Integrationsgrenzen nicht definiert. Das heißt
ist an den Integrationsgrenzen nicht definiert. Das heißt  und/oder
und/oder  ist nicht definiert.
ist nicht definiert.
Generell sind also uneigentliche Integrale, solche mit kritischen Werten in den Grenzen.
Uneigentliche Integrale berechnen
Ein uneigentliches Integral mit nur einer kritischen Grenze  kann folgendermaßen berechnet werden:
kann folgendermaßen berechnet werden:
1.) Ersetze die kritische Grenze  durch eine Variable
durch eine Variable  :
:
 .
.
2.) Berechne das Integral in Abhängigkeit von  :
:
![Rendered by QuickLaTeX.com A(\beta) :=\int \limits_{a}^{\beta} f(x)dx = \left[F(x)\right]_{a}^{\beta}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5a0eabd678ccded533f31296a5bf9995_l3.png)
mit  als Stammfunktion von
als Stammfunktion von  .
.
3.) Bestimme, falls vorhanden, den Grenzwert  .
.
Analog kann auch das uneigentliche Integral mit  als kritische Grenze berechnet werden, indem sie durch eine Variable
als kritische Grenze berechnet werden, indem sie durch eine Variable  ersetzt wird. Das heißt, berechne
ersetzt wird. Das heißt, berechne

und anschließend den Grenzwert
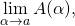
falls  für
für  konvergiert.
konvergiert.
Für ein uneigentliches Integral mit zwei kritischen Grenzen  und
und  muss dieses in zwei Integrale mit jeweils einer kritischen Grenze aufgeteilt werden:
muss dieses in zwei Integrale mit jeweils einer kritischen Grenze aufgeteilt werden:

wobei  gilt.
gilt.
Dann berechnen wir das erste uneigentliche Integral mit  als kritischer Grenze, sowie das zweite mit
als kritischer Grenze, sowie das zweite mit  als kritischer Grenze entsprechend dem obigen Verfahren. Anschließend werden die Ergebnisse addiert.
als kritischer Grenze entsprechend dem obigen Verfahren. Anschließend werden die Ergebnisse addiert.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Aufgabe 1
Überprüfe, ob das uneigentliche Integral

einen endlichen Wert besitzt.
Lösung:
Es handelt sich hier um ein uneigentliches Integral erster Art. Wir gehen im Folgenden die drei Schritte zur Berechnung durch.
1.) Die obere Integralgrenze  wird durch eine Variable
wird durch eine Variable  ersetzt:
ersetzt:

2.) Berechne das Integral in Abhängigkeit von  :
:

![Rendered by QuickLaTeX.com = \left[-\frac{1}{2} e^{-2x+1}\right]_{1/2}^{\beta}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2db2e7061fde7da37134b5d73bfa23ec_l3.png)

3.) Bilde den Grenzwert für 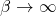 :
:

Der Grenzwert ergibt sich, da  gilt.
gilt.
Damit erhalten wir als Lösung:

Aufgabe 2
Überprüfe, ob das uneigentliche Integral

einen endlichen Wert besitzt.
Lösung:
Es ist ein uneigentliches Integral erster Art.
1.) Ersetze  durch eine Variable
durch eine Variable  :
:

2.) Wir berechnen das Integral in Abhängigkeit von  . Da im Zähler des Bruchs die Ableitung des Nenners steht, erhalten wir den Logarithmus
. Da im Zähler des Bruchs die Ableitung des Nenners steht, erhalten wir den Logarithmus  als Stammfunktion:
als Stammfunktion:
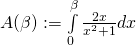
![Rendered by QuickLaTeX.com =\left[\ln(x^2+1)\right]\limits_{0}^{\beta}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-70880a6afeca84111e7b6845c4137182_l3.png)


3.) Nun müssen wir den Limes bilden

Jedoch konvergiert  in diesem Fall nicht
in diesem Fall nicht

da

Das uneigentliche Integral hat keinen endlichen Wert.
Dieses Beispiel zeigt, dass man mit der Anschauung der endlichen Fläche vorsichtig sein muss. Denn die Skizze lässt vermuten, dass die Fläche zwischen dem Graphen und der x-Achse endlich ist. Tatsächlich ist dies jedoch nicht der Fall, wie die Berechnung zeigt.
Aufgabe 3
Überprüfe, ob das uneigentliche Integral

einen endlichen Wert besitzt.
Lösung:
Es handelt sich hierbei um ein uneigentliches Integral zweiter Art. Denn die zu integrierende Funktion ist für  nicht definiert.
nicht definiert.
1.) Ersetze daher die untere Integrationsgrenze durch eine Variable  :
:

2.) Berechne das Integral in Abhängigkeit von  :
:

![Rendered by QuickLaTeX.com = \left[-\frac{1}{2x}\right] \limits_{\alpha}^{4}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7a0a2fc303c3c4734cc663c7082e8926_l3.png)

3.) Bestimme nun den Grenzwert

Allerdings konvergiert hier  gegen keinen endlichen Wert, da
gegen keinen endlichen Wert, da

gilt. Deshalb besitzt das uneigentliche Integral keinen endlichen Wert als Lösung.
Aufgabe 4
Überprüfe, ob das uneigentliche Integral

einen endlichen Wert besitzt.
Lösung:
Das ist ein uneigentliches Integral erster Art mit zwei kritischen Integralgrenzen. In diesem Fall muss das Integral in zwei Integrale mit jeweils einer kritischen Grenze aufgeteilt werden:
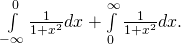
Wir beginnen damit, das erste uneigentliche Integral

zu bestimmen.
1.) Ersetze die kritische Intervallgrenze  durch eine Variable
durch eine Variable  :
:

2.) Bestimme das Integral in Abhängigkeit von  :
:

![Rendered by QuickLaTeX.com = \left[ \arctan(x)\right]_{\alpha}^{0}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d1aedf9fd8caba4f27c9eb24c37769ff_l3.png)


3.) Bestimme den Grenzwert für  :
:

Das bedeutet für das erste uneigentliche Integral gilt:

Nun müssen wir noch den Wert des zweiten uneigentlichen Integrals

bestimmen.
1.) Ersetze die kritische Intervallgrenze  durch die Variable
durch die Variable  :
:

2.) Bestimme das Integral in Abhängigkeit von  :
:

![Rendered by QuickLaTeX.com = \left[ \arctan(x)\right]_{0}^{\beta}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d426be1004486665bb73c88826d56224_l3.png)

3.) Bestimme den Grenzwert für 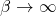 :
:

Damit gilt:

Schließlich addieren wir die Ergebnisse, um den Wert des gesuchten uneigentlichen Integrals zu erhalten:
