Grenzwert
Die Grenzwerte bestimmen gehört zu jeder Kurvendiskussion. Wie das funktioniert und was es zu beachten gibt, erfährst du hier! Schaue dir auch unser passendes Video an.
Inhaltsübersicht
Grenzwerte berechnen einfach erklärt
Um dir eine Funktion besser vorstellen zu können, hilft es oft, sie zu zeichnen. Häufig kannst du dein Koordinatensystem gar nicht groß genug machen und ein Teil des Graphen ist nicht zu sehen. Wie sieht der Graph außerhalb deiner Zeichnung aus? Diese Frage beantwortet der Grenzwert.
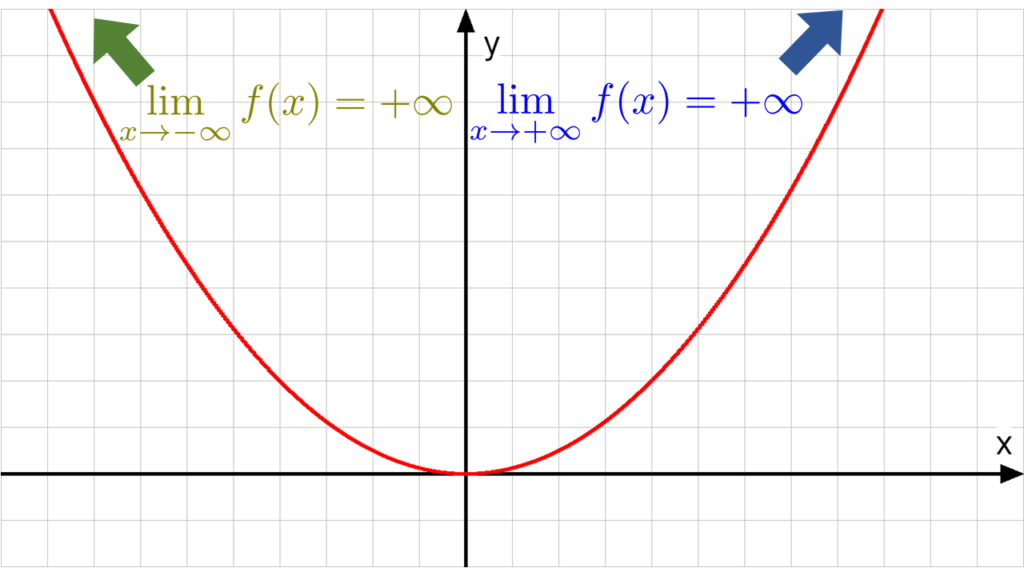
In der Abbildung siehst du den Graphen der Funktion 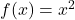 . Welche y-Werte bekommst du, wenn du immer größere (10, 100, 1000, …) und immer kleinere x-Werte (-10, -100, -1000, …) einsetzt? Hier kannst Du schon vermuten, dass in beiden Fällen immer größere y-Werte herauskommen.
. Welche y-Werte bekommst du, wenn du immer größere (10, 100, 1000, …) und immer kleinere x-Werte (-10, -100, -1000, …) einsetzt? Hier kannst Du schon vermuten, dass in beiden Fällen immer größere y-Werte herauskommen.
Der Limes (lim) sagt dir, was passiert, wenn x in eine bestimmte Richtung geht. Wenn du immer größere x-Werte in f einsetzt, schreibst du
![Rendered by QuickLaTeX.com \[ \lim\limits_{x\rightarrow +\infty} x^2 = +\infty \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-1c1a8505742a8035f3db0eb0dada0304_l3.png)
und umgekehrt für kleinere Zahlen
![Rendered by QuickLaTeX.com \[ \lim\limits_{x\rightarrow -\infty} x^2 = +\infty \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-698cf39421a3b76272b52b2ab80316ac_l3.png)
Verhalten im Unendlichen
Das Verhalten im Unendlichen
sagt dir also, in welche Richtung deine Funktion geht, wenn deine x-Werte nach unendlich (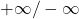 ) gehen. Schauen wir uns noch mal die Funktion
) gehen. Schauen wir uns noch mal die Funktion 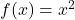 an.
an.
Limes gegen plus unendlich
Wie findest du die Grenzwerte ohne dir die Funktion aufzuzeichnen? Du kannst eine Wertetabelle erstellen:
| x | 1 | 5 | 10 | 50 | 100 |
| f(x) | 1 | 25 | 100 | 2.500 | 10.000 |
Wenn Du x=1 in deine Funktion einsetzt, bekommst du auch 1 heraus. Für 5 ist dein Funktionswert 25 und bei 10 steigt deine Funktion schon auf 100 an. f(50) ist 2.500 und für 100 bekommst du sogar 10.000.
Du kannst natürlich auch noch größere Zahlen einsetzen, aber du siehst bereits: Je größer die x-Werte sind, desto größer werden die y-Werte. In Mathe sagst du das so: Wenn x gegen plus unendlich geht ( ), geht f(x) auch gegen plus unendlich (
), geht f(x) auch gegen plus unendlich (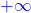 ).
).
Dafür gibt es auch eine Kurzschreibweise: den Limes. Schreibe zuerst das Wort lim. Darunter kommt dann, welche x-Werte du in deine Funktion einsetzt ( ). Hinter lim schreibst du deine Funktion f(x). Zuletzt noch ein Ist-Gleich-Zeichen und der Grenzwert, den du bestimmt hast:
). Hinter lim schreibst du deine Funktion f(x). Zuletzt noch ein Ist-Gleich-Zeichen und der Grenzwert, den du bestimmt hast:
![Rendered by QuickLaTeX.com \[ \lim\limits_{\textcolor{red}{x\rightarrow +\infty}} \textcolor{olive}{x^2} = \textcolor{blue}{+\infty} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0f8a81885b393442c845a14de2277962_l3.png)
Gesprochen: Der Limes von x2 für x gegen plus unendlich ist gleich plus unendlich.
Limes gegen minus unendlich
Damit hast du das Verhalten von f(x) im positiv Unendlichen ermittelt. Dasselbe kannst du auch für negative Zahlen machen. Erstelle eine Wertetabelle, um den Grenzwert bestimmen zu können:
| x | -1 | -5 | -10 | -50 | -100 |
| ex | 1 | 25 | 100 | 2.500 | 10.000 |
Wenn Du x=-1 in deine Funktion einsetzt bekommst du +1 heraus. Für -5 ist dein Funktionswert 25 und bei -10 steigt deine Funktion schon auf 100 an. f(-50) ist 2.500 und für -100 bekommst du sogar 10.000.
Du erkennst sofort, dass auch hier die y-Werte größer werden. Mathematisch korrekt sagst du also: Wenn x gegen minus unendlich geht ( ), geht f(x) gegen plus unendlich (
), geht f(x) gegen plus unendlich ( ). Die passende Limesschreibweise sieht dann so aus: Die eingesetzten x-Werte (
). Die passende Limesschreibweise sieht dann so aus: Die eingesetzten x-Werte ( ) kommen unter das Wort lim, deine Funktion (x2) rechts vom lim und der Grenzwert (
) kommen unter das Wort lim, deine Funktion (x2) rechts vom lim und der Grenzwert ( ) kommt hinter das Ist-Gleich-Zeichen.
) kommt hinter das Ist-Gleich-Zeichen.
![Rendered by QuickLaTeX.com \[ \lim\limits_{\textcolor{red}{x\rightarrow -\infty}} \textcolor{olive}{x^2} = \textcolor{blue}{+\infty} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c516a00c635afa1938253213c6285bdf_l3.png)
Gesprochen: Der Limes von x2 für x gegen minus unendlich ist gleich plus unendlich.
Das war es auch schon. So bestimmst du für eine Funktion ihr Verhalten im Unendlichen.
Das x mit dem meisten Einfluss bestimmt den Grenzwert der gesamten Funktion:
- x im Exponent (z.B. ex) → sehr viel Einfluss
- x mit höchstem Exponenten (z.B. x3)
- x ohne Exponent
- x in der Wurzel → sehr wenig Einfluss
Beispiel Grenzwerte bestimmen: e-Funktion
Damit du mit dem Limes-berechnen keine Probleme hast, haben wir dir noch ein zweites Beispiel vorbereitet. Welches Verhalten im Unendlichen hat die Funktion e hoch x?
Limes gegen plus unendlich
Fange wieder mit einer Wertetabelle an:
| x | 1 | 2 | 5 | 10 | 15 |
| ex | ~2,7 | ~7,4 | ~148 | ~22.026 | 3.269.017 |
Du siehst, dass ex sehr schnell sehr groß wird: e1 ist ungefähr 2,7, e2 ist circa 7,4. Für x=5 steigt ex schon auf 148 und e10 ist größer als 20.000. Bei x=15 ist der Funktionswert schon größer als 3 Millionen. Wenn x gegen unendlich geht ( ), geht ex also auch gegen unendlich (
), geht ex also auch gegen unendlich ( ).
).
![Rendered by QuickLaTeX.com \[ \lim\limits_{\textcolor{red}{x\rightarrow +\infty}} \textcolor{olive}{e^x} = \textcolor{blue}{+\infty} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d6e036a8d35a0640c2911f9c996801ac_l3.png)
Gesprochen: Der Limes von e hoch x für x gegen plus unendlich ist gleich plus unendlich.
Limes gegen minus unendlich
Doch wie ist es, wenn x gegen minus unendlich geht? Die Wertetabelle sieht dann so aus:
| x | -1 | -2 | -3 | -4 | -5 |
| ex | ~0,4 | ~0,1 | ~0,05 | ~0,02 | ~0,007 |
Für x=-1 bekommst Du einen y-Wert von 0,4. e-2 ist dagegen 0,1 und e-3 ist mit 0,05 noch kleiner. Bei noch kleineren Zahlen wie -4 und -5 liefert ex 0,02 und 0,007. Mit sinkenden x-Werten nähern sich die y-Werte als der Zahl 0 an. Das heißt, wenn x gegen minus unendlich geht ( ), dann geht ex gegen 0.
), dann geht ex gegen 0.
![Rendered by QuickLaTeX.com \[ \lim\limits_{\textcolor{red}{x\rightarrow -\infty}} \textcolor{olive}{e^x} = \textcolor{blue}{0} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-bceaad873dc90537ab2ead5ea2338c53_l3.png)
Gesprochen: Der Limes von e hoch x für x gegen minus unendlich ist gleich 0.
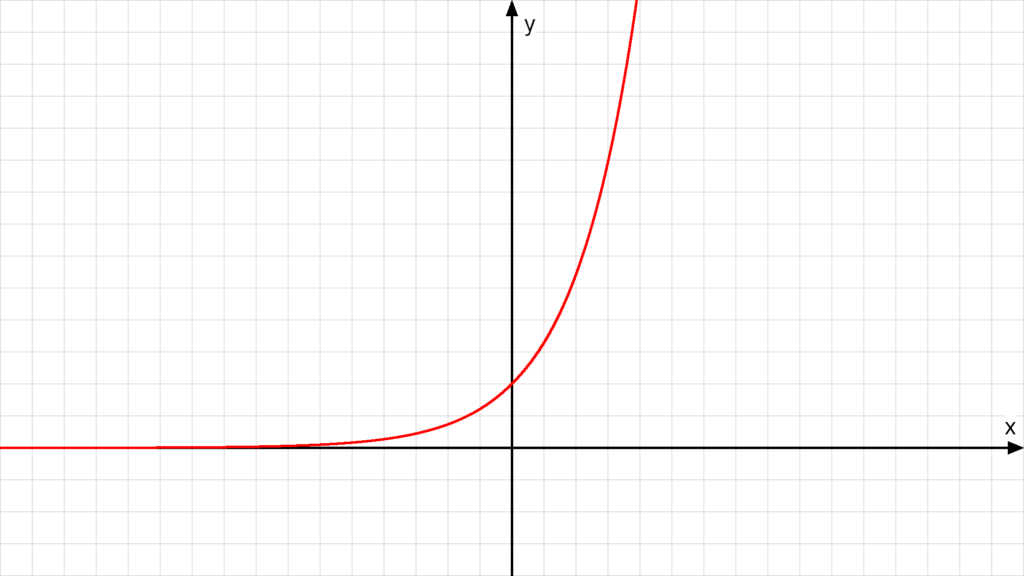
Wenn du dir den Graph von ex anschaust, siehst du auch, dass er von 0 kommt und nach plus unendlich geht.
Verhalten an Polstellen (links und rechtsseitiger Grenzwert)
Mit dem Grenzwert kannst du nicht nur das Verhalten im Unendlichen bestimmen. Gebrochen-Rationale Funktionen
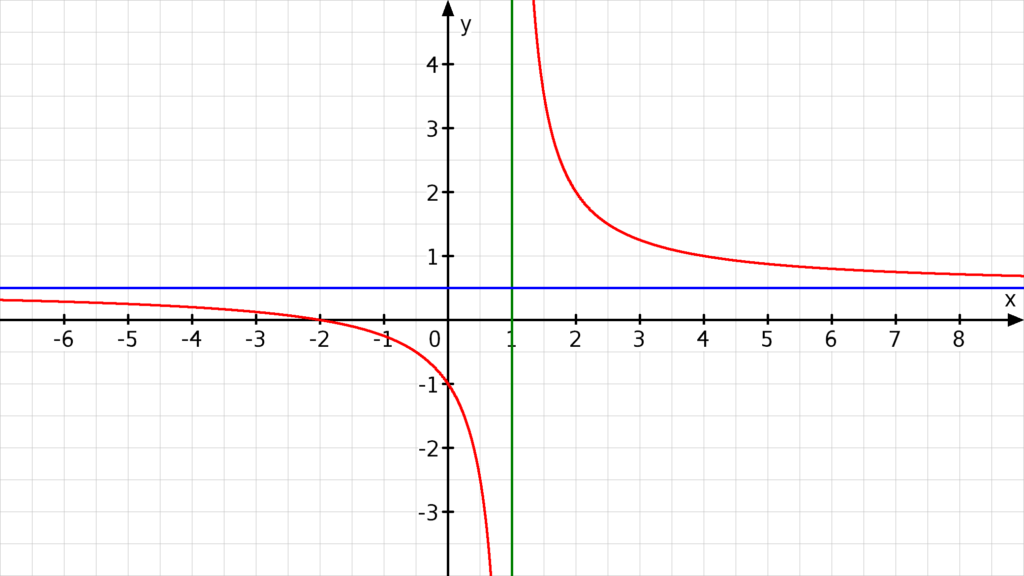
gehen auch für bestimmte endliche Zahlen ins Unendliche. Schaue dir zum Beispiel die Funktion 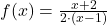 an. Wie du weißt, darfst du einen Bruch mit 0 im Nenner nicht ausrechnen. Daher kannst du hier 1 nicht einsetzen, weil du sonst durch 0 teilen müsstest. Dort hast du also eine Polstelle (grüne senkrechte Linie). An Polstellen lohnt es sich immer die Grenzwerte zu bestimmen.
an. Wie du weißt, darfst du einen Bruch mit 0 im Nenner nicht ausrechnen. Daher kannst du hier 1 nicht einsetzen, weil du sonst durch 0 teilen müsstest. Dort hast du also eine Polstelle (grüne senkrechte Linie). An Polstellen lohnt es sich immer die Grenzwerte zu bestimmen.
Wenn du eine Polstelle bei x=p hast, kannst du zwei verschiedene Grenzwerte bestimmen:
- Der rechtsseitige Grenzwert sagt dir, wohin die Funktion geht, wenn du dich der Polstelle von großen x-Werten näherst (
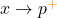 ). Mit dem „+„-Zeichen zeigst du, dass du dich von größeren Zahlen der Polstelle annäherst.
). Mit dem „+„-Zeichen zeigst du, dass du dich von größeren Zahlen der Polstelle annäherst. - Der linksseitige Grenzwert sagt dir, wohin die Funktion geht, wenn du dich von kleinen x-Werten näherst (
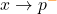 ). Mit dem „–„-Zeichen zeigst du, dass du dich von kleineren Zahlen der Polstelle annäherst.
). Mit dem „–„-Zeichen zeigst du, dass du dich von kleineren Zahlen der Polstelle annäherst.
Wenn du für den rechts- und linksseitigen Grenzwert das gleiche Ergebnis hast, nennst du diesen Grenzwert einen beidseitigen Grenzwert und schreibst  . Weil es bei einem beidseitigen Grenzwert egal ist, von welcher Richtung du dich näherst, lässt du hier die „+“/“-„-Zeichen weg.
. Weil es bei einem beidseitigen Grenzwert egal ist, von welcher Richtung du dich näherst, lässt du hier die „+“/“-„-Zeichen weg.
Linksseitiger Grenzwert gegen 1
Auch an einer Polstelle kannst du mit einer Wertetabelle Grenzwerte bestimmen. f(x) hat eine Polstelle bei x=1. Fange mit dem linksseitigen Grenzwert an, indem du dich der Zahl 1 mit Zahlen näherst, die kleiner als 1 sind:
| x | 0 | 0,5 | 0,7 | 0,9 | 0,99 |
| f(x) | -1 | -2,5 | -4,5 | -14,5 | -149,5 |
Für x=0 bekommst du einen y-Wert von -1. Bei 0,5 sind es -2,5 und bei 0,7 schon -4,5. f(0,9) ist -14,5 und bei x=0,99 ist f(x) -149,5. Du merkst schnell, dass f(x) gegen minus unendlich (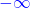 ) geht, wenn die x-Werte sich von unten der Zahl 1 nähern (
) geht, wenn die x-Werte sich von unten der Zahl 1 nähern ( ).
).
![Rendered by QuickLaTeX.com \[ \lim\limits_{\textcolor{red}{x\rightarrow 1^{\textcolor{orange}{-}}}} \textcolor{olive}{ \frac{x+2}{2\cdot (x-1)} } = \textcolor{blue}{-\infty} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-79b3c8b006b3ef586ed13bed1467c028_l3.png)
Gesprochen: Der linksseitige Limes von f(x) für x gegen 1 ist gleich minus unendlich.
Rechtsseitiger Grenzwert gegen 1
Als nächstes schaust du dir den rechtsseitigen Grenzwert an. Auch hier kannst du eine Wertetabelle benutzen. Was passiert, wenn du dich der Zahl 1 von größeren Werten näherst?
| x | 2 | 1,5 | 1,3 | 1,1 | 1,01 |
| f(x) | 2 | 3,5 | 5,5 | 15,5 | 150,5 |
Setzt du x=2 in deine Funktion ein, bekommst du wieder eine 2 heraus. Für 1,5 sind es 3,5 und bei 1,3 hast du einen Funktionswert von 5,5. f(1,1) ist schon 15,5 und bei 1,01 ist dein y-Wert 140,5. Du siehst: Je mehr du dich der Zahl 1 von größeren x-Werten näherst, desto größer werden deine y-Werte. Für x gegen 1 von größeren Werten ( ) geht f(x) gegen plus unendlich (
) geht f(x) gegen plus unendlich ( ).
).
![Rendered by QuickLaTeX.com \[ \lim\limits_{\textcolor{red}{x\rightarrow 1^{\textcolor{orange}{+}}}} \textcolor{olive}{ \frac{x+2}{2\cdot (x-1)} } = \textcolor{blue}{+\infty} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-30970ae097c969ffe4735f3ea870e7a0_l3.png)
Gesprochen: Der rechtsseitige Limes von f(x) für x gegen 1 ist gleich plus unendlich.
Grenzwerte bestimmen ist gar nicht so schwer, oder?
Linksseitiger Grenzwert gegen 0
Fange wieder mit einer Wertetabelle für den linksseitigen Grenzwert an. Setze dafür negative Zahlen in f(x), die immer näher bei 0 liegen:
| x | -1 | -0,5 | -0,25 | -0,1 | -0,01 |
| f(x) | 1 | 4 | 16 | 100 | 10.000 |
Für x=-1 erhältst du dann den y-Wert 1. Bei -0,5 sind es 4 und für -0,25 ist f(x) gleich 16. f(-0,1) ergibt schon 100 und f(-0,01) ist 10.000. Die Zahlen werden sehr schnell sehr groß. Du erkennst aber: Wenn x von kleinen Zahlen gegen 0 ( ) geht, geht f(x) gegen plus unendlich (
) geht, geht f(x) gegen plus unendlich ( ). Vergiss nicht das „–„-Zeichen, um zu zeigen, dass es sich um einen linksseitigen Limes handelt!
). Vergiss nicht das „–„-Zeichen, um zu zeigen, dass es sich um einen linksseitigen Limes handelt!
![Rendered by QuickLaTeX.com \[ \lim\limits_{ \textcolor{red}{x\rightarrow 0^{\textcolor{orange}{-}}} } \frac{1}{x^2} = \textcolor{blue}{+\infty} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-08ef7e9692b81b856b936f696f473154_l3.png)
Gesprochen: Der linksseitige Limes von 1 durch x-Quadrat für x gegen 0 ist gleich plus unendlich.
Rechtsseitiger Grenzwert gegen 0
Den rechtsseitigen Grenzwert bestimmst du auf die gleiche Weise wie den linksseitigen Grenzwert. Erstelle eine Wertetabelle, indem du positive Zahlen in f(x) einsetzt, die immer näher bei 0 liegen:
| x | 1 | 0,5 | 0,25 | 0,1 | 0,01 |
| f(x) | 1 | 4 | 16 | 100 | 10.000 |
Für x=1 erhältst du einen Funktionswert von 1. Bei f(0,5) ist 4 und für 0,25 erhältst du 16. Bei einem x-Wert von 0,1 ist dein y-Wert 100 und für 0,01 steigt die Funktion schon auf 10.000. Auch für den rechtsseitigen Grenzwert steigt die Funktion schnell ins unendliche: Wenn x von großen Zahlen gegen 0 ( ) geht, geht f(x) gegen plus unendlich (
) geht, geht f(x) gegen plus unendlich ( ). Vergiss nicht das „+„-Zeichen, um zu zeigen, dass es sich um einen rechtsseitigen Limes handelt!
). Vergiss nicht das „+„-Zeichen, um zu zeigen, dass es sich um einen rechtsseitigen Limes handelt!
![Rendered by QuickLaTeX.com \[ \lim\limits_{ \textcolor{red}{x\rightarrow 0^{\textcolor{orange}{+}}} } \textcolor{olive}{ \frac{1}{x^2} } = \textcolor{blue}{+\infty} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d35e59ac78af2eee000282c44f45aadb_l3.png)
Gesprochen: Der rechtsseitige Limes von 1 durch x-Quadrat für x gegen 0 ist gleich plus unendlich.
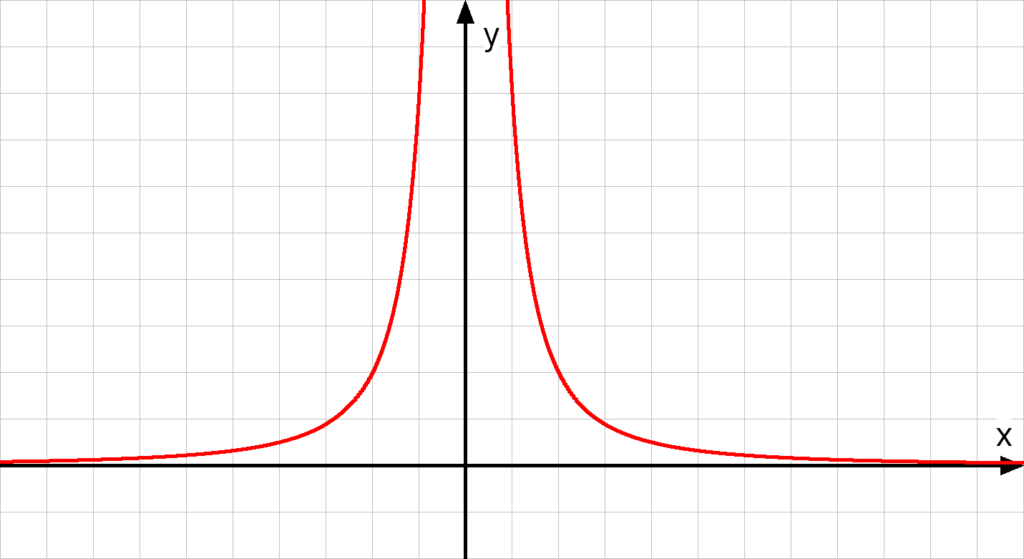
Beidseitiger Grenzwert gegen 0
Weil dein links- und rechtsseitiger Grenzwert gleich ist, kannst du beide auch zusammen als einen beidseitigen Grenzwert schreiben: Wenn x gegen 0 ( ) geht, geht f(x) gegen plus unendlich (
) geht, geht f(x) gegen plus unendlich ( ). Hier brauchst du nicht mehr „+„- oder „–„-Zeichen zu schreiben, weil es egal ist, von welcher Seite du dich der Polstelle näherst. Beide Grenzwerte sind ja gleich.
). Hier brauchst du nicht mehr „+„- oder „–„-Zeichen zu schreiben, weil es egal ist, von welcher Seite du dich der Polstelle näherst. Beide Grenzwerte sind ja gleich.
![Rendered by QuickLaTeX.com \[ \lim\limits_{ \textcolor{red}{x\rightarrow 0} } \textcolor{olive}{\frac{1}{x^2}} = \textcolor{blue}{+\infty} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-dff8807a92768d8e9f83529988832dc2_l3.png)
Gesprochen: Der Limes von 1 durch x-Quadrat für x gegen 0 ist gleich plus unendlich.
Um einen Grenzwert zu bestimmen, gehst du so vor:
- Prüfe, ob du den Grenzwert gegen unendlich oder gegen eine Zahl (z.B. 2) suchst.
- Erstelle eine Wertetabelle mit großen x-Werten (z.B. 1.000.000) oder x-Werten nah an der Zahl (z.B. 2,001).
- Ließ den Grenzwert an den y-Werten ab.
Asymptoten bestimmen
Falls deine Funktion im Unendlichen einer Zahl annähert, anstatt ins Unendliche zu verschwinden, hat sie eine waagerechte Asymptote . Schaue dir unser Video dazu an, um herauszufinden, wie du auch alle andere Arten von Asymptoten finden kannst!
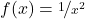 an. Sie hat bei x=0 eine Polstelle. Wie sieht der Graph in der Nähe von 0 aus?
an. Sie hat bei x=0 eine Polstelle. Wie sieht der Graph in der Nähe von 0 aus?