Sinusfunktion
In diesem Beitrag erklären wir dir, was die Sinusfunktion ist, welche Eigenschaften sie besitzt und welchen Einfluss verschiedene Parameter auf den Funktionsgraphen der Sinusfunktion haben.
Du bevorzugst Videos zum Lernen? Dann haben wir eine gute Nachricht für dich: Auch zum Thema Sinusfunktion haben wir ein animiertes Video – Klick drauf und genieße.
Inhaltsübersicht
Sinusfunktion einfach erklärt
Die Sinusfunktion ist, wie der Name bereits verrät, eine Funktion , genauer eine trigonometrische Funktion .
Du kannst dir die Sinusfunktion auch als eine Blackbox vorstellen, die irgendein Element aus den reellen Zahlen  frisst und ein anderes Element aus dem Intervall
frisst und ein anderes Element aus dem Intervall ![Rendered by QuickLaTeX.com [-1,1]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d3f435e3f121e6f6708a5146a75e662a_l3.png) ausspuckt.
ausspuckt.
Formal ausgedrückt, ist die Sinusfunktion folgende Abbildung:

Die Sinusfunktion ist eine Abbildung von der Menge  der reellen Zahlen in die Menge [-1,1], wobei sie ein Element
der reellen Zahlen in die Menge [-1,1], wobei sie ein Element  aus
aus  auf ein Element
auf ein Element  aus [-1,1] abbildet.
aus [-1,1] abbildet.
Sinusfunktion zeichnen
Lass uns doch der abstrakten Sinusfunktion eine anschauliche Gestalt geben. Hierzu nehmen wir eine kleine Wertetabelle auf, indem wir die  -Werte aus dem Intervall
-Werte aus dem Intervall ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) wählen und dazu die jeweiligen
wählen und dazu die jeweiligen  -Werte durch
-Werte durch  ausrechnen. Die Tabelle kann dann folgendermaßen aussehen:
ausrechnen. Die Tabelle kann dann folgendermaßen aussehen:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
0 | -0,5 | -0,866 | -1 | -0,866 | -0,5 | 0 | 0,5 | 0,866 | 1 | 0,866 | 0,5 | 0 |
Wenn wir nun diese Punkte in einem Koordinatensystem eintragen und miteinander verbinden, erhalten wir ein Bild wie das Folgende.
Die blauen Punkte stellen die Pärchen aus unserer Wertetabelle dar, die rote Kurve den tatsächlichen Funktionsgraphen der Sinusfunktion. Dieser Funktionsgraph wird auch Sinuskurve genannt. Außerhalb der  -Werte unserer Wertetabelle haben wir die Sinusfunktion aufgrund einer besonderen Eigenschaft dieser Funktion weiterzeichnen können. Diese Eigenschaften werden wir im nächsten Abschnitt vorstellen.
-Werte unserer Wertetabelle haben wir die Sinusfunktion aufgrund einer besonderen Eigenschaft dieser Funktion weiterzeichnen können. Diese Eigenschaften werden wir im nächsten Abschnitt vorstellen.
Die Sinusfunktion ist eine trigonometrische Funktion. Sie ordnet einem x-Wert seinen Sinuswert als y zu: y = sin(x). Du kannst die Sinuswerte auch am Einheitskreis ablesen. Das ist ein Kreis mit Radius 1.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Definitionsbereich und Wertebereich
Jede Abbildung besitzt einen Definitionsbereich
und einen Wertebereich
. Für  ist
ist
der Definitionsbereich = die Menge  der reellen Zahlen und
der reellen Zahlen und
der Wertebereich = die Menge [-1,1] aller reellen Zahlen von -1 bis 1.
Amplitude und Periode
Kommen wir nun zur Eigenschaft, die es uns ermöglicht hat, die Sinuskurve ohne Kenntnis der Werte außerhalb unserer Wertetabelle zeichnen zu können. Diese Eigenschaft ist die Periodizität
der Sinusfunktion. Das heißt, dass sich bei der Sinusfunktion ein gewisses Muster wiederholt. Das Muster entspricht genau dem Verlauf der Sinuskurve im Intervall von ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) . Du kannst also einfach das Muster in diesem Intervall nehmen, kopieren und dann so einfügen, dass der Graph verbunden bleibt. Und genau das haben wir bei der Konstruktion der Sinuskurve aus der Wertetabelle ausgenutzt. Die „Breite“ dieses Musters heißt Periode und ist für den Fall der Sinusfunktion
. Du kannst also einfach das Muster in diesem Intervall nehmen, kopieren und dann so einfügen, dass der Graph verbunden bleibt. Und genau das haben wir bei der Konstruktion der Sinuskurve aus der Wertetabelle ausgenutzt. Die „Breite“ dieses Musters heißt Periode und ist für den Fall der Sinusfunktion  .
.
Periode von  beträgt
beträgt  .
.
Du kannst an der Sinuskurve erkennen, dass die Sinusfunktion nie größer als +1 beziehungsweise kleiner als -1 wird. Diese „Barriere“ zwischen der die Werte der Sinusfunktion auf- und abschwingen heißt Amplitude und hier gilt
Amplitude  .
.
Symmetrie
Die Sinusfunktion ist eine ungerade Funktion. Das bedeutet, dass ihr Graph punktsymmetrisch zum Koordinatenursprung (0|0) ist. Für alle (reellen) Zahlen x kannst du dir somit merken:
sin(-x) = – sin(x)
Beispiel: sin(-π/2) = -1 = -sin(π/2)
Punktsymmetrie bedeutet, dass der Funktionsgraph links vom Ursprung durch Spiegelung des Funktionsgraphen rechts vom Ursprung am Punkt (0,0) erhalten werden kann. Formal gilt also allgemein
 .
.
Das Bild unten soll die Eigenschaften als eine Zusammenfassung illustrieren. Hier sollen die Pärchen (B, B‘) und (C, C‘) die Punktsymmetrie der Sinusfunktion veranschaulichen.
Sinusfunktion Nullstellen
Der periodische Charakter der Sinusfunktion erleichtert einige interessante Berechnungen. Da sich das Muster nach  wiederholt, reicht es beispielsweise für die Nullstellen der Sinusfunktion aus, sich nur auf das Intervall von
wiederholt, reicht es beispielsweise für die Nullstellen der Sinusfunktion aus, sich nur auf das Intervall von ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) zu konzentrieren. Alle anderen Nullstellen können wir aufgrund der Periodizität leicht ableiten. An der Sinuskurve erkennen wir, dass sich innerhalb von
zu konzentrieren. Alle anderen Nullstellen können wir aufgrund der Periodizität leicht ableiten. An der Sinuskurve erkennen wir, dass sich innerhalb von ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) die Nullstellen an den Stellen
die Nullstellen an den Stellen  und
und  befinden. Der Abstand zwischen zwei benachbarten Nullstellen ist also genau
befinden. Der Abstand zwischen zwei benachbarten Nullstellen ist also genau  . Die Periodizität der Sinusfunktion erlaubt uns daher die allgemeine Feststellung, dass gilt
. Die Periodizität der Sinusfunktion erlaubt uns daher die allgemeine Feststellung, dass gilt


Hier ist  ein Element der Menge
ein Element der Menge  der ganzen Zahlen.
der ganzen Zahlen.
Sinusfunktion Extremwerte
Auch für die Extremwerte der Sinusfunktion reicht die Betrachtung im Intervall ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) . Anhand der Sinuskurve können wir erkennen, dass die Funktion an der Stelle
. Anhand der Sinuskurve können wir erkennen, dass die Funktion an der Stelle  ein Minimum und an der Stelle
ein Minimum und an der Stelle  ein Maximum besitzt. Der Abstand zwischen zwei benachbarten Maxima beziehungsweise Minima ist genau
ein Maximum besitzt. Der Abstand zwischen zwei benachbarten Maxima beziehungsweise Minima ist genau  . Der periodische Charakter der Sinusfunktion lässt uns somit darauf schließen, dass die Minima und Maxima bei folgenden Werten liegen.
. Der periodische Charakter der Sinusfunktion lässt uns somit darauf schließen, dass die Minima und Maxima bei folgenden Werten liegen.
 und
und
 .
.
Auch hier ist  eine ganze Zahl. Manchmal findest du auch
eine ganze Zahl. Manchmal findest du auch
 .
.
Der einzige Unterschied zwischen  und
und  liegt darin, ob du das Intervall
liegt darin, ob du das Intervall ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) oder
oder ![Rendered by QuickLaTeX.com [0, 2\pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5d29727dde8ad3d69c29b7899bd923e0_l3.png) betrachtest.
betrachtest.
Sinusfunktion Ableiten
Die Sinusfunktion hat eine besonders einfache Ableitung. Es ist

Das heißt, die Ableitung der Sinusfunktion ist die Kosinusfunktion, die wieder eine periodische Funktion ist mit ähnlichen Eigenschaften wie die der Sinusfunktion.
Sinusfunktion integrieren
Auch das unbestimmte Integral der Sinusfunktion ist einfach. Es gilt
 .
.
Das unbestimmte Integral von  ist also auch wieder eine trigonometrische Funktion.
ist also auch wieder eine trigonometrische Funktion.
Sinusfunktion Parameter
Bisher haben wir die Sinusfunktion in der Form  besprochen. Das ist aber nur eine Spezialform der allgemeinen Form.
besprochen. Das ist aber nur eine Spezialform der allgemeinen Form.
 ,
,
wobei  und
und  beliebige reelle Zahlen sind.
beliebige reelle Zahlen sind.
In diesem Abschnitt erklären wir dir, welchen Einfluss jeder dieser sogenannten Parameter  und
und  auf die Gestalt der Sinuskurve hat.
auf die Gestalt der Sinuskurve hat.
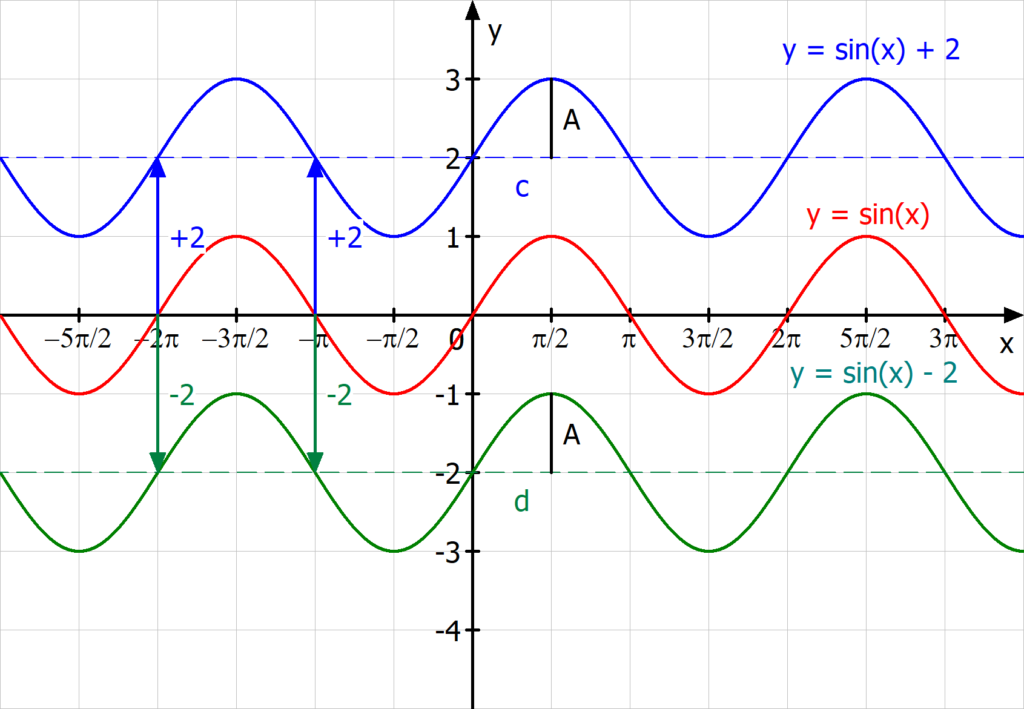
Sinusfunktion verschieben in y-Richtung (Parameter d)
Wir beginnen mit dem Einfluss von Parameter d. Dieser verschiebt je nach Vorzeichen die Sinuskurve nach oben ( ) beziehungsweise nach unten (
) beziehungsweise nach unten ( ). Das folgende Bild soll das illustrieren.
). Das folgende Bild soll das illustrieren.
In diesem Bild ist d einmal +2 und einmal -2. An jedem Punkt entlang der einfachen Sinuskurve (rot) wird 2 hinzuaddiert und es entsteht die blaue Kurve. Wird hingegen 2 subtrahiert entsteht die grüne Kurve. Beachte, dass der Parameter d auf die Amplitude A der Sinuskurve keinen Einfluss hat, denn auch die verschobenen Sinuskurven schwingen gleich auf und ab.
Sinusfunktion verschieben in x-Richtung (Parameter c)
Der Parameter c verschiebt die Sinuskurve entweder nach links ( ) oder nach rechts (
) oder nach rechts ( ). Die Vorzeichen sind im Fall der Verschiebung in x-Richtung leider nicht so intuitiv, wie im Fall der Verschiebung in y-Richtung. Bei einem positiven Parameterwert könntest du, in Analogie zur Verschiebung in y-Richtung, denken, dass die Sinuskurve nach rechts verschoben wird. Es passiert aber genau das Umgekehrte. Du kannst dir es auch so vorstellen, dass bei einem positiven Parameterwert c der Ursprung des Koordinatensystems nach rechts verschoben wird und die Sinuskurve dadurch nach links. Das Bild unten veranschaulicht das.
). Die Vorzeichen sind im Fall der Verschiebung in x-Richtung leider nicht so intuitiv, wie im Fall der Verschiebung in y-Richtung. Bei einem positiven Parameterwert könntest du, in Analogie zur Verschiebung in y-Richtung, denken, dass die Sinuskurve nach rechts verschoben wird. Es passiert aber genau das Umgekehrte. Du kannst dir es auch so vorstellen, dass bei einem positiven Parameterwert c der Ursprung des Koordinatensystems nach rechts verschoben wird und die Sinuskurve dadurch nach links. Das Bild unten veranschaulicht das.
Auch der Parameter c hat keinen Einfluss auf die Amplitude der Sinuskurve. In diesem Fall ist c =  und jeder Punkt entlang der originalen Kurve (rot) wird um
und jeder Punkt entlang der originalen Kurve (rot) wird um  nach rechts verschoben. Anhand dieses Beispiels kannst du erkennen, dass
nach rechts verschoben. Anhand dieses Beispiels kannst du erkennen, dass

gilt.
Streckung und Stauchung in y-Richtung (Parameter a)
Der Parameter a streckt ( ) beziehungsweise staucht (
) beziehungsweise staucht ( ) die Sinuskurve entlang der y-Richtung. Dieser Parameter hat also Einfluss auf die Amplitude der Sinuskurve. Die folgende Grafik illustriert das.
) die Sinuskurve entlang der y-Richtung. Dieser Parameter hat also Einfluss auf die Amplitude der Sinuskurve. Die folgende Grafik illustriert das.
Hier ist  die Amplitude der grünen Kurve und
die Amplitude der grünen Kurve und  die Amplitude der blauen Kurve. Im Fall der grünen Kurve wird jeder Punkt entlang der originalen Sinuskurve (rot) mit 0,5 multipliziert. Bei der blauen Kurve hingegen wird jeder Punkt mit 2 multipliziert. Ist das Vorzeichen des Parameters a negativ, so wird der Funktionsgraph zusätzlich entlang der
die Amplitude der blauen Kurve. Im Fall der grünen Kurve wird jeder Punkt entlang der originalen Sinuskurve (rot) mit 0,5 multipliziert. Bei der blauen Kurve hingegen wird jeder Punkt mit 2 multipliziert. Ist das Vorzeichen des Parameters a negativ, so wird der Funktionsgraph zusätzlich entlang der  -Achse gespiegelt.
-Achse gespiegelt.
Streckung und Stauchung in x-Richtung (Parameter b)
Zuletzt schauen wir uns den Einfluss des Parameters b an. Dieser streckt ( ) oder staucht (
) oder staucht ( ) die Sinuskurve entlang der x-Richtung. Das Bild unten stellt diese Situation graphisch dar.
) die Sinuskurve entlang der x-Richtung. Das Bild unten stellt diese Situation graphisch dar.
Beachte, dass auch der Parameter b keinen Einfluss auf die Amplitude der Sinuskurve hat. Hingegen hat dieser Parameter Einfluss darauf, wie schnell die Kurve auf- und abschwingt. Die Periode  einer um b gestreckten oder gestauchten Sinuskurve kannst du folgendermaßen ausrechnen.
einer um b gestreckten oder gestauchten Sinuskurve kannst du folgendermaßen ausrechnen.

Kombination verschiedener Parameter
Zum Abschluss dieses Abschnitts schauen wir uns den kombinierten Einfluss verschiedener Parameter an. Die folgende Grafik soll das für drei veränderte Sinuskurven exemplarisch illustrieren.
Die blaue Kurve beispielsweise ist eine um 1 nach oben verschobene, um den Faktor 3 in y-Richtung und um den Faktor 0,5 in x-Richtung gestreckte Version der originalen roten Kurve.
Sinusfunktion Aufgaben
Lass uns zum Schluss ein paar typische Aufgaben gemeinsam lösen. Die erste Aufgabe beinhaltet das Bestimmen der Funktionsvorschrift für eine gegebene Sinuskurve. Die zweite Aufgabe verlangt das Zeichnen einer Sinuskurve für eine gegebene Funktionsvorschrift und das Bestimmen der Nullstellen, Extremstellen und des Wertebereichs.
Aufgabe 2: Sinuskurve zeichnen und charakterisieren
Zeichne die Funktionsvorschrift

und bestimme ihren Wertebereich sowie die Nullstellen und Extremstellen im Intervall ![Rendered by QuickLaTeX.com [-2\pi, 2\pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7a9949db371f2e46bccd6959d9954291_l3.png) .
.
Lösungen
Aufgabe 1: Funktionsvorschrift aus Sinuskurve bestimmen
Die einfachste Methode ist sich eine unveränderte Sinuskurve gedanklich in diesem Diagramm vorzustellen. Das könnte folgendermaßen aussehen.
Im ersten Schritt bestimmen wir den Parameter d. Dazu betrachten wir die Nullstellen der gedanklichen Kurve und ermitteln, wie weit diese nach oben geschoben wurden. In diesem Fall sind die Nullstellen um +2 verschoben und damit ist  . Als nächstes bestimmen wir die Amplitude. Die rote Kurve schwingt mit +2 beziehungsweise -2 um die verschobenen Nullstellen. Die Amplitude ist somit 2 und es ist
. Als nächstes bestimmen wir die Amplitude. Die rote Kurve schwingt mit +2 beziehungsweise -2 um die verschobenen Nullstellen. Die Amplitude ist somit 2 und es ist  . Die Breite eines Musters der roten Kurve ist genau
. Die Breite eines Musters der roten Kurve ist genau  . Daher wurde die Kurve in x-Richtung weder gestreckt noch gestaucht und somit ist
. Daher wurde die Kurve in x-Richtung weder gestreckt noch gestaucht und somit ist  . Für den Parameter c schauen wir uns die Nullstelle der originalen Kurve im Ursprung an. Wir erkennen, dass diese um
. Für den Parameter c schauen wir uns die Nullstelle der originalen Kurve im Ursprung an. Wir erkennen, dass diese um  nach rechts verschoben wurde, denn ab
nach rechts verschoben wurde, denn ab  beginnt die rote Kurve das gleiche Muster wie die originale Kurve zu haben. Damit ist
beginnt die rote Kurve das gleiche Muster wie die originale Kurve zu haben. Damit ist  .
.
Wir haben nun alle Parameterwerte gefunden und müssen diese nur noch in die allgemeine Form der Sinusfunktion einsetzen. Wir erhalten dann


für die gesuchte Funktionsvorschrift.
Das folgende Bild soll die Schritte, die wir hier geschildert haben, illustrieren.
Sinusfunktion — häufigste Fragen
(ausklappen)
Sinusfunktion — häufigste Fragen
(ausklappen)-
Was bedeutet es, dass die Sinusfunktion Werte nur zwischen minus eins und eins hat?Dass die Sinusfunktion Werte nur zwischen -1 und 1 hat, bedeutet: Für jedes reelle
 liegt
liegt  immer im Intervall
immer im Intervall ![Rendered by QuickLaTeX.com [-1,1]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-d3f435e3f121e6f6708a5146a75e662a_l3.png) . Der Graph kann also nie über
. Der Graph kann also nie über  steigen und nie unter
steigen und nie unter  fallen. Diese Grenzen bilden den Wertebereich der Sinusfunktion.
fallen. Diese Grenzen bilden den Wertebereich der Sinusfunktion.
-
Wie zeichne ich die Sinuskurve mit einer Wertetabelle im Bereich von minus pi bis pi?Um die Sinuskurve im Bereich
![Rendered by QuickLaTeX.com [-\pi,\pi]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-85aeef0704e392045c401d8d5feeb72d_l3.png) mit einer Wertetabelle zu zeichnen, wählst du mehrere
mit einer Wertetabelle zu zeichnen, wählst du mehrere  -Werte in diesem Intervall und berechnest jeweils
-Werte in diesem Intervall und berechnest jeweils  . Beispiel: Für
. Beispiel: Für  ist
ist  , für
, für  ist
ist  und für
und für  ist
ist  .
.
-
Warum kann ich die Sinuskurve nach dem Intervall von minus pi bis pi einfach weiterzeichnen?Du kannst die Sinuskurve nach dem Intervall
![Rendered by QuickLaTeX.com [-\pi,\pi]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-85aeef0704e392045c401d8d5feeb72d_l3.png) weiterzeichnen, weil die Sinusfunktion periodisch ist. Das heißt, ihr Verlauf wiederholt sich als Muster immer wieder. Bei
weiterzeichnen, weil die Sinusfunktion periodisch ist. Das heißt, ihr Verlauf wiederholt sich als Muster immer wieder. Bei  hat dieses Muster die Breite
hat dieses Muster die Breite  , daher lässt sich der Graph durch Wiederholen verbunden fortsetzen.
, daher lässt sich der Graph durch Wiederholen verbunden fortsetzen.
-
Wie erkenne ich an der Sinuskurve die Periode und die Amplitude?An der Sinuskurve ist die Periode die horizontale Breite eines vollständigen sich wiederholenden Musters, bei
 also
also  . Die Amplitude ist die maximale Auslenkung nach oben und unten, also die „Barriere“ zwischen den Werten
. Die Amplitude ist die maximale Auslenkung nach oben und unten, also die „Barriere“ zwischen den Werten  und
und  . Beispiel: Die Kurve erreicht
. Beispiel: Die Kurve erreicht  und
und  , daher ist
, daher ist  .
.
-
Wie verändern a, b, c und d die Sinuskurve bei a mal sin von bx plus c plus d?Bei
 streckt oder staucht
streckt oder staucht  die Kurve in y-Richtung und bei negativem
die Kurve in y-Richtung und bei negativem  wird zusätzlich an der x-Achse gespiegelt.
wird zusätzlich an der x-Achse gespiegelt.  streckt oder staucht in x-Richtung und ändert die Periode zu
streckt oder staucht in x-Richtung und ändert die Periode zu  .
.  verschiebt in x-Richtung (bei
verschiebt in x-Richtung (bei  nach links, bei
nach links, bei  nach rechts) und
nach rechts) und  verschiebt in y-Richtung (hoch bei
verschiebt in y-Richtung (hoch bei  , runter bei
, runter bei  ).
).
Aufgabe 2: Sinuskurve zeichnen und charakterisieren
Wir erkennen, dass die originale Sinuskurve um 3 nach unten und um  nach links verschoben wurde. Der Ursprung der Kurve beginnt also im Punkt (-
nach links verschoben wurde. Der Ursprung der Kurve beginnt also im Punkt (- , -3). Die Amplitude wurde um den Faktor 3 gestreckt. Da hier
, -3). Die Amplitude wurde um den Faktor 3 gestreckt. Da hier  ist, ist die Periode unverändert gleich
ist, ist die Periode unverändert gleich  . Wir beginnen daher im Punkt (-
. Wir beginnen daher im Punkt (- , -3) die Sinuskurve zu zeichnen, wobei diese Kurve die Amplitude
, -3) die Sinuskurve zu zeichnen, wobei diese Kurve die Amplitude  besitzt. Das Ergebnis sieht dann wie folgt aus.
besitzt. Das Ergebnis sieht dann wie folgt aus.
Wir haben in diesem Bild bereits die Extremstellen mit  und
und  sowie die Nullstellen mit
sowie die Nullstellen mit  und
und  gekennzeichnet. Außerdem haben wir durch die grün gestrichelte Linie den interessanten Bereich von
gekennzeichnet. Außerdem haben wir durch die grün gestrichelte Linie den interessanten Bereich von ![Rendered by QuickLaTeX.com [-2\pi, 2\pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7a9949db371f2e46bccd6959d9954291_l3.png) dargestellt. Aus diesem Bild erkennen wir
dargestellt. Aus diesem Bild erkennen wir
Wertebereich = [0, -6],
Extremstellen bei  und
und  und
und
Nullstellen bei  und
und  .
.