Trigonometrische Funktionen
In diesem Beitrag zeigen wir dir, was trigonometrische Funktionen sind und welche wichtigen Eigenschaften trigonometrische Funktionen besitzen. Am Ende findest du Aufgaben zum Üben.
Du möchtest trigonometrische Funktionen schnellstmöglich erlernen? Dann schau dir unser Video zu diesem Thema an.
Inhaltsübersicht
Trigonometrische Funktionen einfach erklärt
Als trigonometrische Funktionen (auch Winkelfunktionen, seltener Kreisfunktionen) werden periodische Funktionen bezeichnet, die einen Input aufnehmen und einen Output liefern. Neben der Periodizität besitzen trigonometrische Funktionen weitere wichtige Eigenschaften. Erst diese Eigenschaften machen die Funktionen zu trigonometrische Funktionen.
In diesem Beitrag unterscheiden wir folgende trigonometrische Funktionen:
Die Sinusfunktion

und Cosinusfunktion
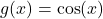 ,
,
die als Definitionsbereich die Menge  und als Wertebereich die Menge
und als Wertebereich die Menge ![Rendered by QuickLaTeX.com [-1, 1]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c7eedfc68f155bcb4cde8057b5e7740f_l3.png) haben, sowie
haben, sowie
die Tangensfunktion
 ,
,
die als Definitionsbereich die Menge  außer den Nullstellen der Cosinusfunktion hat und als Wertebereich die Menge
außer den Nullstellen der Cosinusfunktion hat und als Wertebereich die Menge  .
.
Trigonometrische Funktionen zeichnen
An dieser Stelle sind trigonometrische Funktionen noch sehr abstrakt. In diesem Abschnitt geben wir den einzelnen Funktionen eine anschauliche Gestalt. Hierzu nehmen wir eine kleine Wertetabelle auf, indem wir die  -Werte aus dem Intervall
-Werte aus dem Intervall ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) wählen und dazu die jeweiligen
wählen und dazu die jeweiligen  -Werte für jede trigonometrische Funktion ausrechnen. Die Tabelle mit den Werten kann dann folgendermaßen aussehen:
-Werte für jede trigonometrische Funktion ausrechnen. Die Tabelle mit den Werten kann dann folgendermaßen aussehen:
|
|
 |
 |
 |
 |
 |
 |
 |
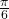 |
 |
 |
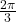 |
 |
|
 |
0 | -0,5 | -0,866 | -1 | -0,866 | -0,5 | 0 | 0,5 | 0,866 | 1 | 0,866 | 0,5 | 0 |
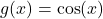 |
-1 | -0,866 | -0,5 | 0 | 0,5 | 0,866 | 1 | 0,866 | 0,5 | 0 | -0,5 | -0,866 | -1 |
 |
0 | 0,577 | 1,732 | n. d. | -1,732 | -0,577 | 0 | 0,577 | 1,732 | n. d. | -1,732 | -0,577 | 0 |
Hier steht „n. d.“ als Abkürzung für „nicht definiert“, denn bei diesen Werten für  würdest du durch Null dividieren. Wenn wir nun die Werte der Tabelle in ein Koordinatensystem eintragen und miteinander verbinden, erhalten wir ein Bild wie das Folgende. Beachte, dass sich die Tangensfunktion an den Stellen, an denen sie nicht definiert ist, einer senkrechten Asymptote nähert. Während die Sinus– und Cosinusfunktion nie größer als 1 beziehungsweise kleiner als -1 werden, erreicht die Tangensfunktion alle Werte entlang der y-Achse.
würdest du durch Null dividieren. Wenn wir nun die Werte der Tabelle in ein Koordinatensystem eintragen und miteinander verbinden, erhalten wir ein Bild wie das Folgende. Beachte, dass sich die Tangensfunktion an den Stellen, an denen sie nicht definiert ist, einer senkrechten Asymptote nähert. Während die Sinus– und Cosinusfunktion nie größer als 1 beziehungsweise kleiner als -1 werden, erreicht die Tangensfunktion alle Werte entlang der y-Achse.
Die Punkte stellen die Pärchen aus unserer Wertetabelle dar, die Kurven den tatsächlichen Funktionsgraphen der trigonometrischen Funktionen. Außerhalb der  -Werte unserer Wertetabelle haben wir die Funktionen aufgrund einer besonderen Eigenschaft weiterzeichnen können. Diese Eigenschaften werden wir im nächsten Abschnitt vorstellen. Die einzelnen Funktionsgraphen heißen auch Sinuskurve, Kosinuskurve und Tangenskurve.
-Werte unserer Wertetabelle haben wir die Funktionen aufgrund einer besonderen Eigenschaft weiterzeichnen können. Diese Eigenschaften werden wir im nächsten Abschnitt vorstellen. Die einzelnen Funktionsgraphen heißen auch Sinuskurve, Kosinuskurve und Tangenskurve.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Trigonometrische Funktionen Eigenschaften
Wir hatten erwähnt, dass erst bestimmte Eigenschaften Funktionen zu trigonometrische Funktionen machen. Welche Eigenschaften genau trigonometrische Funktionen besitzen, werden wir in diesem Abschnitt behandeln. Für die Cosinusfunktion und Tangensfunktion werden wir zusätzlich auf den Einfluss der verschiedenen Parameter eingehen. Für die Sinusfunktion haben wir dazu einen eigenen ausführlichen Beitrag für dich verfasst.
Trigonometrische Funktionen: Sinusfunktion
Wir beginnen mit der Sinusfunktion, die allgemein folgende Funktionsvorschrift besitzt
Allgemeine Form der Sinusfunktion
Die allgemeine Form ist gegeben durch
 ,
,
wobei  und
und  beliebige reelle Zahlen sind. Im Folgenden beschränken wir uns auf die einfache Funktion
beliebige reelle Zahlen sind. Im Folgenden beschränken wir uns auf die einfache Funktion  .
.
Definitionsbereich und Wertebereich
Für  ist
ist
der Definitionsbereich = die Menge  der reellen Zahlen und
der reellen Zahlen und
der Wertebereich = die Menge [-1,1] aller reellen Zahlen von -1 bis 1.
Amplitude, Periode und Symmetrie
Für sin(x) gilt
Periode von  beträgt
beträgt  und
und
Amplitude  .
.
Zusätzlich ist die Funktion punktsymmetrisch um den Ursprung. Es gilt also
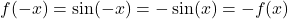 .
.
Nullstellen
Für die Nullstellen von  gilt
gilt

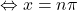 .
.
Hier ist  ein Element der Menge
ein Element der Menge  der ganzen Zahlen.
der ganzen Zahlen.
Extremwerte
Für die Extremwerte von  gilt
gilt
 und
und
 .
.
Manchmal findest du auch
 .
.
Trigonometrische Funktionen: Cosinusfunktion
Als nächstes beschäftigen wir uns mit der Cosinusfunktion, die folgende allgemeine Form besitzt
 ,
,
wobei  und
und  beliebige reelle Zahlen sind.
beliebige reelle Zahlen sind.
In den folgenden Unterabschnitten werden wir zunächst auf die unveränderte Cosinusfunktion eingehen, das heißt, wir setzen die Parameter auf  und
und  . Die Cosinusfunktion lautet dann
. Die Cosinusfunktion lautet dann
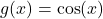 .
.
Weiter unten werden wir dir zeigen, welchen Einfluss die einzelnen Parameter auf den Verlauf des Funktionsgraphen der Cosinusfunktion haben.
Definitionsbereich und Wertebereich
Für die Cosinusfunktion cos(x) ist
der Definitionsbereich = die Menge  der reellen Zahlen und
der reellen Zahlen und
der Wertebereich = die Menge [-1,1] aller reellen Zahlen von -1 bis 1.
Amplitude und Periode
Kommen wir nun zur Eigenschaft, die es uns ermöglicht hat, den Funktionsgraphen der Cosinusfunktion ohne Kenntnis der Werte außerhalb unserer Wertetabelle zeichnen zu können. Diese Eigenschaft ist die Periodizität
der Cosinusfunktion. Das heißt, dass sich bei der Cosinusfunktion ein gewisses Muster wiederholt. Das Muster entspricht genau dem Verlauf der Cosinuskurve im Intervall von ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) . Du kannst also einfach das Muster in diesem Intervall nehmen, kopieren und dann so einfügen, dass der Graph verbunden bleibt. Und genau das haben wir bei der Konstruktion der Cosinuskurve aus der Wertetabelle ausgenutzt. Die „Breite“ dieses Musters heißt Periode und ist für den Fall der Cosinusfunktion
. Du kannst also einfach das Muster in diesem Intervall nehmen, kopieren und dann so einfügen, dass der Graph verbunden bleibt. Und genau das haben wir bei der Konstruktion der Cosinuskurve aus der Wertetabelle ausgenutzt. Die „Breite“ dieses Musters heißt Periode und ist für den Fall der Cosinusfunktion
Periode von 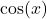 beträgt
beträgt  .
.
Du kannst an der Cosinuskurve erkennen, dass die Cosinusfunktion nie größer als +1 beziehungsweise kleiner als -1 wird. Diese „Barriere“ zwischen der die Werte der Cosinusfunktion auf- und abschwingen heißt Amplitude und hier gilt
Amplitude  .
.
Symmetrie
Ebenso kannst du aus der Cosinuskurve ableiten, dass die Funktion achsensymmetrisch um die y-Achse ist. Achsensymmetrie bedeutet, dass der Funktionsgraph links vom Ursprung durch Spiegelung des Funktionsgraphen rechts vom Ursprung an der y-Achse erhalten werden kann. Formal gilt also


Nullstellen
Der periodische Charakter der Cosinusfunktion erleichtert einige interessante Berechnungen. Da sich das Muster nach  wiederholt, reicht es beispielsweise für die Nullstellen der Cosinusfunktion (im Bild unten als grüne Punkte dargestellt) aus, sich nur auf das Intervall von
wiederholt, reicht es beispielsweise für die Nullstellen der Cosinusfunktion (im Bild unten als grüne Punkte dargestellt) aus, sich nur auf das Intervall von ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) zu konzentrieren. Alle anderen Nullstellen können wir aufgrund der Periodizität ableiten. An der Cosinuskurve erkennen wir, dass sich innerhalb von
zu konzentrieren. Alle anderen Nullstellen können wir aufgrund der Periodizität ableiten. An der Cosinuskurve erkennen wir, dass sich innerhalb von ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) die Nullstellen an den Stellen
die Nullstellen an den Stellen  und
und  befinden. Der Abstand zwischen zwei benachbarten Nullstellen ist also genau
befinden. Der Abstand zwischen zwei benachbarten Nullstellen ist also genau  . Die Periodizität der Cosinusfunktion erlaubt uns daher die allgemeine Feststellung, dass gilt
. Die Periodizität der Cosinusfunktion erlaubt uns daher die allgemeine Feststellung, dass gilt

 .
.
Hier ist  ein Element der Menge
ein Element der Menge  der ganzen Zahlen.
der ganzen Zahlen.
Extremwerte
Auch für die Extremwerte der Cosinusfunktion (im Bild unten als orangene Punkte dargestellt) reicht die Betrachtung im Intervall ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) . Anhand der Cosinuskurve können wir erkennen, dass die Funktion an den Stellen
. Anhand der Cosinuskurve können wir erkennen, dass die Funktion an den Stellen  und
und  ein Minimum und an der Stelle
ein Minimum und an der Stelle  ein Maximum besitzt. Der Abstand zwischen zwei benachbarten Maxima beziehungsweise Minima ist genau
ein Maximum besitzt. Der Abstand zwischen zwei benachbarten Maxima beziehungsweise Minima ist genau  . Der periodische Charakter der Cosinusfunktion lässt uns somit darauf schließen, dass die Minima und Maxima bei folgenden Werten liegen
. Der periodische Charakter der Cosinusfunktion lässt uns somit darauf schließen, dass die Minima und Maxima bei folgenden Werten liegen
 und
und
 .
.
Auch hier ist  eine ganze Zahl. Manchmal findest du auch
eine ganze Zahl. Manchmal findest du auch
 .
.
Der einzige Unterschied zwischen  und
und  liegt darin, dass du das Intervall
liegt darin, dass du das Intervall ![Rendered by QuickLaTeX.com [0, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c72ef3aaf0d173f4d649a858dd72f5f2_l3.png) an Stelle von
an Stelle von ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) betrachtest.
betrachtest.
Einfluss Parameter
Um den Einfluss der einzelnen Parameter auf den Verlauf des Kosinusfunktion zu erkennen, schauen wir uns ein konkretes Beispiel an. Dazu wählen wir die Parameter folgendermaßen
 und
und  .
.
Die Cosinusfunktion lautet dann
 .
.
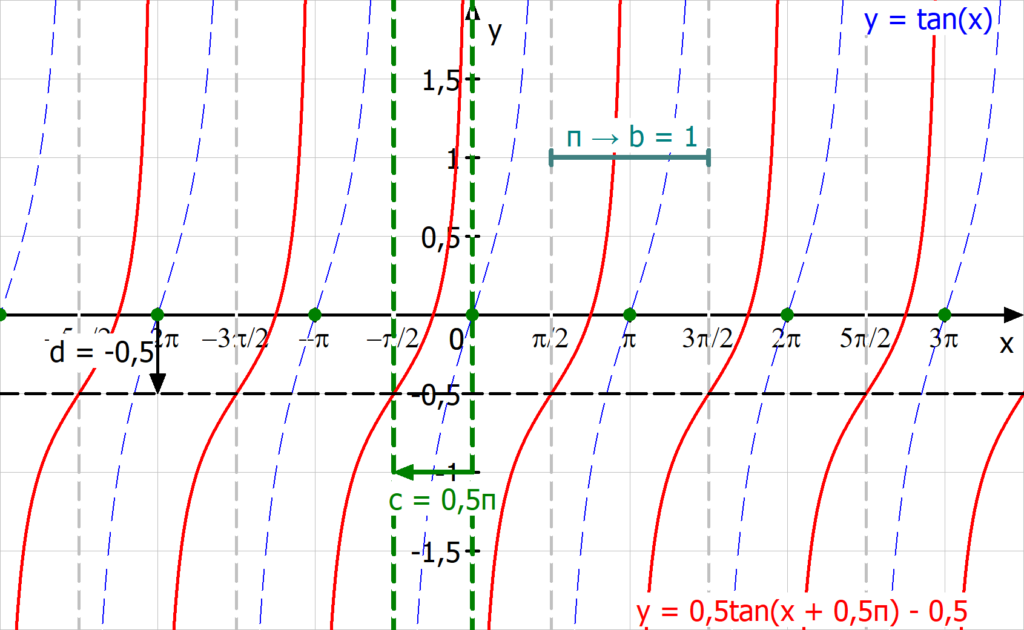
Der Funktionsgraph (rote durchgezogene Linie) sieht dann wie im folgenden Bild aus.
Die blaue gestrichelte Funktion stellt die normale Cosinusfunktion dar, also 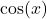 , und dient dazu, den Einfluss der Parameter zu veranschaulichen. Du erkennst, dass der Parameter d die Kurve nach oben verschiebt. Für negative Werte wird die Kurve nach unten verschoben. Der Parameter c verschiebt die Kurve nach rechts. Wäre c positiv, würde die Kurve nach links verschoben werden.
, und dient dazu, den Einfluss der Parameter zu veranschaulichen. Du erkennst, dass der Parameter d die Kurve nach oben verschiebt. Für negative Werte wird die Kurve nach unten verschoben. Der Parameter c verschiebt die Kurve nach rechts. Wäre c positiv, würde die Kurve nach links verschoben werden.
Weiterhin sollte dir auffallen, dass der Parameter a die Amplitude, um die die Cosinusfunktion um ihre Nullstellen schwingt, beeinflusst. Das heißt, dass die Parameter die Kurve entlang der y-Achse streckt, wenn  , beziehungsweise staucht, wenn
, beziehungsweise staucht, wenn  . Hier ist
. Hier ist  und die Cosinusfunktion schwingt nun um ihre verschobenen Nullstellen (durch die schwarz gestrichelte Linie dargestellt) mit der Amplitude 2.
und die Cosinusfunktion schwingt nun um ihre verschobenen Nullstellen (durch die schwarz gestrichelte Linie dargestellt) mit der Amplitude 2.
Der Parameter b streckt die Kurve entlang der x-Achse, wenn  , beziehungsweise staucht sie, wenn
, beziehungsweise staucht sie, wenn  . In diesem Beispiel ist
. In diesem Beispiel ist  , weshalb die Kurve entlang der x-Achse weder gestreckt noch gestaucht wurde. Dieser Parameter hat Einfluss darauf, wie schnell die Kurve auf- und abschwingt. Die Periode
, weshalb die Kurve entlang der x-Achse weder gestreckt noch gestaucht wurde. Dieser Parameter hat Einfluss darauf, wie schnell die Kurve auf- und abschwingt. Die Periode  , welche um b gestreckt oder gestaucht ist, kannst du folgendermaßen ausrechnen
, welche um b gestreckt oder gestaucht ist, kannst du folgendermaßen ausrechnen
 .
.
Trigonometrische Funktionen: Tangensfunktion
Zum Abschluss schauen wir uns die Eigenschaften der Tangensfunktion an, deren allgemeine Form folgendermaßen lautet
 ,
,
wobei  und
und  beliebige reelle Zahlen sind.
beliebige reelle Zahlen sind.
In den folgenden Unterabschnitten werden wir zunächst auf die unveränderte Tangensfunktion eingehen, das heißt, wir setzen die Parameter auf  und
und  . Die Tangensfunktion lautet dann
. Die Tangensfunktion lautet dann
 .
.
Am Ende dieses Abschnitts zeigen wir dir dann, welchen Einfluss die einzelnen Parameter auf diese trigonometrische Funktion haben.
Definitionsbereich und Wertebereich
Für die Tangensfunktion tan(x) ist
der Definitionsbereich = die Menge  der reellen Zahlen außer den Nullstellen der Cosinusfunktion
der reellen Zahlen außer den Nullstellen der Cosinusfunktion
der Wertebereich = die Menge  der reellen Zahlen.
der reellen Zahlen.
Amplitude, Periode und Symmetrie
Für  gilt
gilt
Periode von  beträgt
beträgt  .
.
Da die Tangensfunktion alle Werte entlang der y-Achse annehmen kann, kannst du keine Amplitude angeben.
Zusätzlich ist die Funktion punktsymmetrisch um den Ursprung. Punktsymmetrie bedeutet, dass der Funktionsgraph links vom Ursprung durch Spiegelung des Funktionsgraphen rechts vom Ursprung am Punkt (0,0) erhalten werden kann. Formal gilt also
 .
.
Das folgt direkt aus der Definition der Tangensfunktion als
 .
.
Da die Sinusfunktion punktsymmetrisch ist, gilt

und die Achsensymmetrie der Cosinusfunktion bedeutet
 .
.
Damit folgt
 ,
,
was gerade die formale Definition der Punktsymmetrie einer Funktion ist.
Nullstellen
Die Nullstellen der Tangensfunktion (im Bild unten als grüne Punkte dargestellt) sind gerade die Nullstellen der Sinusfunktion, da  im Zähler bei der Darstellung der Tangensfunktion als Bruch steht. Demnach gilt
im Zähler bei der Darstellung der Tangensfunktion als Bruch steht. Demnach gilt

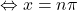 .
.
Hier ist  ein Element der Menge
ein Element der Menge  der ganzen Zahlen.
der ganzen Zahlen.
Polstellen
Die Tangensfunktion ist bei den Nullstellen der Cosinusfunktion nicht definiert, da 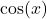 im Nenner steht. Du würdest also bei den Nullstellen der Cosinusfunktion durch Null dividieren. An diesen Stellen nähert sich die Tangensfunktion senkrechten Asymptoten
(im Bild unten grau gestrichelt dargestellt). Solche Stellen heißen Polstellen
. Es gilt also
im Nenner steht. Du würdest also bei den Nullstellen der Cosinusfunktion durch Null dividieren. An diesen Stellen nähert sich die Tangensfunktion senkrechten Asymptoten
(im Bild unten grau gestrichelt dargestellt). Solche Stellen heißen Polstellen
. Es gilt also
Polstellen der Tangensfunktion  = Nullstellen der Cosinusfunktion
= Nullstellen der Cosinusfunktion  .
.
Einfluss Parameter
Wie bei der Cosinsfunktion, schauen wir uns auch bei der Tangensfunktion ein konkretes Beispiel an, um den Einfluss der Parameter zu illustrieren. Dazu wählen wir die Parameter folgendermaßen
 und
und  .
.
Damit ergibt sich die Funktion

Der Funktionsgraph (rote durchgezogene Linie) sieht dann wie im folgenden Bild aus.
Die blaue gestrichelte Funktion stellt die normale Tangensfunktion dar, also  , und dient dazu, den Einfluss der Parameter zu veranschaulichen. Die Parameter haben auf den Verlauf der Tangensfunktion den gleichen Einfluss wie auf den Verlauf der Cosinusfunktion. Entsprechend verschiebt der Parameter d die Kurve entlang der y-Achse, der Parameter c verschiebt die Kurve entlang der x-Achse, der Parameter a streckt oder staucht die Kurve entlang der y-Achse und der Parameter b streckt oder staucht die Kurve entlang der x-Achse.
, und dient dazu, den Einfluss der Parameter zu veranschaulichen. Die Parameter haben auf den Verlauf der Tangensfunktion den gleichen Einfluss wie auf den Verlauf der Cosinusfunktion. Entsprechend verschiebt der Parameter d die Kurve entlang der y-Achse, der Parameter c verschiebt die Kurve entlang der x-Achse, der Parameter a streckt oder staucht die Kurve entlang der y-Achse und der Parameter b streckt oder staucht die Kurve entlang der x-Achse.
Den Parameter a kannst du leider nicht so einfach wie bei der Cosinusfunktion bestimmen. Was dieser aber macht, ist jeden Punkt entlang der blauen Kurve um den Fakor 0,5 zu stauchen. Für den Parameter d schaust du wieder, wohin die Nullstellen verschoben wurden. Ähnlich für den Parameter c, wobei hier die Nullstelle am Ursprung ausreicht.
Trigonometrische Funktionen ableiten
In diesem Abschnitt geben wir dir eine Zusammenfassung, wie du trigonometrische Funktionen ableiten kannst.
Sinusfunktion
Für die Funktion  gilt
gilt
 .
.
Cosinusfunktion
Für die Cosinusfunktion 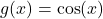 gilt
gilt
 .
.
Beachte, dass bei der hier ein Minuszeichen vorkommt.
Tangensfunktion
Für die Tangensfunktion  gilt
gilt
 .
.
Trigonometrische Funktionen Aufgaben
In diesem Abschnitt rechnen wir gemeinsam zwei Aufgaben für trigonometrische Funktionen. Bei der ersten Aufgabe wird es darum gehen, die Funktionsvorschrift einer verschobenen Cosinuskurve anhand des Graphen zu bestimmen. Bei der zweiten Aufgabe ist die Funktionsvorschrift einer Tangensfunktion gegeben und soll gezeichnet werden. Zudem soll die Tangensfunktion charakterisiert werden.
Lösung Aufgabe 1
Eine mögliche Methode ist sich eine unveränderte Cosinuskurve gedanklich im Koordinatensystem vorzustellen. Das könnte folgendermaßen aussehen.
Im ersten Schritt bestimmen wir den Parameter d. Dazu betrachten wir die Nullstellen der gedanklichen Kurve und ermitteln, wie weit diese nach unten verschoben wurde. In diesem Fall sind die Nullstellen um -2 verschoben und damit ist  . Als nächstes bestimmen wir die Amplitude. Die rote Kurve schwingt mit +1,5 beziehungsweise -1,5 um die verschobenen Nullstellen. Die Amplitude ist somit 1,5, also
. Als nächstes bestimmen wir die Amplitude. Die rote Kurve schwingt mit +1,5 beziehungsweise -1,5 um die verschobenen Nullstellen. Die Amplitude ist somit 1,5, also  . Die Breite eines Musters der roten Kurve ist genau
. Die Breite eines Musters der roten Kurve ist genau  . Daher wurde die Kurve in x-Richtung weder gestreckt noch gestaucht und somit ist
. Daher wurde die Kurve in x-Richtung weder gestreckt noch gestaucht und somit ist  . Für den Parameter c schauen wir uns das Maximum der originalen Kurve im Ursprung an. Wir erkennen, dass dieses um
. Für den Parameter c schauen wir uns das Maximum der originalen Kurve im Ursprung an. Wir erkennen, dass dieses um  nach rechts verschoben wurde, denn ab
nach rechts verschoben wurde, denn ab  beginnt die rote Kurve das gleiche Muster wie die originale Kurve zu haben. Damit ist
beginnt die rote Kurve das gleiche Muster wie die originale Kurve zu haben. Damit ist  .
.
Wir haben nun alle Parameterwerte gefunden und müssen diese nur noch in die allgemeine Form der Cosinusfunktion einsetzen. Wir erhalten dann für die gesuchte Funktionsvorschrift


Aufgabe 2: Tangenskurve zeichnen und charakterisieren
Zeichne die Funktionsvorschrift

und bestimme ihre Nullstellen und Polstellen im Intervall ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1954a1e860816a46e2b50f19b18c1824_l3.png) .
.
Trigonometrische Funktionen — häufigste Fragen
(ausklappen)
Trigonometrische Funktionen — häufigste Fragen
(ausklappen)-
Was macht eine Funktion zu einer trigonometrischen Funktion?Eine Funktion ist eine trigonometrische Funktion, wenn sie periodisch ist und zu den Winkelfunktionen wie Sinus, Cosinus oder Tangens gehört. Periodisch heißt, dass sich ihr Verlauf in festen Abständen wiederholt. Typische Grundformen sind
 ,
,  und
und  .
.
-
Wie zeichne ich Sinus, Cosinus und Tangens mit einer Wertetabelle?Sinus, Cosinus und Tangens zeichnest du, indem du
 -Werte (zum Beispiel aus
-Werte (zum Beispiel aus ![Rendered by QuickLaTeX.com [-\pi,\pi]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-85aeef0704e392045c401d8d5feeb72d_l3.png) ) auswählst, die Funktionswerte berechnest und die Punkte ins Koordinatensystem einträgst. Beispiel: Für
) auswählst, die Funktionswerte berechnest und die Punkte ins Koordinatensystem einträgst. Beispiel: Für  gilt
gilt  ,
,  und
und  ist nicht definiert, also wird dort kein Punkt gesetzt.
ist nicht definiert, also wird dort kein Punkt gesetzt.
-
Warum ist die Tangensfunktion an manchen Stellen nicht definiert?Die Tangensfunktion ist an den Nullstellen der Cosinusfunktion nicht definiert, weil
 ist und dann durch 0 geteilt würde. Diese Stellen heißen Polstellen und der Graph nähert sich dort senkrechten Asymptoten. Beispiel: Bei
ist und dann durch 0 geteilt würde. Diese Stellen heißen Polstellen und der Graph nähert sich dort senkrechten Asymptoten. Beispiel: Bei  ist
ist  , daher ist
, daher ist  nicht definiert.
nicht definiert.
-
Welche Symmetrie hat die Sinusfunktion und wie erkenne ich sie?Die Sinusfunktion ist punktsymmetrisch zum Ursprung, das heißt es gilt
 . Erkennen lässt sich das daran, dass zu jedem Punkt
. Erkennen lässt sich das daran, dass zu jedem Punkt  auch der Punkt
auch der Punkt  auf dem Graphen liegt. Beispiel: Aus
auf dem Graphen liegt. Beispiel: Aus  folgt
folgt  .
.
-
Wie verändern a, b, c und d den Graphen von Cosinus?In
 verschiebt
verschiebt  den Graphen nach oben oder unten und
den Graphen nach oben oder unten und  verschiebt ihn nach rechts oder links. Der Parameter
verschiebt ihn nach rechts oder links. Der Parameter  streckt oder staucht in y-Richtung (Amplitude) und
streckt oder staucht in y-Richtung (Amplitude) und  streckt oder staucht in x-Richtung; die Periode ist
streckt oder staucht in x-Richtung; die Periode ist  .
.
Lösung Aufgabe 2
Wir erkennen, dass die originale Tangenskurve um  nach links verschoben wurde. Entlang der y-Achse wurde sie nicht verschoben. Die Kurve geht also durch den Punkt (
nach links verschoben wurde. Entlang der y-Achse wurde sie nicht verschoben. Die Kurve geht also durch den Punkt ( , 0). Die Amplitude wurde um den Faktor 0,2 gestaucht. Da hier
, 0). Die Amplitude wurde um den Faktor 0,2 gestaucht. Da hier  ist, ist die Periode unverändert gleich
ist, ist die Periode unverändert gleich  . Wir beginnen daher im Punkt (
. Wir beginnen daher im Punkt ( , 0) die Tangenskurve zu zeichnen, indem wir in den Taschenrechner ein paar Werte für
, 0) die Tangenskurve zu zeichnen, indem wir in den Taschenrechner ein paar Werte für  aus dem Intervall
aus dem Intervall  einsetzen. Beachte, dass die Polstellen, an denen die unveränderte Tangensfunktion nicht definiert ist, ebenfalls um
einsetzen. Beachte, dass die Polstellen, an denen die unveränderte Tangensfunktion nicht definiert ist, ebenfalls um  nach links verschoben wurden.
nach links verschoben wurden.
Wir haben in diesem Bild bereits die Polstellen mit  ,
,  und
und  , sowie die Nullstellen mit
, sowie die Nullstellen mit  und
und  gekennzeichnet. Außerdem haben wir durch die blau gestrichelten Linien die senkrechten Asymptoten dargestellt. Aus diesem Bild erkennen wir
gekennzeichnet. Außerdem haben wir durch die blau gestrichelten Linien die senkrechten Asymptoten dargestellt. Aus diesem Bild erkennen wir
Polstellen bei  ,
,  und
und  sowie
sowie
Nullstellen bei  und
und  .
.