Hesse Matrix
Die Hesse Matrix stellt für mehrdimensionale reellwertige Funktionen das Analogon zur 2. Ableitung dar. Um die Hesse Matrix berechnen zu können, werden sämtliche zweiten partiellen Ableitungen der Funktion benötigt. Es können über die Definitheit der Hesse Matrix, die Extremstellen einer Funktion aufgrund ihres Krümmungsverhaltens klassifiziert werden.
Willst du das alles in weniger als 5 Minuten erklärt bekommen? Dann sieh dir unser Video dazu an!
Inhaltsübersicht
Definition: Hesse Matrix
Sei  offen und die Funktion
offen und die Funktion  sei zweimal stetig differenzierbar
. Dann ist die Hesse Matrix (auch Hessematrix oder Hessesche Matrix) von
sei zweimal stetig differenzierbar
. Dann ist die Hesse Matrix (auch Hessematrix oder Hessesche Matrix) von  im Punkt
im Punkt  die folgende n×n-Matrix:
die folgende n×n-Matrix:


Häufig wird die Hesse Matrix auch mit  abgekürzt.
abgekürzt.
Symmetrische Hesse Matrix
Da die Funktion zweimal stetig differenzierbar ist, gilt für die partiellen Ableitungen nach dem Satz von Schwarz:
 bzw.
bzw. 
Das bedeutet, dass die Hessesche Matrix eine symmetrische Matrix ist.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Gradient und Hesse Matrix
Der Gradient
der betrachteten Funktion  sieht an der Stelle
sieht an der Stelle  bekanntlich folgendermaßen aus:
bekanntlich folgendermaßen aus:
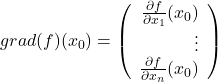
Die Totale Ableitung bzw. Jacobi-Matrix
des Gradienten  an der Stelle
an der Stelle  ergibt dann gerade die transponierte Hesse Matrix:
ergibt dann gerade die transponierte Hesse Matrix:
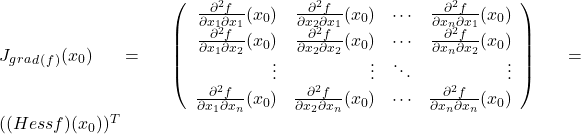
Da die zweiten partiellen Ableitungen der Funktion f stetig sind, ist die Hessesche Matrix wie bereits erwähnt symmetrisch und somit entspricht die Jacobi-Matrix des Gradienten genau der Hesse Matrix selbst.
Hesse Matrix berechnen
Zur Berechnung der Hesse Matrix müssen also nur alle möglichen partiellen Ableitungen 2. Ordnung bestimmt werden und in richtiger Reihenfolge in einer Matrix angeordnet werden. Um die Übersicht nicht zu verlieren kann hierfür zunächst der Gradient berechnet und notiert werden. Anschließend muss nur noch die Jacobi-Matrix des Gradienten berechnet werden und man erhält die Hesse Matrix.
Die Berechnung der Hesse Matrix soll anhand zweier Beispiele vorgeführt werden.
Hesse Matrix Beispiel 1
Im ersten Beispiel soll die Hessesche Matrix der Funktion  an der Stelle
an der Stelle  berechnet werden. Dazu wird wie bereits beschrieben zunächst der Gradient dieser Funktion bestimmt. Dieser lautet:
berechnet werden. Dazu wird wie bereits beschrieben zunächst der Gradient dieser Funktion bestimmt. Dieser lautet:

Nun ist die Hesse Matrix gerade die Jacobi-Matrix des Gradienten. Um diese zu bestimmen, werden die partiellen Ableitungen nach x und y der beiden Komponenten  und
und  des Gradienten ermittelt und in richtiger Reihenfolge angeordnet:
des Gradienten ermittelt und in richtiger Reihenfolge angeordnet:


Hier ist noch einmal gut zu erkennen, dass die Hessesche Matrix tatsächlich symmetrisch ist. Diese Tatsache kann als Kontrolle dienen und sollte immer überprüft werden.
Hesse Matrix Beispiel 2
Nun soll die Hesse Matrix der Funktion  an der Stelle
an der Stelle  berechnet werden. Da die Funktion von drei Variablen abhängt, wird die zugehörige Hesse Matrix eine 3×3-Matrix sein. Um sie an der Stelle
berechnet werden. Da die Funktion von drei Variablen abhängt, wird die zugehörige Hesse Matrix eine 3×3-Matrix sein. Um sie an der Stelle  zu bestimmen, wird sie zunächst für die allgemeine Stelle
zu bestimmen, wird sie zunächst für die allgemeine Stelle  berechnet und zum Schluss werden die entsprechenden Werte in das Ergebnis eingesetzt. Der Gradient von f an der Stelle
berechnet und zum Schluss werden die entsprechenden Werte in das Ergebnis eingesetzt. Der Gradient von f an der Stelle  lautet:
lautet:

Die Hessesche Matrix an der Stelle  ist die Jacobi-Matrix dieses Gradienten:
ist die Jacobi-Matrix dieses Gradienten:

Sie lautet demnach:

Auch hier lässt sich mit einem Blick überprüfen, dass die Hesse Matrix symmetrisch ist. Da die Hesse Matrix an der Stelle  gesucht wird, müssen diese Werte noch für (x,y,z) eingesetzt werden. Das gesuchte Ergebnis lautet somit:
gesucht wird, müssen diese Werte noch für (x,y,z) eingesetzt werden. Das gesuchte Ergebnis lautet somit:

Bedeutung der Hesse Matrix
Der Hesse Matrix kommt für mehrdimensionale reellwertige Funktionen eine ähnliche Bedeutung zu wie der 2. Ableitung für reellwertige Funktionen einer Variablen. Das bedeutet, dass mithilfe der Hesse Matrix Aussagen über das Krümmungsverhalten einer Funktion getroffen werden können.
Hesse Matrix Definitheit und Krümmungsverhalten
Es soll die offene Teilmenge  und eine zweimal stetig differenzierbare Funktion
und eine zweimal stetig differenzierbare Funktion  betrachtet werden. Für das Krümmungsverhalten auf der konvexen Menge
betrachtet werden. Für das Krümmungsverhalten auf der konvexen Menge  gelten folgende Zusammenhänge:
gelten folgende Zusammenhänge:
- f ist auf D genau dann konvex, wenn die Hesse Matrix auf ganz D positiv semidefinit ist.
- f ist auf D genau dann strikt konvex, wenn die Hesse Matrix auf ganz D positiv definit ist.
- f ist auf D genau dann konkav, wenn die Hesse Matrix auf ganz D negativ semidefinit ist.
- f ist auf D genau dann strikt konkav, wenn die Hesse Matrix auf ganz D negativ definit ist.
Die Definitheit einer Matrix A kann mithilfe ihrer Eigenwerte überprüft werden. Es gelten hierfür folgende Zusammenhänge:
- A ist genau dann positiv (negativ) definit, wenn alle Eigenwerte von A positiv (negativ) sind.
- A ist genau dann positiv (negativ) semidefinit, wenn alle Eigenwerte ≥0 (≤0) sind.
- A ist genau dann indefinit, wenn A mindestens einen positiven und einen negativen Eigenwert besitzt.
Für größere Matrizen ist es häufig kompliziert sämtliche Eigenwerte zu bestimmen. In diesem Fall bietet sich das Kriterium der führenden Hauptminoren an. Die führenden Hauptminoren  einer n×n-Matrix sind dabei die Determinanten der Untermatrizen, die dadurch entstehen, dass man sukzessive die letzte Zeile und Spalte der Matrix streicht. Beispielsweise sind die führenden Hauptminoren der Matrix
einer n×n-Matrix sind dabei die Determinanten der Untermatrizen, die dadurch entstehen, dass man sukzessive die letzte Zeile und Spalte der Matrix streicht. Beispielsweise sind die führenden Hauptminoren der Matrix  die Determinanten der drei Untermatrizen
die Determinanten der drei Untermatrizen ,
,  und
und  :
:
 ,
,  ,
, 
Das Hauptminoren-Kriterium lautet:
- A ist genau dann positiv definit, wenn alle führenden Hauptminoren von A positiv sind.
- A ist genau dann negativ definit, wenn alle ungeraden führenden Hauptminoren von A negativ und alle geraden führenden Hauptminoren von A positiv sind.
Anwendungen der Hesse Matrix
Bekanntlich tritt die 2. Ableitung in der Taylorentwicklung einer Funktion auf und außerdem können mit ihrer Hilfe die Typen der Extremstellen einer Funktion ermittelt werden. In diesen beiden Fällen kommt somit auch die Hessesche Matrix als Analogon der 2. Ableitung zum Einsatz.
Taylorentwicklung
Für die zweimal stetig differenzierbare Funktion  lautet die Taylorentwicklung
bis zur zweiten Ordnung um den Punkt
lautet die Taylorentwicklung
bis zur zweiten Ordnung um den Punkt  :
:

Für reellwertige Funktionen einer Variablen ist dies genau das herkömmliche Taylorpolynom 2. Grades:

Mit der Hesse Matrix Extremstellen klassifizieren
Mithilfe der Kenntnis über das Krümmungsverhalten einer Funktion, die man aus der Hesse Matrix gewinnen kann, lassen sich die Extremstellen dieser Funktion charakterisieren. Dazu müssen allerdings zunächst die kritischen Punkte der Funktion ermittelt werden. Das sind genau diejenigen Punkte, an denen der Gradient der Funktion verschwindet:
 ist ein kritischer Punkt
ist ein kritischer Punkt 
Ob ein kritischer Punkt ein lokales Maximum oder Minimum darstellt, lässt sich häufig mithilfe der Definitheit der Hesse Matrix ermitteln.
- Ist
 ein kritischer Punkt und ist die Hesse Matrix dort positiv definit, dann ist in
ein kritischer Punkt und ist die Hesse Matrix dort positiv definit, dann ist in  ein lokales Minimum der Funktion.
ein lokales Minimum der Funktion. - Ist
 ein kritischer Punkt und ist die Hesse Matrix dort negativ definit, dann ist in
ein kritischer Punkt und ist die Hesse Matrix dort negativ definit, dann ist in  ein lokales Maximum der Funktion.
ein lokales Maximum der Funktion. - Ist
 ein kritischer Punkt und ist die Hesse Matrix dort indefinit, dann ist in
ein kritischer Punkt und ist die Hesse Matrix dort indefinit, dann ist in  ein Sattelpunkt.
ein Sattelpunkt.
Ist ein kritischer Punkt und ist die Hesse Matrix dort semidefinit, so kann auf diese Art und Weise der Charakter der Extremstelle nicht ermittelt werden.
ein kritischer Punkt und ist die Hesse Matrix dort semidefinit, so kann auf diese Art und Weise der Charakter der Extremstelle nicht ermittelt werden.
Anhand zweier Beispiele soll im Folgenden das schrittweise Vorgehen zur Bestimmung der Extrema illustriert werden.
Extremstellen und Hesse Matrix Beispiel 1
Im ersten Beispiel soll die Funktion  auf Extremstellen untersucht werden.
auf Extremstellen untersucht werden.
Dazu müssen zunächst die kritischen Punkte dieser Funktion ermittelt werden. Diese sind gerade die Nullstellen des Gradienten, welcher wie folgt aussieht:

Die Nullstellen dieses Gradienten sind gerade die Lösungen des folgenden Gleichungssystems:
Dieses wird lediglich durch den Punkt  gelöst, welcher somit der einzige kritische Punkt der Funktion f ist. An diesem Punkt muss also die Hesse Matrix der Funktion auf Definitheit überprüft werden, um die Art der Extremstelle ermitteln zu können. Hierfür muss die Hessesche Matrix zunächst einmal berechnet werden. Sie lautet:
gelöst, welcher somit der einzige kritische Punkt der Funktion f ist. An diesem Punkt muss also die Hesse Matrix der Funktion auf Definitheit überprüft werden, um die Art der Extremstelle ermitteln zu können. Hierfür muss die Hessesche Matrix zunächst einmal berechnet werden. Sie lautet:


Das bedeutet, dass die Hesse Matrix unabhängig von den beiden Variablen ist und an jeder beliebigen Stelle  die Form
die Form  besitzt. Das gilt somit auch für die einzige kritische Stelle
besitzt. Das gilt somit auch für die einzige kritische Stelle  der Funktion:
der Funktion:
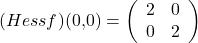
Diese Matrix muss nun auf Definitheit überprüft werden. Dazu können die Eigenwerte  und
und  der Matrix bestimmt werden. Diese sind gerade die Nullstellen des charakteristischen Polynoms
der Matrix bestimmt werden. Diese sind gerade die Nullstellen des charakteristischen Polynoms  . Es gilt also
. Es gilt also  , was bedeutet, dass die Hesse Matrix an der kritischen Stelle
, was bedeutet, dass die Hesse Matrix an der kritischen Stelle  positiv definit ist und demzufolge dort ein Minimum besitzt.
positiv definit ist und demzufolge dort ein Minimum besitzt.
Extremstellen und Hesse Matrix Beispiel 2
Nun sollen die Extrema der Funktion  bestimmt werden.
bestimmt werden.
Zunächst werden wieder die kritischen Stellen der Funktion mithilfe des Gradienten bestimmt:

Dessen Nullstellen sind die Lösungen des folgenden Gleichungssystems:
Die Punkte, die dieses Gleichungssystem erfüllen sind: 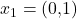 und
und  . Das sind also die kritischen Stellen, für welche die Definitheit der Hesse Matrix untersucht werden muss. Dazu wird im ersten Schritt die Hesse Matrix an der Stelle
. Das sind also die kritischen Stellen, für welche die Definitheit der Hesse Matrix untersucht werden muss. Dazu wird im ersten Schritt die Hesse Matrix an der Stelle  berechnet:
berechnet:


Für die Hessesche Matrix an den kritischen Punkten 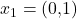 und
und  gilt also:
gilt also:


Nun gilt es diese Matrizen auf Definitheit zu untersuchen. Dazu werden die Eigenwerte als Nullstellen der charakteristischen Polynome  bestimmt. Das bedeutet, dass beide Matrizen die Eigenwerte
bestimmt. Das bedeutet, dass beide Matrizen die Eigenwerte  und
und  besitzen. Das heißt nichts anderes, als dass die Hesse Matrix der Funktion an beiden kritischen Stellen indefinit ist und somit dort einen Sattelpunkt besitzt.
besitzen. Das heißt nichts anderes, als dass die Hesse Matrix der Funktion an beiden kritischen Stellen indefinit ist und somit dort einen Sattelpunkt besitzt.






