Newton Verfahren
In diesem Artikel erklären wir dir anhand einiger Beispiele, wozu du das Newton Verfahren verwendest und wie du bei der Durchführung vorgehen kannst. In unserem Video dazu haben wir das Wichtigste kurz und kompakt zusammengefasst.
Inhaltsübersicht
Newtonverfahren einfach erklärt
Mit dem Newton-Verfahren (oder auch Newton Raphson Verfahren) kann man die Nullstellen einer Funktion näherungsweise bestimmen. Beim Newton Verfahren wird ein Anfangswert in eine Formel und anschließend das erhaltene Ergebnis erneut in die Formel eingesetzt. Führt man das weiter fort, so erhält man im Idealfall ein immer besseres Ergebnis für eine Nullstelle der Funktion. Die Berechnung der Nullstelle erfolgt also näherungsweise. Ein solches Verfahren nennt man Iterationsverfahren.
Newton Verfahren Formel
Die Formel für das Newton-Verfahren sieht folgendermaßen aus:

Die Formel wird Iterationsformel genannt.  ist der neue Wert, der berechnet wird und
ist der neue Wert, der berechnet wird und  ist der Wert, der im vorherigen Schritt ermittelt wurde.
ist der Wert, der im vorherigen Schritt ermittelt wurde.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Newton Verfahren Beispiel
Für die Funktion  lautet die Iterationsformel folgendermaßen:
lautet die Iterationsformel folgendermaßen:

Hierfür muss nur die Ableitung
 der Funktion bestimmt werden und in die allgemeine Formel eingesetzt werden.
der Funktion bestimmt werden und in die allgemeine Formel eingesetzt werden.
Newton Verfahren Aufgaben
Nun wollen wir einmal konkret das Newtonverfahren an folgender Beispielfunktion durchführen:

Zunächst bestimmen wir die Ableitung der Funktion.

Nun ersetzen wir in der Funktion und der Ableitung das  durch
durch  .
.


Beides wird jetzt in die Iterationsformel eingesetzt.

In diese Formel können wir nun einen Startwert für  einsetzen (den wir
einsetzen (den wir  nennen) und erhalten als Ergebnis einen neuen Wert. Diesen setzen wir dann wieder in die Formel ein und führen das ganze so weiter. Irgendwann erhalten wir dann einen Wert, der einer Nullstelle der Funktion sehr nahe kommt. Allerdings sollte man am Anfang darauf achten, welchen Wert
nennen) und erhalten als Ergebnis einen neuen Wert. Diesen setzen wir dann wieder in die Formel ein und führen das ganze so weiter. Irgendwann erhalten wir dann einen Wert, der einer Nullstelle der Funktion sehr nahe kommt. Allerdings sollte man am Anfang darauf achten, welchen Wert  man als erstes in die Formel einsetzt. Setzt man nämlich einen ungünstigen Wert ein, kann es passieren, dass das Verfahren nicht funktioniert und man sich nie einer Nullstelle der Funktion nähert.
man als erstes in die Formel einsetzt. Setzt man nämlich einen ungünstigen Wert ein, kann es passieren, dass das Verfahren nicht funktioniert und man sich nie einer Nullstelle der Funktion nähert.
Startwert bestimmen
In Aufgaben wird häufig ein Intervall angegeben, auf dem man sich einer Nullstelle mit dem Newton Verfahren nähern soll. Dann kann man als Startwert die Mitte dieses Intervalls wählen.
Wird kein solches Intervall angegeben, kann man eine Wertetabelle anlegen und nach einem Vorzeichenwechsel Ausschau halten. Den Startwert sollte man dann in dem Intervall wählen, in dem der Vorzeichenwechsel stattfindet.
Hier ist eine Wertetabelle für unsere Funktion  dargestellt.
dargestellt.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | -193 | -64 | -9 | 2 | -1 | 12 | 71 | 206 | 447 |
Auf dem betrachteten Bereich gibt es Vorzeichenwechsel auf den folgenden Intervallen:
![Rendered by QuickLaTeX.com [-2; -1] ; [-1; 0] ; [0; 1]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ab7642fc6b44a3315541b6795725ed73_l3.png)
Wir wollen in diesem Beispiel die Nullstelle auf dem Intervall ![Rendered by QuickLaTeX.com [0; 1]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9664472daec3488317d11d3867cc615c_l3.png) nähern und wählen dementsprechend als Startwert den Wert
nähern und wählen dementsprechend als Startwert den Wert
 .
.
Diesen setzen wir nun in die Iterationsvorschrift ein und berechnen den Wert  :
:

Wir runden in unserem Beispiel auf fünf Nachkommastellen und erhalten den folgenden Wert:

Diesen können wir nun wieder in die Iterationsformel einsetzen und erhalten  :
:


Auf dieselbe Art berechnet sich der nächste Wert  :
:


Und man erkennt schon, dass sich die zweite Nachkommastelle bereits nicht mehr verändert hat. Wir berechnen den Wert  :
:


Bei diesem Schritt sind schon die ersten vier Nachkommastellen gleichgeblieben. Der Wert  lautet:
lautet:


In diesem Schritt hat sich keine der fünf betrachteten Nachkommastellen mehr verändert. Wir haben uns also mit einer Genauigkeit von fünf Nachkommastellen einer Nullstelle der Funktion genähert. Zur Sicherheit kann das Ergebnis noch in die Funktion eingesetzt werden und überprüft werden, ob es sich tatsächlich um eine Nullstelle handelt:

Newton Verfahren Herleitung
Zur Herleitung der Iterationsvorschrift wollen wir uns die Idee des Newtonverfahrens ansehen. Das Ganze werden wir uns grafisch überlegen. Wenn wir eine Stelle  kennen, an der die Funktion
kennen, an der die Funktion  einen kleinen Wert annimmt, legen wir an dieser Stelle eine Tangente an den Funktionsgraphen von
einen kleinen Wert annimmt, legen wir an dieser Stelle eine Tangente an den Funktionsgraphen von  . Wir linearisieren
also die Funktion um die betrachtete Stelle. Das bedeutet, dass wir eine lineare Näherungsfunktion finden. Die Nullstelle der Tangenten ist dann sogleich unser erster Näherungswert
. Wir linearisieren
also die Funktion um die betrachtete Stelle. Das bedeutet, dass wir eine lineare Näherungsfunktion finden. Die Nullstelle der Tangenten ist dann sogleich unser erster Näherungswert  für die Nullstelle von
für die Nullstelle von  .
.
Um den nächsten Näherungswert  zu erhalten, bilden wir nun die Tangente an den Graphen von
zu erhalten, bilden wir nun die Tangente an den Graphen von  an der Stelle
an der Stelle  und betrachten wieder deren Nullstelle. So führen wir das Verfahren immer weiter, bis wir eine ausreichende Genauigkeit der Näherung erhalten haben.
und betrachten wieder deren Nullstelle. So führen wir das Verfahren immer weiter, bis wir eine ausreichende Genauigkeit der Näherung erhalten haben.
Nun wollen wir zeigen, dass dieses Vorgehen zu der oben beschriebenen Iterationsformel führt. Die Tangente an den Graphen von  an der Stelle
an der Stelle  besitzt die Steigung
besitzt die Steigung 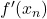 und die Tangentengleichung lautet:
und die Tangentengleichung lautet:

Nun wollen wir die Nullstelle dieser Tangente bestimmen, um den Wert  zu erhalten. Es muss also gelten:
zu erhalten. Es muss also gelten:


Diese Gleichung lösen wir nun nach  auf und erhalten unsere Iterationsvorschrift:
auf und erhalten unsere Iterationsvorschrift:

Das Ziel des Newton Verfahrens ist die Annäherung an Nullstellen: Indem du die Ergebnisse immer wieder in die Newton Formel einsetzt, näherst du die Nachkommastellen der Nullstelle an. Diese Art von Verfahren nennst du auch Iterationsverfahren.
Konvergenz Newton Verfahren
Ob das Newtonverfahren immer zum Ziel führt hängt wie schon erwähnt von der Wahl des Startwertes  ab. Die Folge der berechneten Werte
ab. Die Folge der berechneten Werte  konvergiert nur dann mit Sicherheit, wenn der Startpunkt
konvergiert nur dann mit Sicherheit, wenn der Startpunkt  schon ausreichend nahe an der gesuchten Nullstelle liegt. Die Newtoniteration stellt also ein lokal konvergentes Verfahren dar. Der Bereich um die Nullstelle, innerhalb dessen man den Startwert wählen darf, sodass das Verfahren garantiert konvergiert, wird Konvergenzbereich genannt.
schon ausreichend nahe an der gesuchten Nullstelle liegt. Die Newtoniteration stellt also ein lokal konvergentes Verfahren dar. Der Bereich um die Nullstelle, innerhalb dessen man den Startwert wählen darf, sodass das Verfahren garantiert konvergiert, wird Konvergenzbereich genannt.
Liegt der Startwert  außerhalb des Konvergenzbereichs, so kann die Folge divergieren, oszillieren oder auch gegen eine andere Nullstelle der Funktion konvergieren.
außerhalb des Konvergenzbereichs, so kann die Folge divergieren, oszillieren oder auch gegen eine andere Nullstelle der Funktion konvergieren.
Gedämpftes Newtonverfahren
Der Konvergenzbereich kann vergrößert werden, indem die Formel des Newton Verfahrens ein wenig angepasst wird:

Der Dämpfungsparameter  wird dabei im Intervall
wird dabei im Intervall ![Rendered by QuickLaTeX.com (0; 1]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4be02f3ab0ca93c4a8b652a24f4045d8_l3.png) gewählt. Für die ersten Folgeglieder kann er klein gewählt werden, um die Konvergenz zu sichern. Für höhere Folgeglieder sollte er größer werden um eine schnellere Konvergenz zu erhalten.
gewählt. Für die ersten Folgeglieder kann er klein gewählt werden, um die Konvergenz zu sichern. Für höhere Folgeglieder sollte er größer werden um eine schnellere Konvergenz zu erhalten.
Newtonverfahren mehrdimensional
Auch für mehrdimensionale Funktionen  können mithilfe des Newton-Verfahrens Nullstellen bestimmt werden. Die Linearisierung, also die Taylorentwicklung
1. Ordnung im Punkt
können mithilfe des Newton-Verfahrens Nullstellen bestimmt werden. Die Linearisierung, also die Taylorentwicklung
1. Ordnung im Punkt  lautet dann:
lautet dann:

Hierbei ist  die Jacobi-Matrix
der Funktion
die Jacobi-Matrix
der Funktion  an der Stelle
an der Stelle  . Sie enthält sämtliche partiellen Ableitungen
der Funktion
. Sie enthält sämtliche partiellen Ableitungen
der Funktion  . Die Suche nach der Nullstelle
. Die Suche nach der Nullstelle  dieser Linearisierung führt zur Newtoniteration:
dieser Linearisierung führt zur Newtoniteration:


In Kombination mit der gaußschen Fehlerquadratmethode ergibt sich dann das Gauß Newton Verfahren.
