Video

Quiz

Hier geht's zum Video „Polarkoordinaten“

Hier geht's zum Video „Orthogonale Projektion“

Hier geht's zum Video „Jacobi-Matrix“

Zylinderkoordinaten

Wichtige Inhalte in diesem Video

Zylinderkoordinatendarstellung

Zylinderkoordinaten in kartesische Koordinaten umrechnen

In diesem Artikel werden die Zylinderkoordinaten eingeführt. Außerdem wird deren Umrechnung mit den kartesischen Koordinaten erläutert. Darüber hinaus werden auch die Volumen-, Flächen– und Linienelemente sowie die Einheitsbasisvektoren und der Nabla– und Laplace-Operator bestimmt.

Um dir die Thematik der Zylinderkoordinaten audiovisuell näher zubringen, haben wir für dich auch ein anschauliches Video erstellt!

Inhaltsübersicht

Zylinderkoordinaten Definition

Merke

In Zylinderkoordinaten wird ein Punkt im Dreidimensionalen durch die Angabe seines Abstands

zu einer vorgegebenen Achse, eines Winkels $\phi$ und einer Höhe

beschrieben.

Im Wesentlichen entsprechen sie den ebenen Polarkoordinaten, welche um die Höhe erweitert wurden.

Zylinderkoordinatensystem

Das Zylinderkoordinatensystem zeichnet sich zum einen durch eine gerichtete Gerade aus, welche auch als zylindrische oder longitudale Achse bezeichnet wird. In der Regel wird hierfür die -Achse des kartesischen Koordinatensystems gewählt. Außerdem gehört eine Halbgerade, die senkrecht auf der zylindrischen Achse steht, zum Zylinderkoordinatensystem. Diese bezeichnet man als Polachse und wählt hierfür meist die positive -Achse des kartesischen Koordinatensystems. Dort, wo sie auf die zylindrische Achse trifft, liegt der Ursprung des Koordinatensystems. Orthogonal zur zylindrischen Achse und durch den Ursprung läuft die sogenannte Bezugsebene.

Zylinderkoordinatendarstellung

im Videozur Stelle im Video springen

Projiziert man einen Punkt im Raum orthogonal auf die Bezugsebene, so kann der Punkt der orthogonalen Projektion in der Bezugsebene durch die Polarkoordinaten $(r,\phi)$ beschrieben werden. Hierbei stellt den Abstand des projizierten Punktes zum Ursprung dar und $\phi$ beschreibt den Winkel zwischen der Polachse und der Verbindungsstrecke vom Ursprung zum projizierten Punkt. Um nicht die Projektion zu beschreiben, sondern den Punkt selbst, werden die beiden Koordinaten um die Höhe ergänzt. Sie gibt den Abstand des Punktes zur Bezugsebene an. Liegt der Punkt oberhalb der Ebene, bekommt die Koordinate ein positives Vorzeichen, wohingegen es negativ ist, falls der Punkt unterhalb der Bezugsebene liegt. Das Zahlenpaar $(r,\phi, z)$ nennt man Zylinderkoordinaten des Punktes .

Zylinderkoordinaten umrechnen

Von großer Bedeutung ist die Umrechnung der Zylinderkoordinaten mit den kartesischen Koordinaten. Hierfür ist es am einfachsten, das Zylinderkoordinatensystem so zu wählen, dass die zylindrische Achse auf die -Achse und die Polachse auf die positive -Achse des kartesische Systems fällt.

Zylinderkoordinaten in kartesische Koordinaten umrechnen

im Videozur Stelle im Video springen

Für die Umrechnung in kartesische Koordinaten ergeben sich nach geometrischen Überlegungen folgende Formeln:

$x=r\cdot \cos{\phi}$

$y=r\cdot \sin{\phi}$

z=z

Die Umrechnung entspricht für die – und -Koordinate derjenigen der Polarkoordinaten.

Kartesische Koordinaten in Zylinderkoordinaten umrechnen

Auch die umgekehrte Umrechnung erfolgt für die ersten beiden Koordinaten wie bei den Polarkoordinaten, während die -Koordinate unverändert bleibt:

$r=\sqrt{x^2+y^2}$

$\phi=\arctan{\frac{y}{x}}$

z=z

Hierbei ist zu beachten, dass die Umrechnung für die Koordinate $\phi$ in dieser Form nur für den Fall gilt, dass und größer null sind. Eine genaue Fallunterscheidung findest du in unserem Artikel zu den Polarkoordinaten .

Transformation von Differentialen

Um Differentiale in Zylinderkoordinaten zu transformieren kann die Jacobi-Matrix der Koordinatentransformation betrachtet werden.

Jacobi-Matrix und Funktionaldeterminante

Die Jacobi-Matrix besitzt folgende Form:

$J=\frac{\partial (x,y,z)}{\partial (r,\phi,z}=\left( \begin{array}{ccc} \cos{\phi}&-r\cdot\sin{\phi}&0\\ \sin{\phi}&r\cdot\cos{\phi}&0\\ 0&0&1\\ \end{array} \right)$

Die Funktionaldeterminante lautet demnach:

det J=r

Differentiale (Volumenelement, Flächenelement, Linienelement)

Die Differentiale lassen sich nun mithilfe der Jacobi-Matrix durch folgende Abbildung angeben:

$\left( \begin{array}{ccc} \mathrm{d} x\\ \mathrm{d} y\\\mathrm{d} z\\ \end{array} \right)=J\cdot\left( \begin{array}{ccc} \mathrm{d} r\\\mathrm{d}\phi \\\mathrm{d}z \\ \end{array} \right)$

Mit der Funktionaldeterminante lässt sich außerdem ganz einfach das Volumenelement $\mathrm{d}V$ bestimmen:

$\mathrm{d}V=\mathrm{det}J\cdot\mathrm{d}z \mathrm{d}\phi \mathrm{d}r=r\cdot \mathrm{d}z \mathrm{d}\phi \mathrm{d}r$

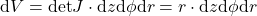
Daraus ergibt sich durch Differentiation das Flächenelement $\mathrm{d}A$ :

$\mathrm{d}A=\frac{\mathrm{d}V}{\mathrm{d}r}=r\cdot \mathrm{d}z \mathrm{d}\phi$

Für das Linienelement $\mathrm{d}s$ gilt:

$\mathrm{d}s^2=\mathrm{d}x^2+\mathrm{d}y^2+\mathrm{d}z^2=\mathrm{d}r^2+r^2\mathrm{d}\phi^2+\mathrm{d}z^2$

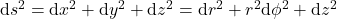
Transformation von Basisvektoren und Vektoroperatoren

Im Folgenden sollen die Einheitsvektoren sowie der Nabla– und der Laplaceoperator in Zylinderkoordinaten bestimmt werden.

Einheitsbasisvektoren

Aus dem allgemeinen Richtungsvektor $\vec{r}=\left( \begin{array}{ccc} r\cdot\cos{\phi}\\r\cdot\sin{\phi} \\z\\ \end{array} \right)$ lassen sich die Einheitsvektoren in Zylinderkoordinaten herleiten:

$\vec{e_r}=\frac{\frac{\partial\vec{r}}{\partial r}}{\left\vert\frac{\partial\vec{r}}{\partial r}}\right\vert}=\left( \begin{array}{ccc} \cos{\phi}\\\sin{\phi} \\0 \\ \end{array} \right)$

$\vec{e_{\phi}}=\frac{\frac{\partial\vec{r}}{\partial \phi}}{\left\vert\frac{\partial\vec{r}}{\partial \phi}}\right\vert}=\left( \begin{array}{ccc} -\sin{\phi}\\\cos{\phi} \\0 \\ \end{array} \right)$

$\vec{e_{z}}=\frac{\frac{\partial\vec{r}}{\partial z}}{\left\vert\frac{\partial\vec{r}}{\partial z}}\right\vert}=\left( \begin{array}{ccc} 0\\0 \\1\\ \end{array} \right)$

Quiz zum Thema Zylinderkoordinaten

Partielle Ableitungen (Nabla- und Laplaceoperator)

Die partiellen Ableitungen in Zylinderkoordinaten sind durch folgende Abbildung gegeben:

$\left(\frac{\partial}{\partial r}, \frac{\partial}{\partial \phi},\frac{\partial}{\partial z} \right)=\left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y},\frac{\partial}{\partial z} \right)\cdot J$

$\left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y},\frac{\partial}{\partial z} \right)=\left(\frac{\partial}{\partial r}, \frac{\partial}{\partial \phi},\frac{\partial}{\partial z} \right)\cdot J^{-1}$

Der Nabla-Operator in Zylinderkoordinaten besitzt die folgende Form:

$\nabla=\vec{e_r}\frac{\partial}{\partial r}+\vec{e_{\phi}}\frac{1}{r}\frac{\partial}{\partial \phi}+\vec{e_z}\frac{\partial}{\partial z}$

Der Nabla-Operator in dieser Form kann dann auf Skalarfelder angewandt werden, um den Gradienten in Zylinderkoordinaten zu bestimmen.

Für die Divergenz in Zylinderkoordinaten eines Vektorfeldes $\vec{A}=A_r\cdot \vec{e_r}+A_{\theta}\cdot\vec{e_{\theta}}+A_{\phi}\cdot\vec{e_{\phi}}$ gilt:

$\nabla \cdot\vec{A}=\frac{1}{r}\frac{\partial}{\partial r}(r\, A_r)+\frac{1}{r}\frac{\partial A_{\phi}}{\partial\phi}+\frac{\partial A_z}{\partial z}$

Für ein solches Vektorfeld sieht die Rotation in Zylinderkoordinaten folgendermaßen aus:

$\nabla \times\vec{A}=\left(\frac{1}{r}\frac{\partial A_z}{\partial\phi}-\frac{\partial A_{\phi}}{\partial z}\right)\vec{e_r}+\left(\frac{\partial A_{r}}{\partial z}-\frac{\partial A_z}{\partial r}\right)\vec{e_{\phi}}+\frac{1}{r}\left(\frac{\partial}{\partial r}(r\, A_{\phi})-\frac{\partial A_r}{\partial \phi}\right)\vec{e_{z}}$

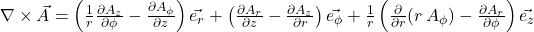
Setzt man nun in die Formel für die Divergenz als Vektorfeld den Nabla-Operator ein, so erhält man den Laplace-Operator:

$\triangle=\nabla ^2=\frac{1}{r}\frac{\partial}{\partial r}+\frac{\partial ^2}{\partial r^2}+\frac{1}{r^2}\frac{\partial ^2}{\partial\phi ^2}+\frac{\partial ^2}{\partial z ^2}$

zur Videoseite: Zylinderkoordinaten

Beliebte Inhalte aus dem Bereich Analysis

Polarkoordinaten

Zylinderkoordinaten

Kugelkoordinaten

Satz von Stokes

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .