Wie merke ich beim Umformen in eine Potenz, ob der Exponent positiv oder negativ wird?

Beim Umformen wird der Exponent negativ, wenn der Ausdruck unter der Wurzel im Nenner steht. Steht die Wurzel im Zähler, bleibt der Exponent positiv. Das liegt daran, dass . Beispiel: , aber .

Welche Fehler passieren am häufigsten, wenn ich bei Wurzelfunktionen den neuen Exponenten ausrechne?

Am häufigsten wird der Bruch-Exponent falsch gebildet, weil m und n vertauscht oder Klammern vergessen werden. Bei gilt immer , nicht . Außerdem wird bei oft vergessen, dass ist, also .

Wie prüfe ich schnell, ob meine Stammfunktion stimmt, ohne alles nochmal zu rechnen?

Du prüfst schnell, indem du deine Stammfunktion einmal ableitest und schaust, ob wieder die Ausgangsfunktion entsteht. Nutze dazu die Potenzregel: . Beispiel: Aus wird .

Was mache ich, wenn unter der Wurzel nicht nur x steht, sondern zum Beispiel 3x oder x + 2?

Dann brauchst du meist eine Substitution, weil die einfache Potenzregel nicht direkt passt. Für kannst du ausklammern und wie bei integrieren. Bei setze , dann wird .

Video

Quiz

Hier geht's zum Video „Stammfunktion bilden“

Stammfunktion Wurzel x

Wichtige Inhalte in diesem Video

Stammfunktion Wurzel x einfach erklärt

(00:12)

Stammfunktion Wurzel x aufstellen

(00:59)

Weitere Beispiele

(01:58)

Du willst wissen, wie du die Stammfunktion Wurzel x berechnest? In diesem Beitrag und in unserem Video erklären wir dir alles, was du dazu wissen musst!

Inhaltsübersicht

Stammfunktion Wurzel x einfach erklärt

im Videozur Stelle im Video springen

(00:12)

Eine Stammfunktion der Wurzel x ist:

F(x) = $\frac{2}{3}\cdot\displaystyle x^{\frac{3}{2}}$

Um allgemein Stammfunktionen von Wurzel x und anderen Wurzelfunktionen zu bestimmen, musst du die Wurzel in eine Potenz umzuwandeln. Das funktioniert so:

f(x) = $\displaystyle \sqrt[\scriptstyle \color {blue}n]{x^{\color {red}m}}$ = $x^{\frac {\color {red}m}{\color {blue}n}}$

Die Werte m und n setzt du dann in die folgende Gleichung der Stammfunktion ein:

F(x) = $\dfrac{1}{\frac{\color {red}m}{\color {blue}n} + 1} \cdot \displaystyle x^{\frac{\color {red}m}{\color {blue}n} + 1}$ + C

Merke: Vergiss nicht die Konstante C bei der Stammfunktion!

Stammfunktion Wurzel x aufstellen

im Videozur Stelle im Video springen

(00:59)

Damit du die Formel besser verstehst, probiere gleich mal ein Beispiel. Stelle die Stammfunktion der folgenden Wurzelfunktion auf:

f(x) = $\displaystyle \sqrt[\scriptstyle \color {blue}3]{x^{\color {red}2}}$

Schritt 1: Wurzel in Potenzform umformen

Zu Beginn der Rechnung musst du die Wurzel in eine Potenzfunktion umwandeln.

f(x) = $\displaystyle \sqrt[\scriptstyle \color {blue}n]{x^{\color {red}m}}$ = $x^{\frac {\color {red}m}{\color {blue}n}}$

f(x) = $\displaystyle \sqrt[\scriptstyle \color {blue}3]{x^{\color {red}2}}$ = $x^{\frac {\color {red}2}{\color {blue}3}}$

Schritt 2: Stammfunktion aufstellen

Nun musst du den Exponenten, den Bruch $\dfrac{\color {red}2}{\color {blue}3}$ , in die allgemeine Stammfunktion einsetzen. Im Exponenten und Nenner musst du die Werte addieren.

F(x) = $\dfrac{1}{\frac{\color {red}m}{\color {blue}n} + 1}\cdot\displaystyle x^{\frac{\color {red}m}{\color {blue}n} + 1}$ + C

F(x) = $\dfrac{1}{\frac{\color {red}2}{\color {blue}3} + 1}\cdot\displaystyle x^{\frac{\color {red}2}{\color {blue}3} + 1}$ = $\dfrac{1}{\frac{5}{3}}\cdot\displaystyle x^{\frac{5}{3}}$ + C

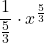F(x) = $\frac{3}{5}\cdot\displaystyle x^{\frac{5}{3}}$ + C

Merke: Aus dem Bruch $\dfrac{1}{\frac{5}{3}}$ ergibt sich $\dfrac{3}{5}$ . Denn Brüche dividierst du, indem du mit dem Kehrwert multiplizierst.

Schritt 3: Wurzelfunktion zusammenfassen

Um die Aufgabe abzuschließen, musst du die Gleichung jetzt wieder in eine Wurzelfunktion umformen. Nutze dafür: $x^{\frac {\color {red}m}{\color {blue}n}}$ = $\displaystyle \sqrt[\scriptstyle \color {blue}n]{x^{\color {red}m}}$

F(x) = $\frac{3}{5}\cdot\displaystyle x^{\frac{\color {red}5}{\color {blue}3}}$ + C

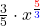F(x) = $\frac{3}{5}\cdot\displaystyle \sqrt[\scriptstyle \color {blue}3]{x^{\color {red}5}}$ + C

Und das ist dein Ergebnis! Du weißt jetzt, wie du die Stammfunktion der Wurzel x berechnest. Dieses Verfahren kannst du jetzt auf sämtliche Wurzelfunktionen übertragen.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Weitere Beispiele

im Videozur Stelle im Video springen

(01:58)

Beispiel 2: Fehlender Exponent

f(x) = $\displaystyle \sqrt[\scriptstyle \color {blue}4]{x^{}}$ = $\displaystyle x^{\frac{\color {red}1}{\color {blue}4}}$

F(x) = $\dfrac{1}{\frac{\color {red}1}{\color {blue}4} + 1}\cdot\displaystyle x^{\frac{\color {red}1}{\color {blue}4} + 1}$ = $\frac{4}{5}\cdot\displaystyle x^{\frac{5}{4}}$ + C

F(x) = $\frac{4}{5}\cdot\displaystyle \sqrt[\scriptstyle 4]{x^{5}}$ + C

Merke: Ist in der Wurzel kein Exponent, musst du dafür 1 einsetzen.

Expertenbeispiel: Bruch als Exponent

f(x) = $\displaystyle \sqrt[\scriptstyle 5]{x^{\frac{1}{2}}}$ = $\displaystyle x^{\frac{\frac {1}{2}}{5}}$ = $\displaystyle x^{\frac{\color {red}1}{\color {blue}10}}$

F(x) = $\dfrac{1}{\frac{\color {red}1}{\color {blue}10} + 1}\cdot\displaystyle x^{\frac{\color {red}1}{\color {blue}10} + 1}$ = $\frac{10}{11}\cdot\displaystyle x^{\frac{11}{10}}$ + C

F(x) = $\frac{10}{11}\cdot\displaystyle \sqrt[\scriptstyle 10]{x^{11}}$ + C

Übrigens: Ist der Exponent ein Bruch, kann dieser während der Umformung gelöst werden. So wird aus $\displaystyle \frac{\frac {1}{2}}{5}$ = $\displaystyle \frac{1}{10}$ .

Stammfunktion Wurzel x — häufigste Fragen

(ausklappen)

Wie merke ich beim Umformen in eine Potenz, ob der Exponent positiv oder negativ wird?

Beim Umformen wird der Exponent negativ, wenn der Ausdruck unter der Wurzel im Nenner steht. Steht die Wurzel im Zähler, bleibt der Exponent positiv. Das liegt daran, dass $\frac{1}{x^a}=x^{-a}$ . Beispiel: $\frac{1}{\sqrt{x}}=x^{-1/2}$ , aber $\sqrt{x}=x^{1/2}$ .
Welche Fehler passieren am häufigsten, wenn ich bei Wurzelfunktionen den neuen Exponenten ausrechne?

Am häufigsten wird der Bruch-Exponent falsch gebildet, weil m und n vertauscht oder Klammern vergessen werden. Bei $\sqrt[n]{x^m}$ gilt immer $x^{m/n}$ , nicht $x^{n/m}$ . Außerdem wird bei $\sqrt[n]{x}$ oft vergessen, dass ist, also $x^{1/n}$ .
Wie prüfe ich schnell, ob meine Stammfunktion stimmt, ohne alles nochmal zu rechnen?

Du prüfst schnell, indem du deine Stammfunktion einmal ableitest und schaust, ob wieder die Ausgangsfunktion entsteht. Nutze dazu die Potenzregel: $\frac{d}{dx}\left(a\cdot x^p\right)=a\cdot p\cdot x^{p-1}$ . Beispiel: Aus $F(x)=\frac{2}{3}x^{3/2}$ wird $F'(x)=\sqrt{x}$ .
Was mache ich, wenn unter der Wurzel nicht nur x steht, sondern zum Beispiel 3x oder x + 2?

Dann brauchst du meist eine Substitution, weil die einfache Potenzregel nicht direkt passt. Für $\sqrt{3x}$ kannst du $3^{1/2}\sqrt{x}$ ausklammern und wie bei $\sqrt{x}$ integrieren. Bei $\sqrt{x+2}$ setze , dann wird $\int\sqrt{x+2}\,dx=\int u^{1/2}\,du=\frac{2}{3}u^{3/2}+C$ .

Stammfunktion bilden

Super gemacht! So schnell kannst du die Bildung von Stammfunktion der Wurzel x lernen. Falls du noch mehr über Stammfunktionen und ihre Anwendungsbeispiele wissen willst, schau dir gern dieses Video an.