Ableitung bestimmter Funktionen
Du möchtest schnell verstehen, wie du wichtige Funktionen ableiten kannst? Dann ist unser Video genau das Richtige für dich!
Die Themen Ableitung und Ableitungsregeln erklären wir dir ausführlich in extra Videos!
Inhaltsübersicht
Übersicht Ableitung wichtiger Funktionen
| Funktion | Ableitung | |
| Wurzel ableiten |  |
 |
| Cosinus ableiten |  |
 |
| Sinus ableiten |  |
 |
| Tangens ableiten |  |
 |
| e Funktion ableiten |  |
 |
| ln ableiten |  |
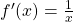 |
Wurzelfunktion ableiten
Im folgenden zeigen wir dir, wie du eine Wurzelfunktion ableiten kannst.
Die Wurzelfunktion
![Rendered by QuickLaTeX.com f(x) = \sqrt[n]{x}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fd9a6df9f122fc4e742d437cfeedc1f5_l3.png)
kannst du auch schreiben als
 .
.
Damit haben wir die Form „Zahl mal x hoch eine andere Zahl“. Eine solche Form kannst du durch Verwendung der Regel „Exponent vor das x ziehen und dann den Exponenten bei x um eins reduzieren“ ableiten.
Das Ableiten der Wurzelfunktion ![Rendered by QuickLaTeX.com f(x) = \sqrt[n]{x}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fd9a6df9f122fc4e742d437cfeedc1f5_l3.png) ergibt
ergibt
 .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel
Betrachte die Wurzelfunktion

Das Ableiten ergibt
 .
.
Trigonometrischer Funktionen ableiten
Nun zeigen wir dir die Ableitungen der trigonometrischen Funktionen Sinus, Kosinus und Tangens.
Für den Sinus

ergibt das Ableiten
 .
.
Diese Ableitung musst du dir gut einprägen. In unserem Artikel über das Sinus ableiten , zeigen wir dir mehrere Beispiele dazu.
Für den Cosinus

ergibt das Ableiten
 .
.
Beachte, dass hier ein Minuszeichen vorkommt. Beim Ableiten vom Sinus hingegen kommt kein Minuszeichen vor. Auch zum Ableiten des Kosinus haben wir einen ausführlichen Artikel für dich vorbereitet mit Erklärungen und mehreren Beispielen.
Für den Tangens

ergibt das Ableiten
 .
.
Du möchtest mehr über die Ableitung des Tangens erfahren und mehrere Beispiele durchrechnen? Dann schau dir unser Video dazu an!
Ableitung e-Funktion und ln-Funktion
Schauen wir uns nun einmal die Ableitung der e Funktion und der ln Funktion an.
Für die e-Funktion

ergibt das Ableiten
 .
.
Beachte, dass die Ableitung gerade wieder die Funktion selbst ist. Das Ableiten der e-Funktion ergibt also wieder die e-Funktion. Erst wenn im Exponenten der e Funktion ein anderer Ausdruck als nur x steht, wird das Ableiten komplizierter. Dann musst du die Kettenregel anwenden.
Beispiel
Ein Beispiel für das Ableiten einer komplizierteren e Funktion wäre

Wie das genau funktioniert und viele Beispiele zum Ableiten der e Funktion findest du in einem eigenen Beitrag .
Für die ln-Funktion

ergibt das Ableiten
 .
.
Falls du einen Logarithmus ableiten möchtest, der nicht nur x im Argument stehen hat, benötigst du zusätzlich die Kettenregel.
Beispiel
Ein solcher Fall wäre die Funktion
 .
.
Das Ableiten liefert
 .
.
Falls du noch mehr Beispiele zum Logarithmus Ableiten berechnen möchtest, sieh dir unseren Beitrag dazu an.
