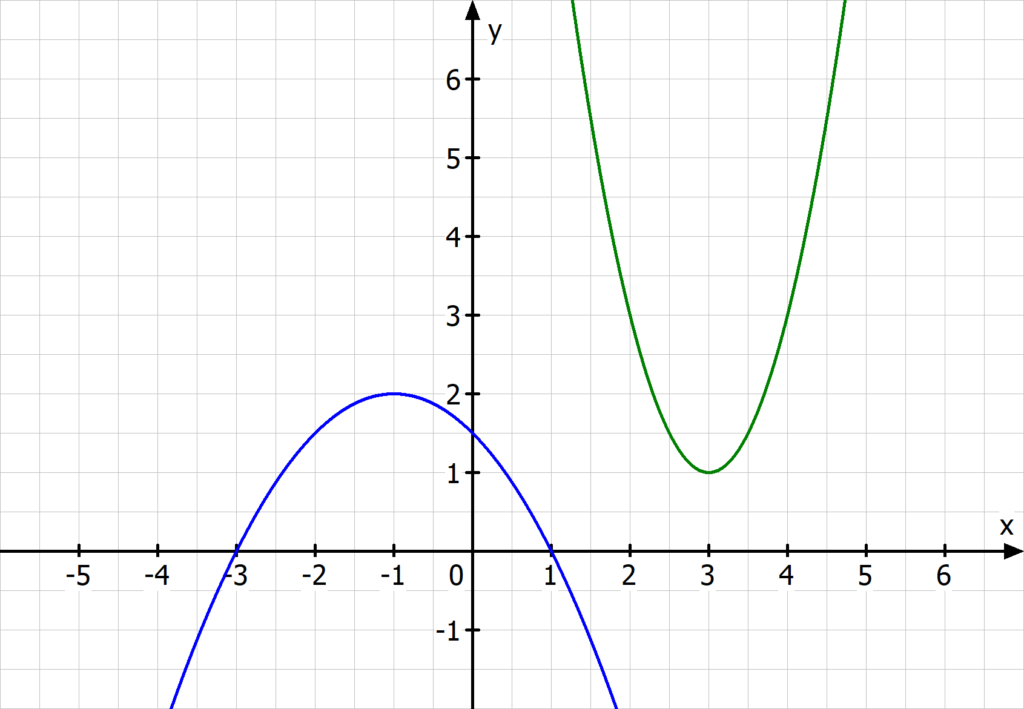
Krümmungsverhalten
Wie kannst du das Krümmungsverhalten einer Funktion berechnen? Beschreibt sie eine Linkskurve oder eine Rechtskurve? Alles, was du über die Krümmung einer Funktion wissen musst, erfährst du hier im Beitrag und im zugehörigen Video .
Inhaltsübersicht
Krümmungsverhalten — das Wichtigste auf einen Blick
Die Krümmung einer Funktion f kannst du an ihrer zweiten Ableitung f“ ablesen:
- f“(x) < 0 → f rechtsgekrümmt (konkav) an der Stelle x
- f“(x) > 0 → f linksgekrümmt (konvex) an der Stelle x
- f“(x) = 0 → keine Krümmung an der Stelle x
Krümmung berechnen
Um das Krümmungsverhalten einer Funktion f herauszufinden, musst du also zunächst ihre zweite Ableitung f“ berechnen. Dabei gibt es drei Möglichkeiten, wie sie aussehen kann:
- f“(x) ist eine negative Zahl (z. B. f“(x) = – 2) → f ist überall rechtsgekrümmt.
- f“(x) ist eine positive Zahl (z. B. f“(x) = 6) → f ist überall linksgekrümmt.
- f“(x) enthält noch ein x → Es kann sein, dass f sein Krümmungsverhalten an den Nullstellen von f“(x) ändert.
Schau dir nun genauer an, wie du in den einzelnen Fällen die Krümmung berechnest.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Krümmungsverhalten berechnen — rechtsgekrümmt
Du hast zum Beispiel die Funktion f(x) = – x2 gegeben und sollst ihr Krümmungsverhalten berechnen. Dazu bestimmst du zunächst die zweite Ableitung f“(x):
- f(x) = – x2
- f'(x) = – 2x
- f“(x) = – 2 < 0
f“(x) ist also für jedes x negativ. Damit ist der Graph von f(x) = – x2 überall rechtsgekrümmt.
Krümmungsverhalten berechnen — Linksgekrümmt
Betrachte nun die Funktion f(x) = 3x2
- f(x) = 3x2
- f'(x) = 6x
- f“(x) = 6 > 0
f“(x) ist dieses Mal immer eine positive Zahl. Daher ist der zugehörige Graph eine einzige Linkskurve.
- Stell dir vor, der Funktionsgraph ist ein Weg auf dem du mit dem Fahrrad fährst. In welche Richtung musst du lenken?
- Nach rechts → Rechtsgekrümmte Funktion
- Nach links → Linksgekrümmte Funktion
- Du kannst dich auch an den Buchstaben in den Wörtern orientieren:
- f“(x) negativ → rechtskrümmt
- f“(x) positiv → linkskrümmt
- Die Fachbegriffe konkav und konvex kannst du dir zum Beispiel mit folgenden Sprüchen merken:
- „Konkav ist der Buckel vom Schaf.“
- „Konvex ist der Kochtopf von der Hex.“
Krümmung berechnen — Linkskurve und Rechtskurve
Was passiert aber, wenn in der zweiten Ableitung noch ein x auftaucht? Am Beispiel der Funktion f(x) = x3 + 3x2 zeigen wir dir, wie du in so einem Fall vorgehst.
Um die Krümmung zu berechnen, musst du auch hier zuerst die zweite Ableitung bilden:
- f(x) = x3 + 3x2
- f'(x) = 3x2 + 6x
- f“(x) = 6x + 6
Das Krümmungsverhalten ist jetzt nicht an jeder Stelle x dasselbe. Du musst dich also fragen:
Für welche x ist f“(x) = 6x + 6 kleiner als 0? Dazu löst du die Ungleichung 6x + 6 < 0.
6x + 6 < 0
⇔ 6x < -6
⇔ x < -1
Für alle x < -1 ist also f“(x) < 0. Damit ist f rechtsgekrümmt (konkav) für alle x, die kleiner als -1 sind.
Um die Stellen zu finden, wo die Funktion eine Linkskurve macht, löst du die umgekehrte Ungleichung:
6x + 6 > 0
⇔ 6x > -6
⇔ x > -1
Das bedeutet: f ist linksgekrümmt (konvex) für alle x, die größer als -1 sind.
Zwischen der Rechts– und der Linkskurve gibt es eine Stelle x, wo die Funktion keine Krümmung hat. Dort gilt f“(x) = 0. (Hier: f(-1) = 0). Solche Punkte, wo die Funktion ihr Krümmungsverhalten ändert, nennst du Wendepunkte. Eine Funktion kann auch mehrere Wendepunkte haben und damit mehrmals ihre Krümmung wechseln.
Achtung: Bei der Funktion f(x) = x4 kommt in der zweiten Ableitung f“(x) = 12x2 auch ein x vor. An der Stelle x = 0 ist f“(x) = 0. Davor und danach ist f“(x) aber immer positiv (denn x2 ist nie negativ). Der Funktionsgraph von f(x) = x4 ist also eine einzige Linkskurve und ändert sein Krümmungsverhalten nicht!
Wendepunkt berechnen
Klasse! Wenn in Mathe die Begriffe konvex und konkav auftauchen, weißt du nun Bescheid. Das Krümmungsverhalten einer Funktion zu berechnen ist jetzt kein Problem mehr für dich! Aber was genau hat es mit diesen Wendepunkten auf sich? Mehr dazu erfährst du in unserem Video !