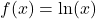Ableitung
Was ist die Ableitung in Mathe und wie kannst du sie dir anschaulich vorstellen? Das erfährst du hier im Artikel und in unserem Video !
Inhaltsübersicht
Ableitung einfach erklärt
Die Ableitung f'(x) einer Funktion f(x) gibt die Steigung der Funktion in einem bestimmten Punkt an. Du unterscheidest drei Fälle:
- Ableitung positiv f'(x) > 0 → Funktion steigt
- Ableitung negativ f'(x) < 0 → Funktion fällt
- Ableitung null f'(x) = 0 → Funktion hat einen Extrempunkt (Hochpunkt oder Tiefpunkt) oder einen Sattelpunkt
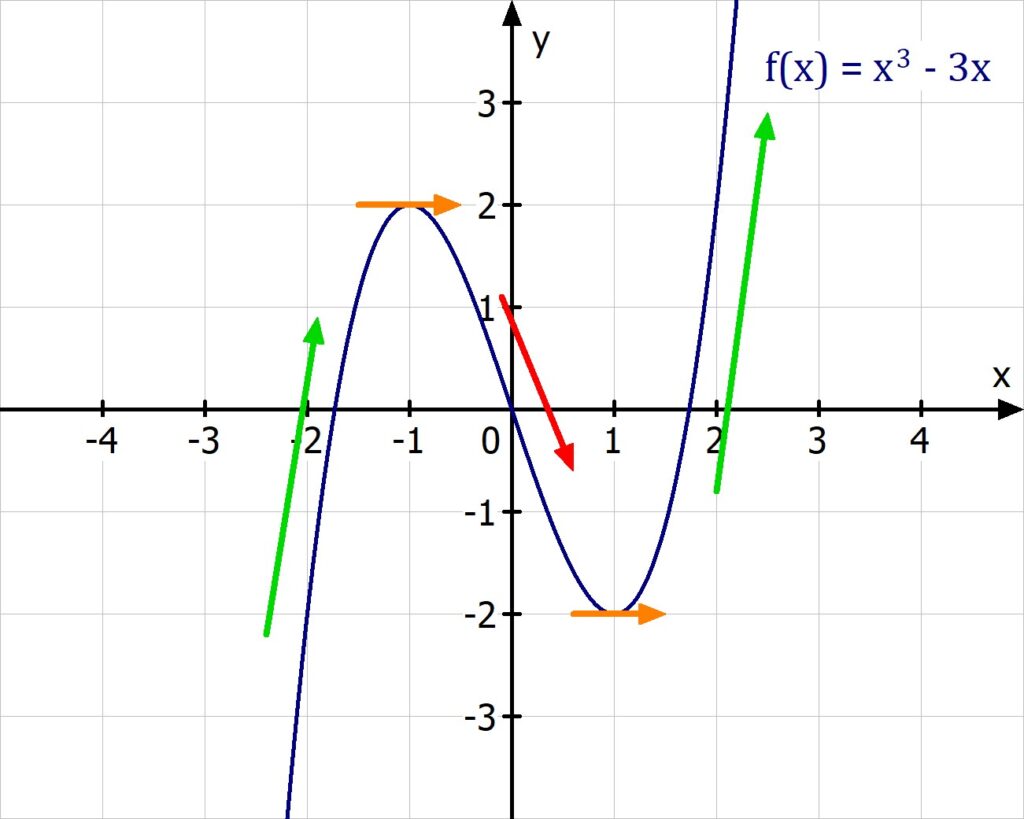
Das siehst du gut am Beispiel f(x) = x3 – 3x. Die Ableitung davon ist f'(x) = 3x2 – 3.
- An x = -1,5 steigt die Funktion → f'(-1,5) = 3,75 > 0
- An x = 0,5 fällt die Funktion → f'(0,5) = -2,25 < 0
- An x = 1 hat die Funktion einen Tiefpunkt → f'(1) = 0
Du brauchst Ableitungen in Mathe vor allem bei der Kurvendiskussion, um auszurechnen, wo die Extremstellen einer Funktion liegen.
Graphische Ableitung
Du kannst von Funktionen die Ableitung bilden, ohne dabei zu rechnen. Das nennst du graphische Ableitungen. Dabei schaust du dir den Graphen deiner Funktion f(x) an und zeichnest daraus den Graphen der Ableitung f'(x). Das machst du so:
- Die Extremstellen (E) der Funktion werden die Nullstellen (N) der Ableitung (hier: -1 und 1)
- Die Wendestellen (W) der Funktion werden die Extremstellen (E) der Ableitung (hier: 0)
Die so entstandenen Nullstellen und Extrempunkte verbindest du dann zu einer Kurve — dem Graphen deiner Ableitung.
Du kannst dir graphische Ableitungen mithilfe einer Tabelle und der Eselsbrücke „NEW“ ganz leicht merken. Für die Nullstellen N, die Extremstellen E und die Wendestellen W gilt:
| f(x) | N | E | W | |
| f'(x) | N | E | W |
Punkte, die in der Tabelle übereinander stehen, sind jeweils gleich. Du siehst also, dass die Extremstellen der Funktion gleich den Nullstellen der Ableitung sind. Ebenso sind die Wendestellen der Funktion die Extremstellen der Ableitung.
Die erste Ableitung gibt die Steigung des Graphen von f(x) an einem Punkt an. Mit der Ableitung kannst du also an jeder Stelle x die Steigung der Funktion ermitteln. Wenn du einen x-Wert (z.B. x = 5) in die erste Ableitung einsetzt, erhältst du die Steigung der Funktion in diesem Punkt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Expertenwissen: Was ist die Ableitung?
Du weißt jetzt schon, dass die Ableitung die Steigung in einem Punkt angibt. Aber was bedeutet Steigung eigentlich?
Mit „Steigung in einem Punkt“ meinst du immer die Steigung der Tangente . Das ist eine Gerade, die den Graphen in dem Punkt berührt. Hier siehst du zum Beispiel die Tangente an der Stelle x = 1. Ihre Steigung ist dann gleich der Steigung der Funktion an der Stelle x = 1.
Aber wie kannst du die Tangentensteigung ermitteln? Schau dir das in nur 2 Schritten an:
Schritt 1: Berechne die Steigung einer Sekante
Eine Sekante ist eine Gerade, die den Graph in zwei Punkten schneidet:
- Einer davon ist der Punkt, in dem du die Ableitung berechnen willst. Du kannst ihn allgemein P(x0|y0) nennen.
- Der andere Punkt liegt zum Beispiel weiter rechts. Nenn ihn einfach mal Q(x|y).
Die Sekante ist eine Gerade . Um ihre Steigung m zu berechnen , teilst du den Abstand der y-Werte der beiden Punkte durch den Abstand der x-Werte (Steigungsdreieck ):
![Rendered by QuickLaTeX.com \[m=\frac{\textcolor{olive}{y}-\textcolor{purple}{y_0}}{\textcolor{olive}{x}-\textcolor{purple}{x_0}}=\frac{f(\textcolor{olive}{x})-f(\textcolor{purple}{x_0})}{\textcolor{olive}{x}-\textcolor{purple}{x_0}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1a7e68a3e7b2a8b179cb52912f42a19b_l3.png)
Schritt 2: Berechne die Steigung der Tangente
Jetzt willst du von der Sekante zu einer Tangente an der Stelle x0 kommen. Dazu verkleinerst du den Abstand zwischen x und x0 immer weiter.
Mathematisch schreibst du dafür den Limes (Grenzwert ) von x gegen x0:
![Rendered by QuickLaTeX.com \[\lim_{x\to x_0}\frac{f(\textcolor{olive}{x})-f(\textcolor{purple}{x_0})}{\textcolor{olive}{x}-\textcolor{purple}{x_0}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ec7d160f65c90435d3f1930ad451fbc7_l3.png)
![Rendered by QuickLaTeX.com \[f'(x_0) = \lim_{x\to x_0}\frac{f(\textcolor{olive}{x})-f(\textcolor{purple}{x_0})}{\textcolor{olive}{x}-\textcolor{purple}{x_0}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-905e7088b94ce373271128f720b745ab_l3.png)
Es gibt Funktionen, die nicht überall eine Ableitung haben. Die Funktion f(x) = |x| hat zum Beispiel einen Knick an der 0 und hat deshalb an diesem Punkt keine Ableitung. Bei Funktionen ohne Knicke kannst überall die Ableitung bilden. Du nennst sie differenzierbar .
Höhere Ableitungen und Notation
Von der Ableitung f'(x) einer Funktion kannst du auch nochmal die Ableitung bilden. Du erhältst dann die zweite Ableitung f“(x). Sie gibt die Krümmung der Funktion an. Außerdem kannst du mit zweiten Ableitungen Wendepunkte berechnen.
- erste Ableitung: f'(x)
- zweite Ableitung: f“(x)
Hier siehst du nochmal die Funktion f(x) = x3 – 3x, ihre erste Ableitung f'(x) = 3x2 – 3 und die zweite Ableitung f“(x) = 6x.
Meistens musst du nur die ersten und zweiten Ableitungen berechnen. Es gibt aber noch höhere Ableitungen:
- dritte Ableitung: f“'(x)
- vierte Ableitung: f(4)(x)
- …
- n-te Ableitung: f(n)(x)
Du siehst, dass du ab der vierten Ableitung nicht mehr die Striche hinter dem f verwendest. Stattdessen gibst du in Klammern die Anzahl der Ableitung an.
Übrigens: Anstatt f'(x) kannst du auch  schreiben (sprich: d f nach d x). Das
schreiben (sprich: d f nach d x). Das  gibt hier an, dass x die Variable ist, nach der du f ableitest. Das ist vor allem dann wichtig, wenn es mehrere Variablen gibt. In der Physik willst du außerdem oft nach der Zeit t ableiten. Dann schreibst du
gibt hier an, dass x die Variable ist, nach der du f ableitest. Das ist vor allem dann wichtig, wenn es mehrere Variablen gibt. In der Physik willst du außerdem oft nach der Zeit t ableiten. Dann schreibst du  oder auch
oder auch  .
.
Das Integral (bzw. die Stammfunktion) ist die „Gegenrichtung“ zur Ableitung. Wenn du eine Funktion erst ableitest und dann integrierst, kommt wieder die ursprüngliche Funktion heraus (bis auf eine Zahl, die mit + dahinter stehen kann). Diesen Zusammenhang nennst du auch Hauptsatz der Integral – und Differenzialrechnung .
Ableitungsregeln
Um die Ableitung einer Funktion zu berechnen
, verwendest du einige Ableitungsregeln
, zum Beispiel für Potenzfunktionen xp:
Beispiel: f(x) = x2 + 3x → f'(x) = 2x+ 3
Mit anderen Ableitungsregeln kannst du beispielsweise die Exponentialfunktion und die Logarithmusfunktion ableiten.
In der Tabelle siehst du schon mal alle Ableitungsregeln auf einen Blick:
| Ableitungsregel | Funktion | Ableitung |
| Summenregel |  |
 |
| Differenzregel |  |
 |
| Produktregel |  |
 |
| Quotientenregel |  |
![Rendered by QuickLaTeX.com f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1128d60300515aa8b8df5c88d4dbbdf9_l3.png) |
| Kettenregel |  |
 |
| Potenzregel |  |
 |
| Faktorregel | 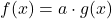 |
 |
Schau dir die einzelnen Regeln gleich genauer an!
Potenzregel
Mit der Potenzregel kannst du von Funktionen die Ableitung bilden, die nur aus x mit einer Hochzahl bestehen, zum Beispiel x2, x3 und so weiter. Für die Ableitung ziehst du die Hochzahl nach vorne und verringerst dann die Hochzahl um 1:
- f(x) = x2 → f'(x) = 2x2–1 = 2x
- f(x) = x3 → f'(x) = 3x3–1 = 3x2
Faktor- und Summenregel
Die Faktorregel brauchst du, wenn vor dem x eine Zahl steht, zum Beispiel bei 3x4. Die Zahl lässt du dann einfach stehen und leitest den Rest der Funktion ab:
- f(x) = 3x4 → f'(x) = 3 · 4x3
Die Summenregel verwendest du, wenn du eine Summe ableiten sollst, zum Beispiel f(x) = x2 + 3x. Hier leitest du jeden Teil einzeln ab:
- f(x) = x2 + 3x → f'(x) = 2x + 3
Produktregel
Die Produktregel brauchst du, wenn deine Funktion ein Produkt ist (eine Malrechnung).Zum Beispiel hier:
f(x) = x2 • cos(x)
Der erste Faktor des Produkts ist u(x), also hier u(x) = x2, und der zweiten Faktor v(x), also v(x) = cos(x). Mit der Produktregel gilt dann:
f'(x) = u(x) • v'(x) + u'(x) • v(x)
Im Beispiel musst du also zuerst von u und v die Ableitungen berechnen:
- u(x) = x2 → u'(x) = 2x
- v(x) = cos(x) → v'(x) = -sin(x)
Mit der Produktregel kannst du dann die Ableitung f'(x) aufschreiben:
f'(x) = x2 • -sin(x) + 2x • cos(x)
Das ging dir zu schnell? Dann schau dir hier die Produktregel nochmal in Ruhe an!
Quotientenregel
Mit der Quotientenregel kannst du von Brüchen die Ableitungen berechnen, zum Beispiel:
![Rendered by QuickLaTeX.com \[f(x) = \frac{\textcolor{blue}{x^2}}{\textcolor{red}{\cos(x)}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0d0707b92261df08789290529b2366a9_l3.png)
Der obere Teil (Zähler) heißt g(x), hier also g(x) = x2, und der untere Teil (Nenner) h(x). Hier ist also h(x) = cos(x). Dann ist die Ableitung allgemein:
![Rendered by QuickLaTeX.com \[ f'(x) = \frac{\textcolor{red}{h(x)}\cdot \textcolor{teal}{g'(x)} - \textcolor{orange}{h'(x)} \cdot \textcolor{blue}{g(x)}}{\textcolor{red}{h(x)}^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e9a69d0bf4ee21b0a22e1ee795aa2b57_l3.png)
Im Beispiel musst du also erstmal von g und h die Ableitungen berechnen:
- g(x) = x2 → g'(x) = 2x
- h(x) = cos(x) → h'(x) = -sin(x)
![Rendered by QuickLaTeX.com \[ f'(x) = \frac{\textcolor{red}{\cos(x)}\cdot \textcolor{teal}{2x} - \textcolor{orange}{\-sin(x)} \cdot \textcolor{blue}{x^2}}{\textcolor{red}{\cos(x)}^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3b8c85ae8f792b743f18cbfca935e08c_l3.png)
Wenn du noch mehr zur Quotientenregel erfahren willst, dann schau hier vorbei!
Kettenregel
Die Kettenregel verwendest du, wenn eine Funktion innerhalb einer anderen steht („verkettete“ Funktionen). Schau dir ein Beispiel an:
h(x) = sin(3x + 5)
Die Funktion f(x) = 3x + 5 steht innerhalb der Sinusfunktion. Die äußere Funktion kannst du mit g(y) = sin(y) bezeichnen. Dann ist die Ableitung von h(x):
h'(x) = g‘(f(x)) • f'(x)
Hier ist f(x) = 3x + 5 und g(y) = sin(y). Somit erhältst du f'(x) = 3 und g'(y) = cos(y). Insgesamt ist die Ableitung:
h'(x) = cos(3x + 5) • 3
Schau dir hier noch weitere Beispiele zur Kettenregel an!
Ableitungen wichtiger Funktionen
Die Ableitungen einiger wichtiger Funktionen solltest du am besten auswendig lernen.
Manchmal kommen diese Funktion aber auch in komplizierter Form vor, zum Beispiel e3x + 4 oder ln(x2). Dann kannst du mit der Kettenregel die Ableitungen bilden. Dabei gehst du so vor:
Beispiel 1: f(x) = e3x + 4
- Leite die Hochzahl ab: 3x + 4 → 3
- Schreibe die e-Funktion ab und multipliziere sie mit der Ableitung der Hochzahl: e3x + 4 → e3x + 4 · 3
Und schon hast du die e-Funktion abgeleitet! Das ging dir zu schnell? Dann schau dir unseren extra Beitrag dazu an.
Beispiel 2: f(x) = ln(x2)
- Leite den Term im ln ab: x2 → 2x
- Schreibe die gesamte Ableitung hin. Sie lautet:
![Rendered by QuickLaTeX.com \[f'(x) = \frac{1}{\textcolor{teal}{\text{Term im ln}}}\cdot \textcolor{orange}{\text{Ableitung vom Term im ln}} = \frac{1}{\textcolor{teal}{x^2}}\cdot \textcolor{orange}{2x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3be5cccdd7598c510e8c8931dbe9a58c_l3.png)
Wie genau das mit der Ableitung vom Logarithmus funktioniert, erfährst du in unserem Beitrag dazu!
Ableitung — häufigste Fragen
(ausklappen)
Ableitung — häufigste Fragen
(ausklappen)-
Was sagt mir die Ableitung an einer Stelle x über den Graphen?Die Ableitung f'(x) sagt dir die Steigung des Graphen an der Stelle x. Sie entspricht der Steigung der Tangente, die den Graphen dort berührt. Setzt du einen konkreten x-Wert in f'(x) ein, bekommst du genau diese Tangentensteigung.
-
Wie erkenne ich mit der Ableitung, ob eine Funktion steigt oder fällt?Du erkennst das am Vorzeichen von f'(x): Ist f'(x) > 0, steigt die Funktion, und ist f'(x) gilt zum Beispiel: f'(-1,5) = 3,75 > 0, also steigt sie dort.
-
Was bedeutet es, wenn die erste Ableitung an einer Stelle 0 ist?Wenn f'(x) = 0 ist, hat die Funktion dort eine Extremstelle oder einen Sattelpunkt. Das passt dazu, dass die Tangente an dieser Stelle waagrecht ist. Im Beispiel f(x) =
 ist bei x = 1 f'(1) = 0, dort liegt ein Tiefpunkt.
ist bei x = 1 f'(1) = 0, dort liegt ein Tiefpunkt.
-
Wie kann ich die Ableitung zeichnen, ohne sie auszurechnen?Du zeichnest die Ableitung graphisch, indem du markante Stellen des Graphen von f(x) überträgst. Extremstellen von f(x) werden zu Nullstellen von f'(x), und Wendestellen von f(x) werden zu Extremstellen von f'(x). Danach verbindest du die Punkte zu einer Kurve.
-
Wie entsteht die Formel für die Ableitung über Sekante und Tangente?Du startest mit der Steigung einer Sekante durch zwei Punkte P(x0|y0) und Q(x|y):
 . Dann lässt du den Abstand x zu x0 gegen 0 gehen. So bekommst du
. Dann lässt du den Abstand x zu x0 gegen 0 gehen. So bekommst du  , die Tangentensteigung.
, die Tangentensteigung.
Kurvendiskussion
Ableitungen in Mathe brauchst du vor allem für die Kurvendiskussion. Dabei untersuchst du verschiedene Fragen rund um eine Funktion und findest so heraus, wie der Graph einer Funktion aussieht:
- Monotonie : Wo steigt und wo fällt die Funktion? → Wo ist die erste Ableitung positiv und wo negativ?
- Extremstellen: Wo hat der Graph einen Hochpunkt oder einen Tiefpunkt ? → Wo ist die Ableitung gleich 0?
- Krümmungsverhalten : Wo ist die Funktion rechtsgekrümmt und wo linksgekrümmt? → Das findest du mit der zweiten Ableitung heraus.
- Wendepunkte : Wo ist die Krümmung 0, also die Steigung der Funktion konstant? → Auch hierfür brauchst du die zweite Ableitung.
Du willst mehr über die Kurvendiskussion erfahren? Dann schau dir unser Video dazu an!