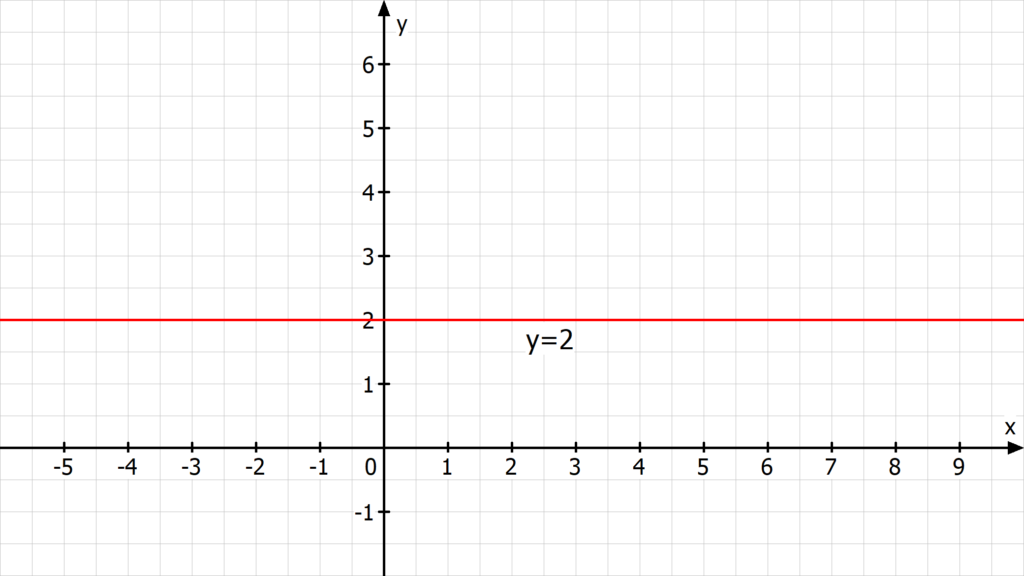
Geradengleichung
In diesem Beitrag fassen wir dir alles Wichtige zum Thema Geradengleichungen zusammen und zeigen dir, wie du sie aufstellst. Schau dir auch unser Video dazu an!
Inhaltsübersicht
Was ist eine Geradengleichung?
Eine Linie kannst du in Mathe mit einer Geradengleichung beschreiben. Die allgemeine Geradengleichung lautet:
![Rendered by QuickLaTeX.com \[y=\textcolor{red}{m} \cdot x +\textcolor{orange}{t}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-731bcc762faef36657f0e5d1259ebc1b_l3.png)
Dabei ist m die Steigung der Gerade. Du kannst sie mithilfe eines Steigungsdreiecks bestimmen. Das t ist der y-Achsenabschnitt, also der Wert, bei dem die Gerade die y-Achse schneidet.
Um die Steigung der Gerade zu bestimmen, setzt du zwei beliebige Geradenpunkte – zum Beispiel A(-1|1) und B(1|5) – in den sogenannten Differenzenquotient ein.
![Rendered by QuickLaTeX.com \[\textcolor{red}{m}= \frac { \textcolor{blue}{f(b)}-\textcolor{olive}{f(a)}} { b-\textcolor{purple}{a}} = \frac { \textcolor{blue}{5}-\textcolor{olive}{1}} { 1-\textcolor{purple}{(-1)}} =\textcolor{red}{2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-40407cc223a03e2a8708d849c47d1342_l3.png)
Du siehst, dass die Steigung m=2 und der y-Achsenabschnitt t=3 betragen. Setzt du diese Werte in die allgemeine Geradengleichung y=m·x+t ein, erhältst du
![Rendered by QuickLaTeX.com \[y=\textcolor{red}{2}x+\textcolor{orange}{3}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-16c6a1e6d302faaf6be4cb721f75b898_l3.png)
Geradengleichungen aufstellen
Willst du eine Geradengleichung aufstellen, gibt es drei mögliche Szenarien. Sie unterscheiden sich in den Informationen, die dir gegeben sind.
- Geradengleichung durch zwei Punkte bestimmen
- Geradengleichung aus einem Punkt und der Steigung bestimmen
- Geradengleichung aus y-Achsenabschnitt und einem Punkt bestimmen
Schauen wir uns das einmal genauer an!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Geradengleichung durch zwei Punkte bestimmen
Sind dir zwei Punkte gegeben, mit denen du eine Gleichung aufstellen sollst, gehst du in drei Schritten vor.
Beispiel: Du hast die Punkte A(-1|1) und B(2|3). Berechne die Gleichung der Geraden, die durch A und B verläuft.
1. Berechne die Steigung m mithilfe des Differenzenquotienten. Teile dazu die Differenz der y-Werte durch die Differenz der x-Werte von A und B.
![Rendered by QuickLaTeX.com \[\textcolor{red}{m}=\frac{\textcolor{olive}{1}-\textcolor{blue}{3}}{\textcolor{purple}{-1}-2} = \frac{-2}{-3} = \frac{2}{3} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-333495ef837631d44b63ee6bb6b50f8e_l3.png)
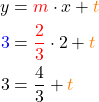
Als Nächstes berechnest du t.

![Rendered by QuickLaTeX.com \[y = \textcolor{red}{\frac{2}{3}}x +\textcolor{orange} {\frac{5}{3} }\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8e0da9170a146859591016d3ae6f25bb_l3.png)
Super, damit hast du die Aufgabe gelöst!
Geradengleichung aus einem Punkt und der Steigung bestimmen
Beispiel: Gegeben sind die Steigung m=4 und der Punkt P(-1|1). Berechne die zugehörende Geradengleichung!
1. Setze die Steigung m=4 und die Koordinaten des Punktes P(-1|1) in die allgemeine Geradengleichung y=m·x+t ein. Dadurch kannst du und den y-Achsenabschnitt t bestimmen.

Als Nächstes addierst du beide Seiten mit 4.

2. Setze die Steigung m=4 und den y-Achsenabschnitt t=5 in die allgemeine Geradengleichung y=m·x+t ein.
![Rendered by QuickLaTeX.com \[y =\textcolor{red}{4} x +\textcolor{orange}{5} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-413447904521d3f187c9a82b662d8097_l3.png)
Geradengleichung aus y-Achsenabschnitt und einem Punkt bestimmen
Beispiel: Gegeben sind der y-Achsenabschnitt t=-3 und der Punkt P(2|1) .Berechne die zugehörende Geradengleichung!
1. Setze den y-Achsenabschnitt t=-3 und die Koordinaten des Punktes P(2|1) in die allgemeine Geradengleichung y=m·x+t ein und löse nach der Steigung m auf.

2. Setze die Steigung m=2 und den y-Achsenabschnitt t=-3 in die allgemeine Geradengleichung y=m·x+t ein.
![Rendered by QuickLaTeX.com \[y = \textcolor{red}{2}x\textcolor{orange}{-3} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6aa7b8f7a353ba5aa58dd55f073c0f53_l3.png)
Um eine allgemeine Geradengleichung aufzustellen, brauchst du die Steigung und den Schnittpunkt der Gerade mit der y-Achse. Das setzt du in die Gleichung y = mx + t ein. m ist dabei die Steigung und t der Schnittpunkt.
Besondere Geraden
Manche Geraden haben eine besondere Lage im Koordinatensystem. Hier haben wir dir diese Geraden und ihre wichtigsten Eigenschaften zusammengefasst.
Die Identität
Hier siehst du die Gerade, die man Identität nennt. Ihre Gleichung ist y=x. Sie ist eine besondere Ursprungsgerade, weil sie die Steigung m=1 hat. Sie halbiert deswegen den ersten und dritten Quadranten. Da sie auch den Winkel zwischen x- und y-Achse schneidet, heißt sie auch Winkelhalbierende.
Geradengleichung — häufigste Fragen
(ausklappen)
Geradengleichung — häufigste Fragen
(ausklappen)-
Was bedeuten die Steigung m und der y-Achsenabschnitt t?Die Steigung m gibt an, wie stark die Gerade steigt oder fällt, wenn x größer wird. Der y-Achsenabschnitt t ist der y-Wert, an dem die Gerade die y-Achse schneidet. In der Form
 legt m die Neigung und t die Verschiebung nach oben oder unten fest.
legt m die Neigung und t die Verschiebung nach oben oder unten fest.
-
Wie berechne ich die Steigung aus zwei Punkten?Die Steigung m berechnest du aus zwei Punkten, indem du die Differenz der y-Werte durch die Differenz der x-Werte teilst:
 . Zum Beispiel bei
. Zum Beispiel bei  und
und  gilt
gilt  .
.
-
Wie finde ich den y-Achsenabschnitt t mit einem Punkt?Den y-Achsenabschnitt t findest du, indem du einen bekannten Punkt
 und die Steigung m in
und die Steigung m in  einsetzt und nach t umstellst. Konkret: Bei
einsetzt und nach t umstellst. Konkret: Bei  und
und  gilt
gilt  , also ist
, also ist  .
.
-
Wann kann ich eine Gerade nicht als y gleich m mal x plus t schreiben?Eine Gerade kann nicht als
 geschrieben werden, wenn sie parallel zur y-Achse verläuft. Dann wäre die Steigung unendlich und die allgemeine Geradengleichung passt nicht. Solche senkrechten Geraden haben stattdessen immer die Form
geschrieben werden, wenn sie parallel zur y-Achse verläuft. Dann wäre die Steigung unendlich und die allgemeine Geradengleichung passt nicht. Solche senkrechten Geraden haben stattdessen immer die Form  , wobei c eine feste Zahl ist.
, wobei c eine feste Zahl ist.
-
Wie erkenne ich eine Ursprungsgerade an der Gleichung?Eine Ursprungsgerade erkennst du daran, dass der y-Achsenabschnitt
 ist, also die Gleichung die Form
ist, also die Gleichung die Form  hat. Dann kann man sie auch als
hat. Dann kann man sie auch als  schreiben. Beispiel:
schreiben. Beispiel:  ist eine Ursprungsgerade, weil hier
ist eine Ursprungsgerade, weil hier  gilt.
gilt.
Schnittpunkte zweier Geraden
Nachdem du eine Geradengleichung gefunden hast, kannst du damit zum Beispiel den Schnittpunkt zweier Geraden zu berechnen. Schau dir gleich unser Video an, in dem du die Schritt für Schritt Anleitung dafür bekommst!