Dielektrizitätskonstante
In diesem Beitrag erklären wir dir das Wichtigste zum Thema Dielektrizitätskonstante. Du erfährst unter anderem, welche wichtigen Rollen sie spielt und lernst typische Werte kennen.
Du möchtest das Thema in kürzester Zeit verstehen? Dann schau dir unbedingt unser Video zur Dielektrizitätskonstante an!
Inhaltsübersicht
Dielektrizitätskonstante einfach erklärt
Im Alltag triffst du auf eine Vielzahl an unterschiedlichen Substanzen, wie etwa Metalle, Wasser oder Sauerstoff. Jede dieser Substanzen reagiert unterschiedlich auf elektrische Felder .
Die Permittivität (Dielektrizitätskonstante)  beschreibt die Polarisationsfähigkeit eines Materials durch elektrische Felder und ist gegeben durch
beschreibt die Polarisationsfähigkeit eines Materials durch elektrische Felder und ist gegeben durch
 .
.
Hier ist 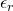 die relative Permittivität und
die relative Permittivität und  die Permittivität des Vakuums. Statt der Bezeichnung Permittivität findest du auch den Begriff Dielektrizitätskonstante.
die Permittivität des Vakuums. Statt der Bezeichnung Permittivität findest du auch den Begriff Dielektrizitätskonstante.
Nimmt man die Bedeutung des Begriffs Permittivität wörtlich, dann ist diese ein Maß dafür, wie stark Materie ein elektrisches Feld „zulässt“. Die Dielektrizitätskonstante kann also als ein Ausmaß dafür angesehen werden, wie sehr Materie sich polarisieren lässt.
Dielektrizitätskonstante des Vakuums
Die Dielektrizitätskonstante des Vakuums (auch Permittivität des Vakuums) spielt eine besondere Rolle. In diesem Abschnitt zeigen wir dir, welchen Wert und welche Einheit die Dielektrizitätskonstante des Vakuums hat, wie sie mit anderen Konstanten zusammenhängt und welche Bedeutung sie im Zusammenhang mit anderen wichtigen Gesetzen besitzt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Zahlenwert und Einheit
Die Dielektrizitätskonstante des Vakuums  besitzt den für Rechnungen praktischeren Wert von
besitzt den für Rechnungen praktischeren Wert von 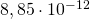 . Die Einheit der Konstante ist
. Die Einheit der Konstante ist
 .
.
Fügen wir beides zusammen und nehmen den experimentell bestimmten Wert der Dielektrizitätskonstante des Vakuums, dann erhalten wir
 .
.
Weitere Bezeichnungen für die Dielektrizitätskonstante des Vakuums sind
- Permittivität des Vakuums,
- elektrische Feldkonstante,
- elektrische Konstante oder
- Influenzkonstante.
Bis auf elektrische Feldkonstante und Permittivität des Vakuums, findest du die anderen Bezeichnungen seltener vor.
Zusammenhang mit anderen Konstanten
Zwischen der Dielektrizitätskonstante des Vakuums  , der magnetischen Feldkonstanten
, der magnetischen Feldkonstanten  und der Lichtgeschwindigkeit in Vakuum
und der Lichtgeschwindigkeit in Vakuum 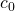 herrscht eine bemerkenswerte Beziehung. Es gilt
herrscht eine bemerkenswerte Beziehung. Es gilt
 .
.
Bis zum Jahr 2019 war mit dieser Gleichung der Wert der elektrischen Feldkonstanten exakt festgelegt. Dies hat sich jedoch bei einer Revision geändert und seit dem 20. Mai 2019 sind sowohl die elektrische Feldkonstante als auch die magnetische Feldkonstante mit einer bestimmten Messunsicherheit behaftet.
Diese Gleichung war ein erster Hinweis darauf, dass es sich bei Licht um eine elektromagnetische Welle handeln könnte. Eine wahrlich bemerkenswerte Aussage.
Coulombsches Gesetz und Elektrisches Potential
Neben der Beziehung zur Lichtgeschwindigkeit, kommt die elektrische Feldkonstante in weiteren wichtigen Gesetzen der Elektrodynamik vor. Dazu zählen zum Beispiel
 und
und
- das elektrische Potential eines geladenen Teilchens
 .
.
Insbesondere das Coulombsche Gesetz ist die Grundlage der Elektrostatik und somit besitzt auch die elektrische Feldkonstante eine große Bedeutung.
Permittivität isolierender Stoffe
In isolierenden Stoffen (Dielektrika) sind die Ladungen an Atome oder Moleküle gebunden. Sie können sich daher nur innerhalb der Atome oder Moleküle wenig bewegen. Ein elektrisches Feld kann die Ladungsverteilung eines Dielektrikums auf zwei wichtige Wege verändern: Dehnung und Rotation. Auch wenn sich die einzelnen Ladungen nur geringfügig bewegen können, bestimmt die Gesamtheit aller Bewegungen das Verhalten eines isolierenden Stoffes.
Polarisation
Je nachdem, ob das Material aus polaren oder unpolaren Molekülen besteht, ist die Reaktion auf ein äußeres elektrisches Feld anders. Bei einem unpolaren Molekül kommt es zu einer Dehnung, wodurch das Feld in jedem Molekül des Materials ein Dipolmoment
induziert. Diese Dipolmomente zeigen alle in die gleiche Richtung wie das elektrische Feld. Bei einem polaren Molekül kommt es hingegen zu einer Drehung, sodass auch hier alle Dipolmomente in Richtung des Feldes zeigen. Insgesamt bewirkt daher ein äußeres elektrisches Feld, dass innerhalb des Materials eine große Anzahl an Dipole ensteht, die alle dem äußeren Feld gleichgerichtet sind. Das Material wurde somit polarisiert. Die Polarisation  beschreibt wie viele Dipolmomente pro Einheitsvolumen es im Material gibt.
beschreibt wie viele Dipolmomente pro Einheitsvolumen es im Material gibt.
Die Polarisation eines Dielektrikums wird also durch ein elektrisches Feld verursacht. Die dadurch entstehenden gerichteten Dipolmomente erzeugen ihrerseits ein elektrisches Feld, das dem äußeren Feld entgegengerichtet ist. Dieses entgegengerichtete Feld schwächt somit das äußere Feld. Im Allgemeinen ist die Beziehung zwischen Polarisation und äußeres elektrisches Feld kompliziert. Für viele Substanzen, sogenannten linearen Dielektrika, ist die Polarisation proportional zum Feld. Es gilt
 .
.
Hier ist  die elektrische Feldkonstante und
die elektrische Feldkonstante und  die elektrische Suszeptibilität. Das elektrische Feld
die elektrische Suszeptibilität. Das elektrische Feld  in dieser Gleichung ist das gesamte Feld. Die Ursache dafür können daher zu einem Teil freie Ladungen und zum anderen Teil die Polarisation selbst sein. Unter freien Ladungen versteht man all diejenigen Ladungsträger, die nicht Folge der Polarisation sind. Dieses gesamte elektrische Feld lässt sich damit nur sehr schwer ausrechnen, da wir über die Verteilung der Polarisationsladungen in der Regel keine Information haben.
in dieser Gleichung ist das gesamte Feld. Die Ursache dafür können daher zu einem Teil freie Ladungen und zum anderen Teil die Polarisation selbst sein. Unter freien Ladungen versteht man all diejenigen Ladungsträger, die nicht Folge der Polarisation sind. Dieses gesamte elektrische Feld lässt sich damit nur sehr schwer ausrechnen, da wir über die Verteilung der Polarisationsladungen in der Regel keine Information haben.
Dielektrische Verschiebung
Um auch bei Anwesenheit eines Dielektrikum trotzdem das elektrische Feld berechnen zu können, führt man die dielektrische Verschiebung  ein. In einem linearen Medium gilt
ein. In einem linearen Medium gilt
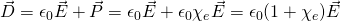
und somit ist auch  proportional zu
proportional zu  . Fasst du die Konstanten zu
. Fasst du die Konstanten zu
 ,
,
zusammen, so erhälst du
 .
.
Die Konstante  heißt Dielektrizitätskonstante (Permittivität, seltener auch dielektrische Leitfähigkeit).
heißt Dielektrizitätskonstante (Permittivität, seltener auch dielektrische Leitfähigkeit).
Relative Permittivität
Die Größe

heißt relative Permittivität (auch relative Dielektrizitätskonstante). Mit ihr gilt für das gesamte elektrische Feld in Anwesenheit eines Dielektrikums
 .
.
Bei einer konstanten dielektrischen Verschiebung bestimmt daher die relative Permittivtät wie stark das elektrische Feld geschwächt wird. Je größer die relative Permittivität ist, umso stärker wird das elektrische Feld geschwächt und somit nimmt die gesamte elektrische Feldstärke ab.
Die Bezeichnung relative Dielektrizitätskonstante kann zum Missverständnis führen, dass die relative Permittivität für ein gegebenes Material eine Konstante sei. Tatsächlich hängt die relative Permittivität von vielen Faktoren ab. Unter anderem zählen dazu
- Temperatur des Materials,
- Frequenz des äußeren elektrischen Felds und
- Feldstärke des äußeren elektrischen Felds.
Für bestimmte Materialien ist die relative Permittivität zusätzlich noch richtungsabhängig. Im Fall solcher Materialien ist sie daher nicht nur eine Zahl, sondern häufig ein Tensor zweiter Stufe.
Eine besonders anschauliche Darstellung des Einflusses von Dielektrika mit unterschiedlichen relativen Permittivitäten kannst du erhalten, wenn du zwischen zwei Kondensatorplatten
ein Dielektrikum einführst. Misst du die Spannung
am Kondensator vor und nach der Einführung des Dielektrikums, wirst du feststellen, dass sich die Spannung am Kondensator genau um den Wert 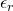 der relativen Permittivität reduziert. Das folgt direkt aus der Gleichung
der relativen Permittivität reduziert. Das folgt direkt aus der Gleichung

für den Betrag des elektrischen Feld zwischen den Platten eines Kondensators
, die sich im Abstand  zueinander befinden. Hier wird auch veranschaulicht, weswegen
zueinander befinden. Hier wird auch veranschaulicht, weswegen 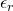 relative Permittivität heißt. Die Spannung am Kondensator wird durch Einführen eines Dielektrikums um den Faktor
relative Permittivität heißt. Die Spannung am Kondensator wird durch Einführen eines Dielektrikums um den Faktor 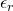 relativ zum Fall, wenn sich zwischen den Platten nur Vakuum befindet, reduziert.
relativ zum Fall, wenn sich zwischen den Platten nur Vakuum befindet, reduziert.
Dielektrizitätskonstanten ausgewählter Materialien
Zum Abschluss geben wir dir noch eine Tabelle mit typischen Werten für die relative Permittivität (relative Dielektrizitätskonstante) verschiedener Materialien. Du solltest beachten, dass in solchen Tabellen allgemein die relative Permittivität und nicht die Permittivtät selbst dargestellt wird. Wenn du also nach einer Tabelle für die Dielektrizitätskonstante eines bestimmten Materials suchst, musst du dir in Erinnerung rufen, dass der dort angegebene Wert nicht direkt die gesuchte Dielektrizitätskonstante ist. Du kannst aber für einen gegebenen Wert der relativen Dielektrizitätskonstante ohne weiteren großen Aufwand die dazugehörige Dielektrizitätskonstante berechnen. Es gilt nämlich
 .
.
| Medium | 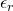 |
| Vakuum | exakt 1 |
| Helium | 1,000065 |
| Kupfererz | 5,6 |
| Luft (trocken) | 1,00059 |
| Methanol | 32,6 |
| Papier | 1 – 4 |
| Wasser (20°C, 0 – 3 GHz) | 80 |
| Wasser (0°C, 0 – 1 GHz) | 88 |
Wir hatten im vorherigen Abschnitt erwähnt, dass die relative Permittivität unter anderem von der Temperatur und Frequenz abhängig ist. Daher ist es wichtig, dass du sowohl die Temperatur als auch die Frequenz kennst, wenn du den Wert aus einer Tabelle entnehmen möchtest. Die relative Permittivität von Wasser bei 20°C und 0 GHz ist beispielsweise 80. Ist die Temperatur hingegen 0°C, die Frequenz aber dieselbe, dann ist die relative Permittivität von Wasser 88. Kupfer hingegen hat eine relative Permittivität von 5,6. Das bedeutet, dass Wasser als Medium die Spannung an einem Kondensator um den Faktor 80 reduzieren würde, während Kupfer diese nur um den Faktor 5,6 vermindert.
