Video anzeigen

Stromteiler

Wichtige Inhalte in diesem Video

Stromteiler einfach erklärt

(00:14)

Stromteiler Formel

(01:41)

Stromteiler berechnen

(00:45)

Stromteiler mit zwei Widerstandswerten

(02:48)

Stromteiler mit drei Widerständen

(03:21)

In diesem Beitrag zeigen wir dir wie du mit dem Stromteiler Schaltungen schneller analysieren kannst. Außerdem erklären wir dir hier seine Formel und demonstrieren dir seine Anwendung. Dabei betrachten sowohl den Stromteiler für zwei als auch für drei Widerstände.

Eine noch anschaulichere Erklärung mit Bild und Ton zu diesem Thema bekommst du in unserem Video .

Inhaltsübersicht

Stromteiler einfach erklärt

im Videozur Stelle im Video springen

(00:14)

Der Stromteiler ist eine Parallelschaltung elektrischer oder magnetischer elektrotechnischer Bauteile.

Merke

Die Stromteilerregel beschreibt, wie du bei gegebenem Gesamtstrom, die Teilströme einer Parallelschaltung von Widerständen berechnen kannst.

Du brauchst also nicht umständlich die Teilspannungen an den Widerständen berechnen, um aus ihnen anschließend die Teilströme zu erhalten, sondern errechnest die Teilströme direkt.

Stromteiler Formel

im Videozur Stelle im Video springen

(01:41)

Analog zum Spannungsteiler , beschreibt der Stromteiler das Verhältnis zwischen einem Teilstrom und dem Gesamtstrom einer Parallelschaltung von Widerständen.

Stromteiler, Widerstand, Parallelschaltung, Teilstrom, Gesamtstrom — Stromteiler Allgemein

Die Formel für den Teilstrom I_n lautet:

$I_n = I_{gesamt} \cdot \frac{G_n}{G_{gesamt}}$

Dabei entspricht G_n dem Leitwert des vom Teilstrom I_n durchflossenen Widerstands. $G_{gesamt}$ ist hier die Summe der Leitwerte aller Widerstände in der Parallelschaltung.

$G_n= \frac{1}{R_n} \quad \quad G_{gesamt}= \sum_{i=1}^n G_i=G_1 + G_2 + G_3+.....+G_n$

Stromteiler berechnen

im Videozur Stelle im Video springen

(00:45)

Im Folgenden wird ein einfaches Beispiel zur Anwendung des Stromteilers berechnet. Dafür ist folgende Schaltung mit der Spannungsquelle U_0 gleich 20V, R_1 gleich 50 $\Omega$ , R_2 gleich 100 $\Omega$ und R_3 gleich 40 $\Omega$ gegeben. Gesucht ist der Teilstrom I_2 durch den Widerstand R_2 .

Stromteiler, Widerstand, Parallelschaltung, Teilstrom, Gesamtstrom, Stromteiler 2 Widerstände — Stromteiler Beispiel mit 2 Widerständen

Zunächst wird dafür der Gesamtstrom $I_{gesamt}$ berechnet. Dafür teilst du die angelegte Spannung durch den gesamten Widerstand der Schaltung.

$I_{gesamt}= \frac{U_1}{R_1+R_2//R_3}= \frac{U_1}{R1+\frac{R_2 \cdot R_3}{R_2+R_3}}$

$I_{gesamt}= \frac{20V}{50\Omega+100\Omega//40\Omega}= \frac{20V}{50\Omega+\frac{100\Omega\cdot 40\Omega}{100\Omega+40\Omega}} = 255mA$

Im nächsten Schritt kannst du den berechneten Gesamtstrom nutzen, um den Teilstrom I_2 zu bestimmen. Hierfür wird die oben genannte Stromteilerformel verwendet.

$I_2 = I_{gesamt} \cdot \frac{G_2}{G_{gesamt}}$

$I_2 = I_{gesamt} \cdot \frac{\frac{1}{100\Omega}}{\frac{1}{100\Omega}+\frac{1}{40\Omega}}= 72,9mA$

Dabei gilt $G_2=\frac{1}{R_2}$ und $G_{gesamt}=\frac{1}{R_2}+\frac{1}{R_3}$ . Dabei ist wichtig, dass G_1 nicht Teil von $G_{gesamt}$ ist, da der Widerstand R1 nicht Teil der Parallelschaltung ist.

Stromteiler mit zwei Widerstandswerten

im Videozur Stelle im Video springen

(02:48)

Alternativ ist die Berechnung auch direkt über die Widerstandswerte ohne Umrechnung in Leitwerte möglich.

Die hier vorgestellte Methode gilt allerdings nur für Parallelschaltungen von zwei Widerständen. Um den Teilstrom I_2 zu erhalten, wird in diesem Fall der Gesamtstrom $I_{gesamt}$ mit dem Widerstand, der nicht vom Teilstrom durchflossen wird, multipliziert und anschließend durch die Summe der beiden Widerstände geteilt.

$I_2 = I_{gesamt} \cdot \frac{R_3}{R_2+R_3}$

Werden nun auch hier die Zahlenwerte eingesetzt, ergibt sich der Teilstrom I_2 identisch zu der allgemeinen Methode oben.

$I_2 = I_{gesamt} \cdot \frac{40\Omega}{40\Omega+100\Omega}=72.9mA$

Stromteiler mit drei Widerständen

im Videozur Stelle im Video springen

(03:21)

Für Schaltungen mit mehr als zwei Widerständen kann die Berechnung der Teilströme ebenfalls über die Stromteilerregel erfolgen. In folgendem Beispiel ist der Gesamtstrom I_1 mit 500mA gegeben.

Stromteiler, Stromteiler Beispiel, Widerstand, Teilstrom, Gesamtstrom, Stromteiler 3 Widerstände — Stromteiler mit 3 Widerständen

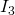Der Widerstand R_2 beträgt hier 50 $\Omega$ , R_3 gleich 100 $\Omega$ und R_4 gleich 150 $\Omega$ . Gesucht wird der Wert des Teilstroms I_3 . Mit der Berechnung über die Leitwerte ergibt sich: