Hochpass
Du hast heute auf dem Weg zur Arbeit Radio gehört? Dann hast du den Hochpassfilter heute schon benutzt, auch wenn nur unbewusst. In diesem Artikel möchten wir dir die Funktionsweise dieses Filters erklären, zeigen aus welchen einfachen Bauelementen er besteht und dir dann seine Eigenschaften wie Grenzfrequenz und Übertragungsfunktion erläutern.
Wenn du dieses Thema lieber in Videoform erklärt haben möchtest, dann schau dir doch unser Video dazu an!
Inhaltsübersicht
Hochpass einfach erklärt
Im Allgemeinen lässt ein Hochpass Spannungen mit Frequenzen über einer bestimmten Grenzfrequenz passieren. Daher kommt auch der Name Hochpassfilter. Unterhalb dieser Grenzfrequenzen werden die Spannungen blockiert. Zur Grenzfrequenz haben wir bereits ein ausführliches Video, welches du dir auch gerne ansehen kannst. Der Filter wird meistens durch einen Widerstand R und einen Kondensator C realisiert, kann aber auch aus einem Widerstand R und einer Spule L aufgebaut werden.
RC Hochpass
In diesem Artikel wird überwiegend der RC Hochpass behandelt, wie du ihn in folgender Schaltung erkennst. Du siehst, dass in diesem Fall ein Kondensator  in Reihe zu einem Widerstand
in Reihe zu einem Widerstand 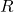 geschalten wird. An den linken Klemmen wird die Eingangsspannung
geschalten wird. An den linken Klemmen wird die Eingangsspannung  angelegt und parallel zum Widerstand kannst du die Ausgangsspannung
angelegt und parallel zum Widerstand kannst du die Ausgangsspannung  abgreifen.
abgreifen.
Hier ist ein Filter 1. Ordnung dargestellt, das heißt, dass in der Schaltung ein Kondensator und ein Widerstand vorhanden sind. Ein Filter 2. Ordnung hätte dementsprechend zwei Kondensatoren und zwei Widerstände. Darauf werden wir später noch genauer eingehen.
Um den Hochpass zu verstehen musst du wissen, dass sich der Blindwiderstand  , also der Widerstand eines Kondensators bei einer bestimmten Frequenz, mit 1 geteilt durch die Kreisfrequenz
, also der Widerstand eines Kondensators bei einer bestimmten Frequenz, mit 1 geteilt durch die Kreisfrequenz  mal Kapazität
mal Kapazität  berechnen lässt.
berechnen lässt.

Wenn an der Eingangsspannung eine sehr niedrige Frequenz  anliegt, also
anliegt, also  , so gilt für die Ausgangsspannung:
, so gilt für die Ausgangsspannung:

Die Begründung hierfür ist, dass der Blindwiderstand  für niedrige Frequenzen steigt. Der Strom sieht sozusagen einen sehr großen Widerstand und somit fällt hier ein Großteil der Spannung ab. Du kannst dir das so vorstellen, dass der Kondensator die Schaltung unterbricht. Das hat zur Folge, dass keine Ausgangsspannung
für niedrige Frequenzen steigt. Der Strom sieht sozusagen einen sehr großen Widerstand und somit fällt hier ein Großteil der Spannung ab. Du kannst dir das so vorstellen, dass der Kondensator die Schaltung unterbricht. Das hat zur Folge, dass keine Ausgangsspannung  abfällt.
abfällt.
Liegt jedoch am Eingang eine hohe Frequenz an, so erhältst du:

Das kannst du so verstehen, dass für  der Blindwiderstand
der Blindwiderstand  gegen 0 geht. Hier kann der Strom also fast ungehindert hindurch. Der Kondensator kann als Kurzschluss angenommen werden, was zur Folge hat, dass fast die komplette Eingangsspannung am Ausgang anliegt.
gegen 0 geht. Hier kann der Strom also fast ungehindert hindurch. Der Kondensator kann als Kurzschluss angenommen werden, was zur Folge hat, dass fast die komplette Eingangsspannung am Ausgang anliegt.
Schau dir unser Video über den Tiefpassfilter an, falls du noch weiter in die Thematik einsteigen möchtest.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Hochpass Bodediagramm
Was genau das Bodediagramm zeigt, haben wir bereits in einem anderen Artikel erklärt. In unserem Fall lässt sich sagen, dass dieses Diagramm den Frequenzverlauf eines Hochpassfilters beschreibt.
Beachte, dass die Frequenz logarithmisch eingetragen ist!
Im Amplitudengang siehst du bei der typischen Verstärkung von -3dB, oder einem Verhältnis der Amplituden von  , die Grenzfrequenz
, die Grenzfrequenz  . Oberhalb dieser Frequenz beginnt der Filter die Spannung durchzulassen.
. Oberhalb dieser Frequenz beginnt der Filter die Spannung durchzulassen.
Nach der Grenzfrequenz nähert sich die Kurve relativ schnell der Verstärkung von 0dB, beziehungsweise dem Verhältnis von 1. Das bedeutet einfach, dass  gilt.
gilt.
Im Bodediagramm kannst du auf Anhieb erkennen, ab welcher Frequenz der Filter die Spannung blockt (Sperrbereich), beziehungsweise die Spannung durchlässt (Durchlassbereich).
Hochpass Grenzfrequenz
Zum Thema Grenzfrequenz haben wir bereits ein eigenes Video. Willst du mehr darüber erfahren, dann schaue es dir unbedingt an!
Zusammengefasst ist die Grenzfrequenz  die Frequenz, bei der sich der Widerstand R und Blindwiderstand
die Frequenz, bei der sich der Widerstand R und Blindwiderstand  abgleichen, also:
abgleichen, also:

Wir haben ja bereits dargestellt, wie sich der Blindwiderstand berechnen lässt.

Aus

ergibt sich nun durch umformen nach der Grenzfrequenz die Formel:

Im Phasengang wird der Phasenwinkel  der Schaltung über der Frequenz aufgetragen. Bei der Grenzfrequenz siehst du einen Winkel
der Schaltung über der Frequenz aufgetragen. Bei der Grenzfrequenz siehst du einen Winkel  von genau
von genau  °. Das lässt sich auch ganz einfach erklären. Wir haben vorher gesagt, dass bei der Grenzfrequenz
°. Das lässt sich auch ganz einfach erklären. Wir haben vorher gesagt, dass bei der Grenzfrequenz  gilt. Setzt du das in folgende Formel für den Phasenwinkel ein, erhälst du:
gilt. Setzt du das in folgende Formel für den Phasenwinkel ein, erhälst du:
 °
°
Hochpass Übertragungsfunktion
Da ein Hochpassfilter ein dynamisches System ist, lässt sich hierfür eine Übertragungsfunktion bilden.
Zum Thema Übertragungsfunktionen haben wir ebenfalls ein ausführliches Video, in dem alle wichtigen Aspekte detailliert erklärt werden.
Um die Übertragungsfunktion herzuleiten stellt man den Spannungsteiler auf, welcher das Verhältnis von Eingangsspannung  zu Ausgangsspannung
zu Ausgangsspannung  beschreibt. Daraus folgt:
beschreibt. Daraus folgt:

Wenn du nun den Bruch mit  erweiterst
erweiterst

und  einsetzt erhältst du die Hochpass Übertragungsfunktion
einsetzt erhältst du die Hochpass Übertragungsfunktion
 .
.
Du kannst dir nun nochmal die Grenzwerte mithilfe dieser Funktion deutlich machen.
Für  gilt
gilt

und für  gilt
gilt
 .
.
Das bedeutet, dass für Frequenzen gegen Null das Verhältnis von Ein- und Ausgangsspannung Null ist. Das ist so, da 1 geteilt durch  gegen Null geht. Für Frequenz gegen unendlich wird das Verhältnis Eins.
gegen Null geht. Für Frequenz gegen unendlich wird das Verhältnis Eins.
RL Hochpass
Im RL Hochpass kommt statt einem Kondensator eine Spule zum Einsatz, die folgendermaßen verschalten werden.
Dieser Filter hat zwar die selbe Wirkung wie der RC Hochpass, verhält sich aber anders, da nun die Ausgangsspannung parallel zur Spule abgegriffen wird.
Die Spule L hat den Blindwiderstand  .
.

Wir können jetzt wieder ähnliche Überlegungen wie vorher anstellen.
Für  geht der Blindwiderstand
geht der Blindwiderstand  gegen 0. Der Strom sieht so gut wie kein Hindernis, somit fällt auch keine Spannung an der Spule ab. Daraus folgt:
gegen 0. Der Strom sieht so gut wie kein Hindernis, somit fällt auch keine Spannung an der Spule ab. Daraus folgt:

Zum besseren Verständnis kannst du dir vorstellen, als wäre die Spule bei niedrigen Frequenzen nur ein normaler Draht, also ein Kurzschluss.
Für  wird der Blindwiderstand
wird der Blindwiderstand  sehr groß. Der Großteil der Spannung wird an der Spule abfallen, die sozusagen eine Unterbrechung erzeugt. Somit erhält man:
sehr groß. Der Großteil der Spannung wird an der Spule abfallen, die sozusagen eine Unterbrechung erzeugt. Somit erhält man:

Das Ergebnis unserer Überlegung ist nun, dass niedrige Frequenzen von der Schaltung geblockt werden. Für hohe Frequenzen ist die Ausgangsspannung gleich der Eingangsspannung, sie lässt also die Spannung passieren. Daraus können wir schlussfolgern, dass die Schaltung ebenfalls ein Hochpassfilter ist.
Hochpass 2. Ordnung
Bis jetzt haben wir Hochpassfilter 1. Ordnung behandelt. Für einen Hochpass 2. Ordnung werden einfach zwei Filter 1. Ordnung in Reihe geschalten.
Wenn du wieder die Grenzfrequenz bestimmst erhältst du folgende Formel:

Im Bodediagramm hat ein Hochpassfilter 2. Ordnung (Blau) eine Steigung von 40dB/Dekade. Du kannst auch sagen, dass dieser doppelt so steil ist wie ein Hochpass 1. Ordnung (Rot). Somit hat ein Filter höherer Ordnung einen schärferen Übergang zwischen Sperr- und Durchlassbereich.



