Video anzeigen

Induktivität

Wichtige Inhalte in diesem Video

Was ist Induktivität?

(00:18)

Induktionsspannung ermitteln

Was ist die Induktivität und wo kannst du sie vorfinden? Alles Wichtige findest du hier und im Video dazu!

Inhaltsübersicht

Was ist Induktivität?

im Videozur Stelle im Video springen

(00:18)

Die Induktivität ist eine physikalische Größe, welche bei einem elektrischen Leiter die Fähigkeit zur Selbstinduktion beschreibt. Somit drückt sie aus, wie gut der elektrische Leiter bei Veränderung des Stromflusses ein Magnetfeld aufbauen und in Form von magnetischer Feldenergie speichern kann.

Du kannst sie mit folgender Formel berechnen:

$L = \frac{N \cdot \phi}{I}$

Jede der Buchstaben steht hierbei für eine andere Variable:

L: Induktivität
N: Windungszahl des elektrischen Leiters
Φ (Phi): Magnetischer Fluss

Ein typisches Beispiel für einen Leiter mit hoher Induktivität ist die Spule. Die vielen Windungen der Spule erhöhen nämlich die Stärke des Magnetfelds, weshalb auch die Induktivität steigt.

Induktivität — Einheit und Formelzeichen

Die Induktivität hat als Formelzeichen ein L. Sie wird in der Einheit mit dem Buchstaben H (Henry) angegeben.

In Formelsammlungen siehst du deshalb auch manchmal folgende Kurzschreibweise:

$\lbrack L \rbrack = 1 \, \rm{H} \, \text{(Henry)}$

1 Henry entspricht dabei einer Spannungsänderung von 1 Volt, wenn sich der Strom im Leiter um 1 Ampere pro Sekunde ändert.

Induktionsspannung ermitteln

im Videozur Stelle im Video springen

(00:26)

In Leitern entsteht eine Induktionsspannung, wenn Strom durch sie fließt. Mithilfe der Induktivität kannst du ermitteln, wie hoch die entstehende Induktionsspannung im elektrischen Bauteil sein wird. Dafür benutzt du folgende Formel:

$U_{\text{ind}} = L \cdot \dot I = L \cdot \hspace{-0,75cm} \underbrace{\frac{\text{d}I}{\text{d}t}}_\text{Stromänderung}$

Induktivität berechnen

Wenn du die Induktivität eines elektrischen Leiters berechnen willst, eignet sich die allgemeine Formel:

$L = \frac{N \cdot \phi}{I}$

Wenn du jetzt allerdings für spezielle Leiter die Induktivität herausfinden möchtest, kommen andere Variationen der Formel zum Einsatz. Diese berücksichtigen beispielsweise die geometrische Form oder das Kernmaterial der Spule.

Zylinderspule

im Videozur Stelle im Video springen

(04:48)

Die Zylinderspule ist eine röhrenförmige Spule, welche aus einem spiralförmig umwickelten Kern besteht.

induktivität, induktivität spule, zylinderspule — Zylinderspule

Die Induktivität einer Zylinderspule kannst du mit folgender Formel berechnen:

$L = N^2 \cdot \frac{\mu_\rm{r} \mu_\rm{0} A }{l}$

Jeder Buchstabe wird entweder einer Größe oder einer Konstanten zugeordnet:

Buchstabe	Größe oder Konstante
L	Induktivität
N	Windungszahl der Zylinderspule
µ_r	Permeabilität bzw. die Durchlässigkeit für Magnetfelder
µ₀	Magnetische Feldkonstante (µ₀ ≈ 1,257 ⋅ 10^-6 N/A²)
A	Querschnittfläche der Spule

Aufgrund der Zylinderform kannst du für die Fläche der Spule die Formel für eine Kreisfläche verwenden:

$A = \pi r^{2}$

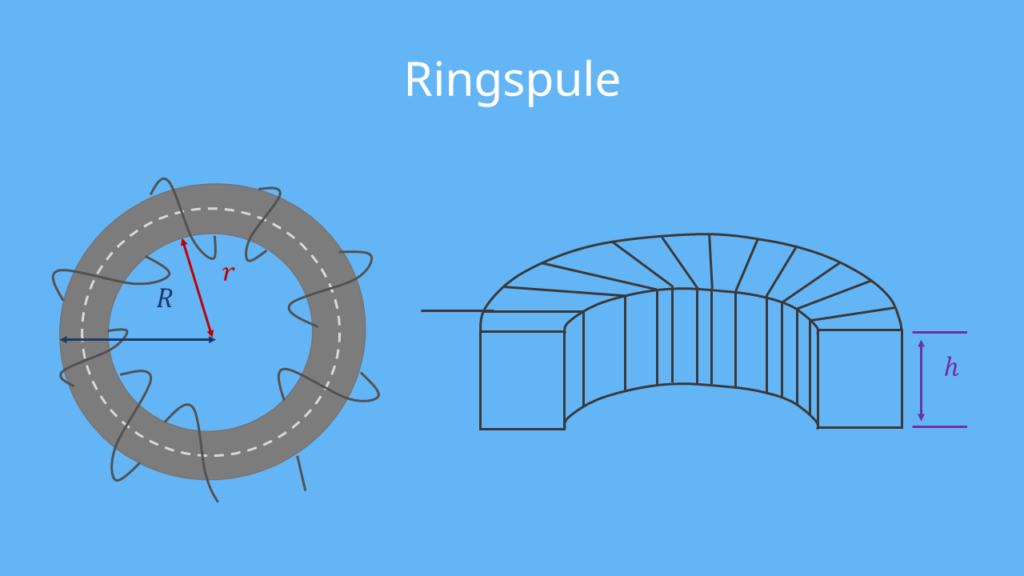
Ringspule

im Videozur Stelle im Video springen

(05:04)

Die Ringspule ist eine ringförmige Spule, die auch manchmal Toroidspule genannt wird.

induktivität, induktivität spule, ringspule — Ringspule

Die Induktivität einer Ringspule kannst du mit folgender Formel berechnen:

$L = N^2 \cdot \frac{\mu_r \cdot \mu_0 \cdot h }{2 \pi} \cdot \ln(\frac{R}{r})$

Die Variablen in dieser Formel sind ganz ähnlich zu denen der Zylinderspule:

Buchstabe	Größe oder Konstante
L	Induktivität
N	Windungszahl der Ringspule
µ_r	Permeabilität bzw. die Durchlässigkeit für Magnetfelder
µ₀	Magnetische Feldkonstante (µ₀ ≈ 1,257 ⋅ 10^-6 N/A²)
h	Höhe der Spule
R	Äußerer Radius
r	Innerer Radius

Induktivität messen

Die Induktivität einer Spule kann auf verschiedene Arten gemessen werden.

Eine Methode zur Messung besteht darin, Stromänderungen in der Spule in Abhängigkeit von der angelegten Spannung zu messen. Hierzu kann ein Oszilloskop verwendet werden. Durch Betrachtung der zeitlichen Verschiebung zwischen dem Strom und der Spannung kann die Induktivität berechnet werden.

Darüber hinaus kann zur Messung ein LCR-Meter verwendet werden. LCR-Meter sind Geräte, welche die Induktivität, Kapazität und den Widerstand von elektronischen Bauteilen messen können. Um die Induktivität einer Spule mit einem LCR-Meter zu ermittelt, wird die Spule einfach an das Messgerät angeschlossen und der Wert wird automatisch berechnet.

Eine weitere Methode zur Messung ist die Verwendung eines Schwingkreises . Ein Schwingkreis besteht aus einer Spule und einem Kondensator. Durch Messung der Resonanzfrequenz des Schwingkreises kann die Induktivität der Spule berechnet werden.

Induktivität — häufigste Fragen

Was ist Induktivität?
Die Induktivität ist eine physikalische Größe, welche die Fähigkeit zum Aufbau und Speicherung eines Magnetfeldes bei elektrischen Leitern ausdrückt.
Wie lautet die Induktivität Formel?
Die Induktivität Formel für eine lange Spule lautet: L = μ0 ⋅ (N² ⋅A) / l . Mit dem Ergebnis dieser Formel kann dann die Spulenenergie berechnet werden: W_L=
Wie kann man die Induktivität messen?
Die Induktivität einer Spule kann durch Messung der Stromänderung in der Spule in Abhängigkeit von der angelegten Spannung bestimmt werden. Dies kann mit einem Oszilloskop oder einem LCR-Meter erfolgen. Alternativ kann die Induktivität auch durch Messung der Resonanzfrequenz in einem Schwingkreis mit einer Spule berechnet werden.

Selbstinduktion — Ein- und Ausschaltvorgang

Die Induktivität spielt eine große Rolle beim Ein- und Ausschaltvorgang eines Stromkreises mit einer Lampe und einer Spule, die in Reihe geschaltet sind.

Sowohl beim Ein- als auch beim Ausschaltvorgang bremst die Induktivität der Spule nämlich den Stromfluss. Das führt dazu, dass die Lampe erst allmählich angeht und später beim Ausschalten auch lediglich langsam verglüht.

Das ist ein Effekt der Selbstinduktion. Wie dieses Phänomen genau abläuft, erfährst du in diesem Video dazu!