Elektrische Energie
Was ist elektrische Energie und wo wird sie verwendet? Alles Wichtige dazu findest du hier im Beitrag und in unserem Video heraus!
Inhaltsübersicht
Was ist elektrische Energie?
Die elektrische Energie ist eine Energieform, die durch elektrischen Strom transportiert wird. Sie kann dazu verwendet werden, Objekte in Bewegung zu setzen, Wärme zu erzeugen oder Licht auszusenden. Zwei Anwendungsmöglichkeiten sind zum Beispiel das Drehen eines Ventilators oder das Licht einer Glühbirne.
Die elektrische Energie kannst du mit folgender Formel berechnen:
Eel = U ⋅ I ⋅ t
Hierbei steht jeder Buchstabe für etwas anderes:
- Eel: Elektrische Energie
- t: Zeit
- U: Spannung
- I: Stromstärke
Die Energie ist somit immer größer, wenn entweder Zeit, Spannung oder Stromstärke ansteigen.
Elektrische Energie ist die Energie, die in elektrischen Feldern und Magnetfeldern vorliegt. Sie ist in der Lage, elektrische Ladungen zu bewegen. Dadurch funktionieren Geräte und Elektronik wie Lampen oder Computer. Sie ist eine wichtige Energiequelle für viele Aspekte des modernen Lebens.
Elektrische Energie Einheit und Formelzeichen
Die elektrische Energie besitzt als Formelzeichen E, wobei die elektrische Energie Einheit Wattsekunde (Ws) ist. Dabei stellt Joule (J) die eigentliche Standard-Einheit für jede Energieform dar. Mit dieser Vereinheitlichung ist auch zwischen verschiedenen Ländern klar, dass du bei Joule von der Energie sprichst.
1 Joule ist dabei die vorhandene Energie, wenn eine Spannung von 1 Volt für 1 Sekunde bei einem Widerstand von 1 Ohm aufrechterhalten wird und dabei ein Strom mit der Stromstärke 1 Ampere fließt.
In Formelsammlungen siehst du für die elektrische Energie auch manchmal diese Kurzschreibweise:
[ E ] = 1 J
Elektrische Energie Formel
Die allgemeine elektrische Energie Formel lautet folgendermaßen:
![\[E_{\rm{el}} = U \cdot I \cdot t \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8a3435bb209d299e3216f39f3f223a37_l3.png "Rendered by QuickLaTeX.com")
Beim besonderen Fall eines Kondensators mit einer Kapazität C kann die Energie im elektrischen Feld zwischen den Platten gespeichert werden. Die elektrische Energie Formel für die gespeicherte Energie sieht dann wie folgt aus:
![\[E_{\rm{el}} = \frac{1}{2} \cdot C \cdot U^2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6a840f7649bece2f5536f51f341004f1_l3.png "Rendered by QuickLaTeX.com")
Wenn eine Ladung bewegt wird, wird elektrische Energie aufgewendet. Du sprichst dann von elektrischer Arbeit. Sie wird mit dieser Formel berechnet:
![\[W_{\rm{el}} = U \cdot Q\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f3aedd951bf47c26a34b4a666486b050_l3.png "Rendered by QuickLaTeX.com")
Ein Kondensator besteht aus zwei Metallplatten, die sich gegenüberstehen. Zwischen diesen kann eine Spannung aufgebaut werden, sodass sich der Kondensator auflädt. Ein Beispiel für einen Kondensator ist ein Defibrillator.
Elektrische Energie Beispiele
Elektrische Energie ist ein wichtiger Bestandteil unseres täglichen Lebens. Sie ermöglicht es uns, elektrische Geräte zu betreiben.
Zum Beispiel wird die elektrische Energie genutzt, um die Lampen in unseren Häusern und Straßen zum Leuchten zu bringen. Auch Küchengeräte wie Toaster und Mikrowellen benötigen elektrische Energie, um zu funktionieren.
Weitere elektrische Energie Beispiele sind:
- Heizungen
- Motoren
- Elektrische Werkzeuge wie Bohrmaschinen
- Telefone und Computer
- Kühlschrank
- Fernseher
- Solarzellen
- Stromkraftwerke
Elektrische Energie — Vergleich zur Gravitation
Die elektrische Energie ist in der Lage, elektrische Ladungen zu bewegen. Deswegen macht es Sinn, sie mit der Lageenergie bzw. potenziellen Energie bei Massen zu vergleichen.
Beim Fall einer Masse aus einer Höhe h verwendest du für die potenzielle Energie folgende Formel:
![\[E_{\rm{pot}} = m \cdot g \cdot h\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fe7e209d2d15a06b9408d69be35b6a4a_l3.png "Rendered by QuickLaTeX.com")
Hier steht m für die Masse und g für die Erdbeschleunigung. Für den Vergleich zur elektrischen Energie fassen wir g ⋅ h mit Ug zusammen. Das heißt:
![\[U_g = g \cdot h \: \widehat{=} \: \textbf{"Potenzial"} \right\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-360680ddb55c612940ee38ca37ffb8dc_l3.png "Rendered by QuickLaTeX.com")
Damit lautet die potenzielle Energie:
![\[E_{\rm{pot}} = m \cdot U_g\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3ac3694a40c07d20a6430bae5321f13f_l3.png "Rendered by QuickLaTeX.com")
Die Formel für elektrische Energie erhältst du, wenn du nun das m mit der elektrischen Ladung q und Ug mit der Spannung U ersetzt.
![\[E_{\rm{el}} = q \cdot U\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eb99ef1408cfedffafd6d23fcab5bb20_l3.png "Rendered by QuickLaTeX.com")
Die Spannung bezeichnet nichts anderes als das elektrische Potenzial zwischen zwei Ladungen. Also ist die elektrische Energie eine potenzielle Energie bei Ladungen.
In der folgenden Tabelle siehst du den Vergleich auf einen Blick:
| Feld | Größe | Potenzielle Energie | Einheit des „Potenzials“ |
| Gravitation |  |
[ ] = 
|
| Elektrisch |  |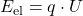
[ ] = 
|
Gut zu wissen: Eine Besonderheit bei der Elektrizität ist, dass es negative und positive Ladungen gibt. Sie bestimmen die Richtung der Anziehung. Bei der Gravitation existiert nichts Vergleichbares. Masse zieht ausschließlich an und hat keine Ladungen.
Die Lageenergie ist die Energie, die ein Objekt aufgrund seiner Höhe hat. Zum Beispiel hat ein Ball auf einem Regal eine Lageenergie. Die kann zur Bewegungsenergie umgewandelt werden, wenn er fällt.
Elektrische Energie — häufigste Fragen
-
Was ist die elektrische Energie Formel?
Die elektrische Energie Formel ist dieselbe wie für die elektrische Arbeit. Somit lautet die elektrische Energie Formel: Wel = U ⋅ I ⋅ t. Die Einheit der elektrischen Arbeit ist: [Wel] = 1 V ⋅ A s = 1 Ws (Wattsekunde) = 1 J (Joule).
-
Was ist der Unterschied zwischen der elektrischen Energie und der elektrischen Arbeit?
Die elektrische Arbeit beschreibt die Änderung der elektrischen Energie. Somit bezeichnet die Arbeit einen Prozess, während die Energie einen Zustand in einem elektrischen oder magnetischen Feld beschreibt. Die elektrische Arbeit lässt sich mit folgender Formel berechnen: Wel = U ⋅ I ⋅ t.
-
Was ist die elektrische Energie Einheit?
Die elektrische Energie Einheit ist Joule (J). Für die Berechnung der elektrischen Energie werden drei Werte miteinander multipliziert. Darunter ist die Stromstärke mit der Einheit Ampere (A) und dem Formelzeichen I, die Spannung mit der Einheit Volt (V) und dem Formelzeichen U und die Zeit mit der Einheit Sekunde (s) und dem Formelzeichen t.
Plattenkondensator
Wenn ein Plattenkondensator unter Spannung gesetzt wird, liegt in seinem elektrischen Feld auch elektrische Energie vor. Was ein Plattenkondensator genau ist, erfährst du in diesem Video dazu!
