Elektromagnetische Induktion und Induktionsspule
In diesem Beitrag definieren wir die elektromagnetische Induktion, erklären die Induktionsspule, stellen die Formel für die Induktionsspannung auf und zeigen dir die Drei-Finger-Regel.
In unserem Video dazu findest du alles wichtige zum Thema nochmal auf einen Blick.
Inhaltsübersicht
Elektromagnetische Induktion einfach erklärt
Die elektromagnetische Induktion beschreibt das Phänomen der Entstehung einer elektrischen Spannung an einem elektrischen Leiter durch ein sich veränderndes Magnetfeld.
Du kannst dir also merken, dass wenn du einen elektrischen Leiter (zum Beispiel eine Leiterschleife) in ein veränderliches Magnetfeld bringst, an ihr eine Spannung abfallen wird. Diese Spannung wird als Induktionsspannung bezeichnet.
Stromdurchflossener Leiter: Leiterschleife und Induktionsspule
Hier siehst du einen stromdurchflossenen geraden Leiter. An jedem Punkt des Leiters erzeugt der Strom ein Magnetfeld, das kreisförmig um den Leiter verläuft. Das Feld ist dabei auf einer Ebene, die senkrecht zum Leiter liegt.
Insgesamt kann man sich das Magnetfeld also wie eine zylindrische Ummantelung des Leiters vorstellen. Die Rechte Hand Regel hilft dir, die Richtung der Feldlinien zu bestimmen.
Krümmt man den Leiter nun zu einer Schleife, dann krümmt man auch diese Ummantelung. Ein Querschnitt durch das magnetische Feld sieht so aus:
Eine übliche Induktionsspule besteht aber nicht aus einer einzigen Schleife, sondern aus vielen Wicklungen. Hier siehst du das Magnetfeld einer Induktionsspule mit 4 Schleifen.
Wenn also eine induzierte Spannung in einer Spule festgestellt wird, wird sie auch als Induktionsspule bezeichnet. Dieses Magnetfeld der Induktionsspule bringt uns nun näher an die elektromagnetische Induktion.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Leiterschleife im Magnetfeld
Machen wir nun ein Experiment. Dazu brauchen wir einen Leiter, z.B. ein Stück Draht und einen Magneten, der ein magnetisches Feld erzeugt.
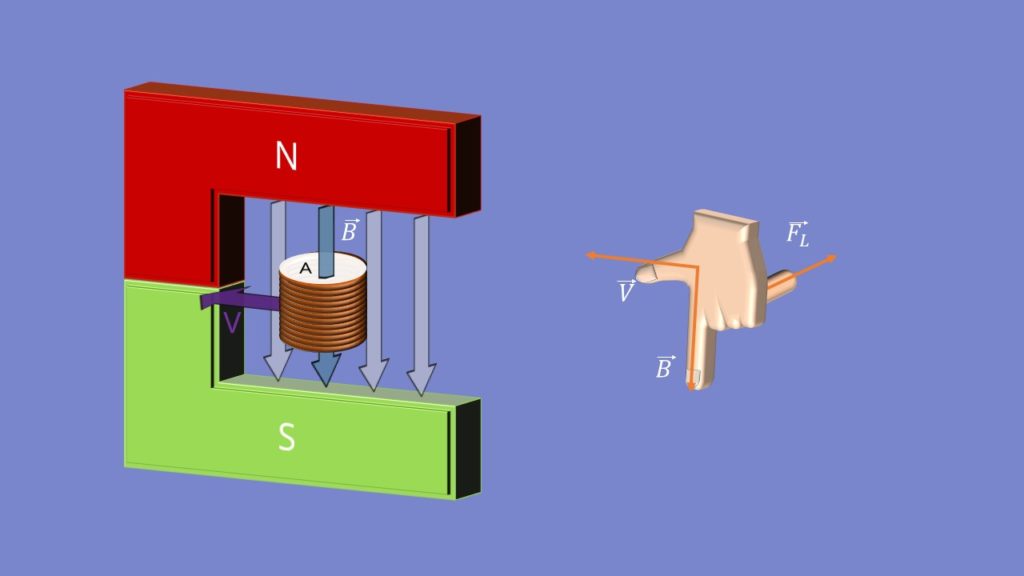
Bewegt man nun den Leiter senkrecht zu den Feldlinien des Magnetfelds , so wirkt auf die Ladungen innerhalb des Leiters eine Kraft. Diese Kraft wird auch als Lorentzkraft bezeichnet.
Dadurch werden die Ladungsträger senkrecht zum Magnetfeld und senkrecht zur Bewegungsrichtung des Leiters abgelenkt, sodass in unserem Beispiel am hinteren Drahtende ein Überschuss an Elektronen entsteht und das vordere Drahtende positiv geladen ist.
Die Ladungstrennung bewirkt das Auftreten einer elektrischen Kraft. Sie wirkt entgegengesetzt zur Lorentzkraft. Bei Bewegung des Leiters mit konstanter Geschwindigkeit halten sich die Lorentzkraft und die elektrische Kraft auf eine Ladung in Waage.
Diese Ladungsträgertrennung erzeugt die Induktionsspannung Uind. Die Spannung berechnen wir für den Fall, dass sich keine Elektronen mehr bewegen, da sich die Lorentzkraft und die elektrische Feldkraft gegenseitig aufheben.
Induktionsspannung berechnen
Im Folgenden erklären wir dir die Herleitung zur Berechnung der Induktionsspannung.
Wie bereits erwähnt führt die Lorentzkraft zu einer Ladungsträgertrennung, die wiederum ein elektrisches Feld mit der Kraft  erzeugt. Die beiden kompensieren sich gegenseitig und sind daher betragsmäßig gleich groß. Es gilt daher:
erzeugt. Die beiden kompensieren sich gegenseitig und sind daher betragsmäßig gleich groß. Es gilt daher:

Die Lorentzkraft ist dabei gleich der magnetischen Feldstärke B mal der Ladung q mal der Geschwindigkeit v, mit der das Drahtstück ins Feld hinein bewegt wird. Die elektrische Feldkraft ist die elektrische Feldstärke E mal die Ladung q. 
Die Ladung q kannst du jetzt wegkürzen. E ersetzt du mit U durch die Drahtlänge d. Dabei ist U die Induktionsspannung und somit unsere gesuchte Größe.

Die Induktionsspannung berechnen wir indem wir nach ihr auflösen. Die Induktionsspannung wird also erzeugt, wenn ein Leiter der Länge d mit der Geschwindigkeit v in ein Magnetfeld mit der Stärke B gebracht wird.

Elektromagnetische Induktion und Linke Hand Regel
Jetzt schauen wir uns die Teilchenbewegung der Elektronen genauer an.
Zur Bestimmung der Richtungen nehmen wir wieder die Drei-Finger-Regel der linken Hand. Der Daumen ist dann die Bewegungsrichtung des Leiters, der Zeigefinger gibt die Richtung des B-Feldes an und der Mittelfinger ist die Lorentzkraft.
Um die elektromagnetische Induktion ganz zu verstehen, tauschen wir unser kurzes Leiterstück gegen eine Induktionsspule mit N Windungen und der Fläche A.
Zudem brauchen wir eine neue Größe: den magnetischen Fluss Φ . Wir kennen bereits die magnetische Flussdichte B, die die Dichte der Feldlinien pro Fläche A beschreibt. Demnach ist der magnetische Fluss:

In unserem Beispiel haben wir jetzt aber eine Induktionsspule mit N Windungen, also N Leiterschleifen der Fläche A. Daher müssen wir die Formel anpassen, indem noch ein N dazukommt. Die Formel lautet damit:

Das Magnetfeld durchläuft die Fläche A der Leiterschleife senkrecht. Immer dann, wenn sich der magnetische Fluss ändert, der die Fläche A durchsetzt, entsteht ein Induktionsspannungsstoß. Dies führt uns zu der Erkenntnis, dass die Ursache der Änderung des magnetischen Fluss Φ ist unwichtig. Sie kann sowohl auf einer Bewegung des Leiters oder einer Änderung des magnetischen Feldes beruhen.
Elektromagnetische Induktion von Spannung
Die erste Möglichkeit für die elektromagnetische Induktion einer Spannung beschreibt folgende Formel:

Wichtig ist dabei, dass  nur die vom Feld durchdrungene Fläche der Leiterschleife ist und B senkrecht durch A geht.
nur die vom Feld durchdrungene Fläche der Leiterschleife ist und B senkrecht durch A geht.
Die Formel zeigt auch, dass die induzierte Spannung und somit auch deren Höhe von der Geschwindigkeit v abhängt, mit der die Leiterschleife ins Feld hineinbewegt wird.
Bei schneller Bewegung ergibt sich eine hohe Induktionsspannung während einer kurzen Zeit und bei langsamer Bewegung eine kleinere Induktionsspannung während einer längeren Zeitdauer. Die Fläche unter der Kurve ist aber in beiden Fällen gleich groß.
Sobald unsere Leiterschleife komplett im Magnetfeld des Hufeisenmagnetes liegt, lässt sich trotz weiterer Hinein-Bewegung keine Induktionsspannung mehr messen. Zum Zeitpunkt t1 beziehungsweise t2 befindet sich der Leiter vollständig im Magnetfeld.
Das Magnetfeld innerhalb des Hufeisenmagnetes ist homogen. Für eine elektromagnetische Induktion muss es eine Änderung des magnetischen Flusses geben. Dazu müssen wir die Leiterschleife also aus dem Hufeisenmagnet raus oder in ihn hinein bewegen! Nicht die Bewegung an sich, sondern die Veränderung der vom felddurchdrungenen Fläche erzeugt die elektromagnetische Induktion.
Eine zweite Möglichkeit für die elektromagnetische Induktion von Spannung ist eine Veränderung des magnetischen Feldes. Dann gilt die Gleichung:
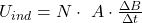 .
.
Das Magnetfeld eines Hufeisenmagnetes können wir jetzt nicht so einfach verändern, dazu bräuchten wir nämlich jedes Mal einen neuen Magneten.
Allgemein gilt: Spulen erzeugen Magnetfelder. Tauschen wir unseren Permanentmagnet doch einfach durch eine Induktionsspule aus und variieren ihren Strom. Dadurch entsteht in ihrem Inneren ein zeitlich veränderliches Magnetfeld.
Zusammenfassung
Eine Induktionsspule der Länge L mit W Wicklungen erzeugt in ihrem Inneren ein Magnetfeld B. Es gilt:

Wie du an der Formel erkennen kannst, kann man das Magnetfeld mit Variation des Stromes I verändern.
Eine Leiterschleife mit N Windungen umschließt die Fläche A. Hier hat die Leiterschleife nur eine Windung. Innerhalb der Fläche A liegen Feldlinien des Magnetfeldes.
Das Spannungsmessgerät misst eine Induktionsspannung infolge der Änderung des magnetischen Flusses. Wenn der Strom in der Induktionsspule konstant bleibt, messen wir nichts.
Ein Elektroauto kann zum Beispiel ohne Benzin fahren, weil im Motor die Kraft, die von einem Magnetfeld auf die stromdurchflossenen Leiter einer Induktionsspule ausgeübt wird, in Bewegung umgesetzt wird.
Induktionsgesetz
Nun kennst du die Induktion als die Entstehung einer elektrischen Spannung an einem elektrischen Leiter durch ein sich veränderndes Magnetfeld. Beschrieben wird die Induktion durch das sogenannte Induktionsgesetz. Dieses vereint den magnetischen Fluss  mit der Induktionsspannung
mit der Induktionsspannung  .
.
Wenn du wissen willst, wie das Induktionsgesetz aussieht und wie du es am Beispiel einer Leiterschleife anwenden kannst, dann schau dir gerne unseren Beitrag dazu an!