y Achsenabschnitt berechnen
In diesem Artikel erklären wir dir, was der y Achsenabschnitt ist und wie du ihn für verschiedene Arten von Funktionen berechnest. Möchtest du das Thema in kurzer Zeit erklärt bekommen? Dann schau dir unser Video dazu an!
Inhaltsübersicht
y Achsenabschnitt einfach erklärt
Manchmal wird nach dem Schnittpunkt des Funktionsgraphen mit den Achsen gefragt. Dabei wird der Schnittpunkt mit der y Achse als y Achsenabschnitt oder Ordinatenabschnitt bezeichnet.
Das Besondere am y-Achsenabschnitt ist, dass die x-Koordinate immer 0 ist!
Für eine beliebige Funktion f(x) entspricht der y Achsenabschnitt

Um den y Achsenabschnitt einer Funktion f zu berechnen, setzt du also einfach 0 in die Funktion f ein.
Beispiel: Die Funktion  hat den y Achsenabschnitt bei
hat den y Achsenabschnitt bei  .
.
y Achsenabschnitt berechnen: Lineare Funktionen
Bei linearen Funktionen
 liegt der y Achsenabschnitt immer bei
liegt der y Achsenabschnitt immer bei

Aber was machst du, wenn du den y Achsenabschnitt einer Geraden berechnen sollst, wenn du nur zwei Punkte gegeben hast, die auf der Geraden liegen?
Sind  und
und  zwei Punkte der linearen Funktion
zwei Punkte der linearen Funktion
 , so kannst du die x-Werte beider Punkte in die Funktion einsetzen. Du erhältst dann
, so kannst du die x-Werte beider Punkte in die Funktion einsetzen. Du erhältst dann


Stellst du nun beide Gleichungen nach m um, bekommst du

Nun kannst du die Gleichung nach  umstellen und erhältst somit den y Achsenabschnitt
umstellen und erhältst somit den y Achsenabschnitt

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel 1
Nehmen wir an, du hast die Punkte  und
und  einer linearen Funktion
einer linearen Funktion  gegeben. Setzt du die x-Werte der Punkte in die Funktion ein, erhältst du
gegeben. Setzt du die x-Werte der Punkte in die Funktion ein, erhältst du


Nun stellst du beide Gleichungen nach m um. Dabei bekommst du

Jetzt kannst du die Gleichung nach  umstellen und du erhältst mit
umstellen und du erhältst mit

den Schnittpunkt der Funktion mit der y Achse .
Beispiel 2
Hast du nun die lineare Funktion  gegeben, so lässt sich der Ordinatenabschnitt berechnen, indem du
gegeben, so lässt sich der Ordinatenabschnitt berechnen, indem du  einsetzt
einsetzt

y Achsenabschnitt berechnen: Ganzrationale Funktionen
Ganzrationale Funktionen sind Funktionen der Form

Willst du von Polynomfunktionen den Ordinatenabschnitt berechnen, so musst du  in die Funktion einsetzen
in die Funktion einsetzen

Das heißt, der Ordinatenabschnitt einer Polynomfunktion ist das konstante Glied  den du direkt aus der Funktionsgleichung ablesen kannst.
den du direkt aus der Funktionsgleichung ablesen kannst.
Hinweis: Das gilt natürlich auch für quadratische Funktionen , denn quadratische Funktionen sind Polynomfunktionen vom Grad 2.
y Achsenabschnitt berechnen: Gebrochenrationale Funktionen
Bei einer gebrochenrationalen Funktion
musst du nichts Besonderes beachten. In dem Fall musst du einfach  in die Funktion einsetzen.
in die Funktion einsetzen.
Beispiel
Betrachte die Funktion

Setzt du  in die Funktion ein, so erhältst du als y Achsenabschnitt
in die Funktion ein, so erhältst du als y Achsenabschnitt

Achtung: Eine gebrochenrationale Funktion  muss nicht unbedingt einen Schnittpunkt mit der y Achse haben. Ist der Nenner
muss nicht unbedingt einen Schnittpunkt mit der y Achse haben. Ist der Nenner  für
für  , dann ist die Funktion für
, dann ist die Funktion für  nicht definiert und hat somit keinen y-Achsenabschnitt.
nicht definiert und hat somit keinen y-Achsenabschnitt.
y Achsenabschnitt berechnen: Exponentialfunktionen
Exponentialfunktionen sind Abbildungen der Form

Setzt du x = 0 in f ein, so erhältst du


Der Ordinatenabschnitt einer Exponentialfunktion ist somit der Parameter a, den du auch direkt aus der Funktionsgleichung ablesen kannst.
Hinweis: Wenn du  setzt, dann hast du eine e Funktion
. Hier gilt das Gleiche.
setzt, dann hast du eine e Funktion
. Hier gilt das Gleiche.
Beispiel
Wenn du die Funktion  betrachtest, dann siehst du, dass
betrachtest, dann siehst du, dass

der Schnittpunkt mit der y Achse ist.
y Achsenabschnitt berechnen: ln-Funktionen
Bei der ln Funktion
musst du ein bisschen aufpassen. Denn die Definitionsmenge
des natürlichen Logarithmus ist ![Rendered by QuickLaTeX.com D = ]0; \infty [](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-54eddac7976c4da76a58cebfe9a0bd18_l3.png) und somit ist
und somit ist  für
für  nicht definiert und hat deshalb auch keinen y-Achsenabschnitt.
nicht definiert und hat deshalb auch keinen y-Achsenabschnitt.
Ist aber die ln Funktion mit einer anderen Funktion verschachtelt, so ist es möglich, dass die Funktion einen Schnittpunkt mit der y Achse hat.
Beispiel
Du hast folgende Funktion gegeben

Setzt du  ein, erhältst du
ein, erhältst du

und somit den y-Achsenabschnitt der Funktion.
Wichtige Begriffe der Kurvendiskussion
Bevor wir uns den Aufgaben widmen, geben wir dir an dieser Stelle eine kleine Übersicht wichtiger Begriffe, die du im Zusammenhang mit der Kurvendiskussion beherrschen solltest:
- Kurvendiskussion
- Kurvendiskussion Aufgaben
- Ableitung
- Ableitungsregeln
- Extrempunkte berechnen
- Hoch- und Tiefpunkte
- Sattelpunkt berechnen
- Monotonie
- Wendepunkt berechnen
- Wendetangente
- Symmetrie
- Punktsymmetrie
- Achsensymmetrie
y Achsenabschnitt berechnen: Aufgaben
Widmen wir uns nun ein paar Aufgaben, um das Thema besser zu verstehen.
Aufgabe 1: Ablesen des y Achsenabschnitts
Gib den y Achsenabschnitt der folgenden Funktionen an, ohne  einzusetzen.
einzusetzen.
a) 
b) 
c) 
d) 
e) 
f) 
Lösung: Aufgabe 1
a) Hier handelt es sich bei einer linearen Funktion, bei der du den y-Achsenabschnitt direkt ablesen kannst. Du schaust dir dabei an, welcher der Summanden konstant ist.
In dem Fall ist es 
b) In dem Fall kannst du den Ordinatenabschnitt nicht direkt ablesen. Dafür musst du den Term erst umschreiben

Nun hast du eine quadratische Funktion gegeben bei der du den Schnittpunkt mit der y Achse  direkt ablesen kannst.
direkt ablesen kannst.
c) Die Funktion ist eine ganzrationale Funktion, das heißt du kannst den y Achsenabschnitt  einfach ablesen.
einfach ablesen.
d) Diesmal kannst du den Ordinatenabschnitt nicht direkt sehen, denn dafür musst du den Term erstmal ausmultiplizieren. Damit ergibt sich

Nun kannst du den y Achsenabschnitt  direkt ablesen.
direkt ablesen.
e) Hier hast du eine Exponentialfunktion gegeben bei der du den y Achsenabschnitt  schnell ablesen kannst.
schnell ablesen kannst.
f) Nachdem du die Funktion in die ganzrationale Funktion

umgeformt hast, siehst du sofort den Ordinatenabschnitt 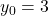 .
.
Aufgabe 2: y-Achsenabschnitt berechnen
Berechne den y Achsenabschnitt der folgenden Funktionen.
a) 
b) 
Lösung Aufgabe 2
a) Setze den Wert  in die Funktion f ein und erhalte
in die Funktion f ein und erhalte

als Schnittpunkt der Funktion mit der y Achse.
b) Wenn du  in die Funktion einsetzt, erhältst du
in die Funktion einsetzt, erhältst du

und somit den Ordinatenabschnitt der Funktion.
Schnittpunkt mit der y-Achse – kurz & knapp
Merk dir: An den Punkten, an denen deine Funktion f(x) die y-Achse schneidet, ist x = 0.
Deswegen gehst du in zwei Schritten vor, wenn du den Schnittpunkt mit der y-Achse berechnen möchtest:
- Berechne y = f(0).
- Gib die Koordinaten des Schnittpunkts an: S(0 | y).
x Achsenabschnitt
Im Gegensatz zum y Achsenabschnitt, können bestimmte Funktionen auch einen oder mehrere Schnittpunkte mit der x Achse haben. Du berechnest den x Achsenabschnitt, indem du die Funktion  setzt und die Nullstellen berechnest. Damit du die Schnittpunkte mit den Koordinatenachsen problemlos bestimmen kannst, schau dir jetzt unbedingt unser Video
zur Nullstellenberechnung an. Los gehts!
setzt und die Nullstellen berechnest. Damit du die Schnittpunkte mit den Koordinatenachsen problemlos bestimmen kannst, schau dir jetzt unbedingt unser Video
zur Nullstellenberechnung an. Los gehts!


 gegeben, so setzt du
gegeben, so setzt du 

