Tangens
Du möchtest wissen, was es mit der trigonometrischen Funktion Tangens auf sich hat? Dann bist du hier genau richtig! In unserem Beitrag und Video erfährst du alles, was du wissen musst!
Tangens einfach erklärt
Der Tangens kann dir im rechtwinkligen Dreieck dabei helfen, fehlende Seiten und Winkel zu bestimmen.
Der Tangens des Winkels α entspricht dem Verhältnis von Gegenkathete zu Ankathete:
![\[ \tan(\textcolor{red}{\alpha})=\frac{\textcolor{olive}{\text{Gegenkathete a}}}{\textcolor{purple}{\text{Ankathete b}}} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-273513be03925bac041bb9764917ac63_l3.png "Rendered by QuickLaTeX.com")
In einem rechtwinkligen Dreieck heißt die lange Seite gegenüber vom rechten Winkel Hypotenuse c . Die Ankathete b ist die Seite, die an dem gesuchten Winkel α liegt. Die Gegenkathete a ist die Seite, die dem gesuchten Winkel α gegenüberliegt.
Verwendest du außerdem die Beziehungen Sinus und Cosinus , erkennst du, dass gilt:
denn:
![\[ \frac{\sin(\alpha)}{\cos(\alpha)} = \frac{\frac{\text{Gegenkathete}}{\text{Hypotenuse}}}{\frac{\text{Ankathete}}{\text{Hypotenuse}}} =\frac{\text{Gegenkathete}}{\text{Ankathete}} = \tan(\alpha) \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2c45d5ef10099ba7360e226d7f143eb8_l3.png "Rendered by QuickLaTeX.com")
Tangens Einheitskreis
Den tan x kannst du auch am Einheitskreis darstellen. Das ist ein Kreis mit dem Koordinatenursprung als Mittelpunkt und dem Radius 1.
Dazu wählst du zuerst einen beliebigen Punkt P auf dem Einheitskreis und verbindest ihn mit dem Koordinatenursprung. Den Winkel, den die x-Achse und deine gezogene Linie einschließen, nennst du α.
Jetzt möchtest du den Wert herausfinden, den der Tangens für diesen Winkel hat. Wenn du von deinem Punkt P eine senkrechte Linie zur x-Achse zeichnest, erhälst du ein rechtwinkliges Dreieck. Zur Verdeutlichung kannst du es auch mit den Begriffen Gegenkathete und Ankathete beschriften.
Für die Berechnung des Tangens verwendest du die Formel: 
Du kannst die genauen Längen der beiden Seiten nicht richtig erkennen, also wendest du einen Trick an: Du verschiebst die Gegenkathete bis zur x-Koordinate 1. Dadurch wird sie zur Tangente vom Einheitskreis, d.h. sie berührt sie an einem Punkt.
Du darfst das übrigens wegen des Strahlensatzes machen. Dadurch ändert sich das Verhältnis von Gegenkathete und Ankathete nicht.
Jetzt kannst du den tan x einfach ablesen. Der Tangens von α ist die y-Koordinate des Punktes P‘.
Tangens Graph
Der Graph der Tangensfunktion sieht übrigens so aus:
Wir haben dir die wichtigsten Eigenschaften vom Tangens Graph zusammengefasst:
- Er hat dieselben Nullstellen wie der Sinus (…,-3π, –2π, –π, 0, π, 2π, 3π,…)
- Die Definitionslücken vom Tangens sind die Nullstellen des Cosinus (…,
π, −2π, 2π, 
π, ... ) - Es gibt keine Extrema
- Der Tangens Graph ist punktsymmetrisch
Tangens berechnen
Möchtest du etwas mit dem Tangens berechnen, gibt es einige Werte, die du dir merken kannst. Wir haben sie dir in dieser Tangenstabelle zusammengefasst:
 |
0° | 30° | 45° | 60° | 90° | 120° | 150° | 180° |
 |
0 |  |
1 |  |
nicht definiert |  |
 |
0 |
Die Werte über 180° kannst du auch ganz einfach berechnen, denn sie wiederholen sich: tan(α + 180°) = tan(α + π) = tan α
Du kannst die Winkel natürlich auch im Bogenmaß angeben. Wenn du wissen willst, wie das geht, schau dir unser Video zur Umrechnung von Gradmaß in Bogenmaß an!
Die Tangens-Wertetabelle für das Bogenmaß sieht so aus:
|
0 |  |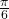
 |
 |
 |
 |
 |
 |
|
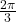0 | |
1 | |
nicht definiert | |
|
0 |
Jetzt zeigen wir dir, wie du damit die Maße eines rechtwinkligen Dreiecks berechnen kannst.
Beispiel:
Du hast ein rechtwinkliges Dreieck mit dem Winkel α = 30° und der Ankathete = 6 cm. Berechne die Länge der Gegenkathete.
Um die Aufgabe zu lösen, zeichnest du dir am besten zuerst das Dreieck auf.
Nun kannst du die Tangensformel verwenden, um die Länge der Gegenkathete zu berechnen.
Stelle die Gleichung nach der Gegenkathete um. Dazu rechnest du auf beiden Seiten mal die Ankathete.
Jetzt kannst du deine Werte einsetzen.
Deine Gegenkathete ist 
lang.
Sinus und Cosinus
Neben der Tangensfunktion gibt es in der Trigonometrie zum Beispiel noch die Funktionen Sinus, Cosinus und Cotangens . Wenn du mehr zu diesen trigonometrischen Funktionen wissen willst, schau dir unsere Videos dazu an!
