Grenzwertsätze
Du willst wissen, was die Grenzwertsätze sind und wozu du sie verwenden kannst? Dann bist du hier genau richtig. In diesem Beitrag und im Video zeigen wir dir alles Wichtige.
Inhaltsübersicht
Grenzwertsätze einfach erklärt
Die Grenzwertsätze sind Rechenregeln für die Grenzwerte von Zahlenfolgen
und Funktionen
. Mit ihnen kannst du komplizierte Terme vereinfachen und die Grenzwerte schnell berechnen. Zum Beispiel ist damit der Grenzwert von Folgen wie  gar kein Problem mehr!
gar kein Problem mehr!
Du hast zwei konvergente Folgen
(an) und (bn) mit  und
und  . Dabei ist
. Dabei ist  . Dann gilt:
. Dann gilt:

Grenzwerte berechnen Beispiel
Mithilfe der Grenzwertsätze lassen sich vermeintlich komplizierte Grenzwerte ganz einfach berechnen. Hier einige Beispiele:
An den mit * markierten Stellen wenden wir einen Grenzwertsatz an.
![Rendered by QuickLaTeX.com \begin{align*} &\lim\limits_{n\rightarrow\infty}\frac{5+3n}{n} = \lim\limits_{n\rightarrow\infty}(\textcolor{blue}{\frac{5}{n}}+\textcolor{orange}{3}) =^* \lim\limits_{n\rightarrow\infty}\textcolor{blue}{\frac{5}{n}} + \lim\limits_{n\rightarrow\infty} \textcolor{orange}{3} = 0 + 3 = 3\\ &\lim\limits_{n\rightarrow\infty}\frac{n^2-10n}{n^2}=\lim\limits_{n\rightarrow\infty}(\textcolor{blue}{1}-\textcolor{orange}{\frac{10}{n}}) =^* \lim\limits_{n\rightarrow\infty} \textcolor{blue}{1} - \lim\limits_{n\rightarrow\infty} \textcolor{orange}{\frac{10}{n}} = 1-0=1\\ &\lim\limits_{n\rightarrow\infty}\frac{\textcolor{blue}{3-\sqrt[n]{7}}}{\textcolor{orange}{1+\frac{5}{n}}} =^* \frac{\lim\limits_{n\rightarrow\infty}\textcolor{blue}{3-\sqrt[n]{7}}}{\lim\limits_{n\rightarrow\infty}\textcolor{orange}{1+\frac{5}{n}}} =^* \frac{\textcolor{blue}{3}-\lim\limits_{n\rightarrow\infty}\textcolor{blue}{\sqrt[n]{7}}}{\textcolor{orange}{1}+\lim\limits_{n\rightarrow\infty}\textcolor{orange}{\frac{5}{n}}} = \frac{3-1}{1+0}=2\\ &\lim\limits_{n\rightarrow\infty}\frac{n^3+4n+1}{3n^3+n^2}=\lim\limits_{n\rightarrow\infty}\frac{\cancel{n^3}\textcolor{blue}{(1+\frac{4}{n^2}+\frac{1}{n^3})}}{\cancel{n^3}\textcolor{orange}{(3+\frac{1}{n})}}=^*\frac{\lim\limits_{n\rightarrow\infty}\textcolor{blue}{1}+\lim\limits_{n\rightarrow\infty}\textcolor{blue}{\frac{4}{n^2}}+\lim\limits_{n\rightarrow\infty}\textcolor{blue}{\frac{1}{n^3}}}{\lim\limits_{n\rightarrow\infty}\textcolor{orange}{3}+\lim\limits_{n\rightarrow\infty}\textcolor{orange}{\frac{1}{n}}}=\frac{1}{3} \end{align*}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a8c27ae924bb245c58a9599528a7cffe_l3.png)
Achtung: Bei den markierten mit * Gleichheitszeichen musst du aufpassen. Nur wenn alle Grenzwerte auf der rechten Seite vom Gleichheitszeichen existieren (also kleiner als unendlich sind), darfst du die Sätze auch wirklich anwenden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Grenzwertsätze Beweis
Damit du die Grenzwertsätze nicht einfach blind glauben musst, findest du hier alle Beweise der Grenzwertsätze:
Beweis von (1)
Da (an) und (bn) konvergieren, wissen wir, dass für alle  zwei Zahlen
zwei Zahlen  existieren, für die gilt
existieren, für die gilt  für alle
für alle  und
und  für alle
für alle  .
.
Sei  , dann gilt für alle
, dann gilt für alle 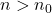 nach der Dreiecksungleichung
:
nach der Dreiecksungleichung
:
![Rendered by QuickLaTeX.com \[|\textcolor{blue}{a_n}+\textcolor{orange}{b_n}-(\textcolor{blue}{a}+\textcolor{orange}{b})|&=|(\textcolor{blue}{a_n}-\textcolor{blue}{a})+(\textcolor{orange}{b_n}-\textcolor{orange}{b})|\leq|(\textcolor{blue}{a_n}-\textcolor{blue}{a})|+|\textcolor{orange}{b_n}-\textcolor{orange}{b}|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-54d816efb632db3a37c056d56d9d4902_l3.png)
Damit haben wir gezeigt, dass  gegen a+b konvergiert.
gegen a+b konvergiert.
Beweis von (2)
Folgt aus (1) und (3), denn  .
.
Beweis von (3)
Da  konvergent ist, wissen wir, dass es ein
konvergent ist, wissen wir, dass es ein  gibt mit
gibt mit  für alle
für alle  . Daraus folgt mit der Dreiecksungleichung
. Daraus folgt mit der Dreiecksungleichung  .
.
Wähle ein beliebiges  und
und  so, dass
so, dass  und
und  für alle
für alle 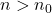 .
.
Wir müssen zeigen, dass  für alle
für alle 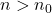 . Dafür formen wir den Term zunächst um:
. Dafür formen wir den Term zunächst um:
![Rendered by QuickLaTeX.com \[|\textcolor{blue}{a_n}\textcolor{orange}{b_n}-\textcolor{blue}{a}\textcolor{orange}{b}| = |\textcolor{blue}{a_n}\textcolor{orange}{b_n} - \textcolor{blue}{a}\textcolor{orange}{b_n} + \textcolor{blue}{a}\textcolor{orange}{b_n} - \textcolor{blue}{a}\textcolor{orange}{b}| = |\textcolor{orange}{b_n}(\textcolor{blue}{a_n}-\textcolor{blue}{a}) + \textcolor{blue}{a}(\textcolor{orange}{b_n}-\textcolor{orange}{b})|\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fbb195a1bdfe622cb37f67c5288b426b_l3.png)
Jetzt kommt wieder die Dreiecksungleichung ins Spiel, mit der wir folgende Abschätzung erhalten:

Beweis von (4)
Wir zeigen hier nur noch, dass  (Alles Weitere folgt direkt aus (3), denn
(Alles Weitere folgt direkt aus (3), denn  ).
).
Dazu betrachten wir den Term  . Wählen wir
. Wählen wir  so, dass
so, dass 
 . Aus der umgekehrten Dreiecksungleichung
folgt dann:
. Aus der umgekehrten Dreiecksungleichung
folgt dann:
![Rendered by QuickLaTeX.com \[|\textcolor{orange}{b_n}|=|\textcolor{orange}{b}-(\textcolor{orange}{b}-\textcolor{orange}{b_n})|\geq||\textcolor{orange}{b}|-|\textcolor{orange}{b_n}-\textcolor{orange}{b}||\geq |\textcolor{orange}{b}|-|\textcolor{orange}{b_n}-\textcolor{orange}{b}|>|\textcolor{orange}{b}|-\frac{|\textcolor{orange}{b}|}{2}=\frac{|\textcolor{orange}{b}|}{2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-86d83df054471691ec2df88d4affe8bd_l3.png)
Jetzt können wir für ein beliebiges  ,
,  so wählen, dass
so wählen, dass  für alle
für alle 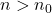 . Dann folgt:
. Dann folgt:
![Rendered by QuickLaTeX.com \[|\frac{\textcolor{orange}{b}-\textcolor{orange}{b_n}}{\textcolor{orange}{b_n}\textcolor{orange}{b}}|=\frac{|\textcolor{orange}{b_n}-\textcolor{orange}{b}|}{|\textcolor{orange}{b_n}||\textcolor{orange}{b}|}<\frac{\varepsilon\cdot\frac{2}{\textcolor{orange}{b}^2}}{|\frac{\textcolor{orange}{b}}{2}|\cdot|\textcolor{orange}{b}|}=\varepsilon\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-450dae49fa1e546b4f5ade7b6791ce3b_l3.png)
Beweis von (5)
Das ist ein direktes Ergebnis der umgekehrten Dreiecksungleichung, denn  .
.
Grenzwertsätze für Funktionen
Auch für die Grenzwerte von Funktionen lassen sich Grenzwertsätze definieren.
Sei 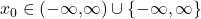 , und betrachte zwei Funktionen
, und betrachte zwei Funktionen  und
und  mit
mit  und
und  . Dabei ist
. Dabei ist  . Dann gilt:
. Dann gilt:

Dreiecksungleichung
Du weißt jetzt, was die Grenzwertsätze sind und wie man mit ihnen rechnen kann. Aber bei den Beweisen bist du immer wieder über die Dreiecksungleichung gestolpert und fühlst dich damit noch nicht ganz fit? Dann schau dir hier unser Video dazu an.
