Video

Quiz

Hier geht's zum Video „Fibonacci-Folge“

Folgen Mathe

Wichtige Inhalte in diesem Video

Was ist eine Folge in Mathematik?

Explizite und rekursive Folgen

Folgen Mathe — Grenzwert

Folgen Mathe — Monotonie

Folgen Mathe — Beschränktheit

Stehst du vor der Herausforderung, Folgen in Mathe zu verstehen? Hier im Beitrag und im Video erklären wir dir, wie sie funktionieren und was sie besonders macht!

Inhaltsübersicht

Was ist eine Folge in Mathematik?

im Videozur Stelle im Video springen

Eine Folge $(a_n)_{n\in\mathbb{N}}$ in der Mathematik ist eine Liste von Zahlen, die du Folgenglieder nennst. Jedes Folgenglied hat eine feste Position, das durch den Index „n“ angegeben wird. Die Position gibt dir dabei an, das wievielte Element in der Folge du betrachtest.

Ein einfaches Beispiel ist die Folge $a_n = 2 \cdot n$ . Hier wird jeder natürlichen Zahl „n“ ihr Doppeltes zugeordnet. Somit sind die ersten Glieder der Folge 2, 4, 6, 8 und so weiter.

Merke

Mathematisch ausgedrückt ist eine Folge eine Funktion, die jeder natürlichen Zahl n eine reelle Zahl (a_n) zuordnet.

Endliche und unendliche Folgen

Je nach Anzahl der Folgenglieder unterscheidest du zwischen endlichen und unendlichen Folgen. Eine unendliche Folge setzt sich, wie der Name schon sagt, endlos fort.

Ein Beispiel dafür ist die Folge a_n = n . Hier sind die ersten Glieder: $a_1 = 1, a_2 = 2, a_3 = 3, \ldots$ und so weiter.

Im Gegensatz dazu hat eine endliche Folge eine bestimmte Anzahl von Gliedern. Wenn du also die Definitionsmenge auf eine bestimmte Anzahl von natürlichen Zahlen begrenzt, erhältst du eine endliche Folge: a_n = n für $n \in \{1, 2, 3, 4, 5\}$ .

Hier ist das Endglied der Folge a_5 = 5 . Danach folgen keine weiteren Glieder.

Explizite und rekursive Folgen

im Videozur Stelle im Video springen

In der Mathematik gibt es zwei Arten von Bildungsvorschriften für Folgen: explizit und rekursiv. Sie beschreiben, wie du aus den ersten Folgengliedern die nächsten ableitest.

Bei einer expliziten Folge ist das Bildungsgesetz so gestaltet, dass du jedes Folgenglied direkt berechnen kannst, ohne die vorherigen Glieder zu kennen. Ein Beispiel ist die Folge: a_n = n^2

Bei einer rekursiven Folge wird jedes Folgenglied aus einem oder mehreren vorherigen Gliedern berechnet. Du kannst also ein neues Glied nicht berechnen, ohne die vorherigen zu kennen. Ein bekanntes Beispiel ist die Fibonacci-Folge, die folgendermaßen definiert ist: $a_n = a_{n-1} + a_{n-2}$

In der Fibonacci-Folge ist jedes Glied die Summe der beiden vorangegangenen Glieder: a_1 = 1, a_2 = 1, a_3 = 2, a_4 = 3, ...

Bildung rekursive & explizite Folge

Für jede Folge lässt sich eine rekursive Bildungsvorschrift angeben. Das ist immer möglich, da du jedes Folgenglied als Funktion der vorhergehenden Folgenglieder darstellen kannst.

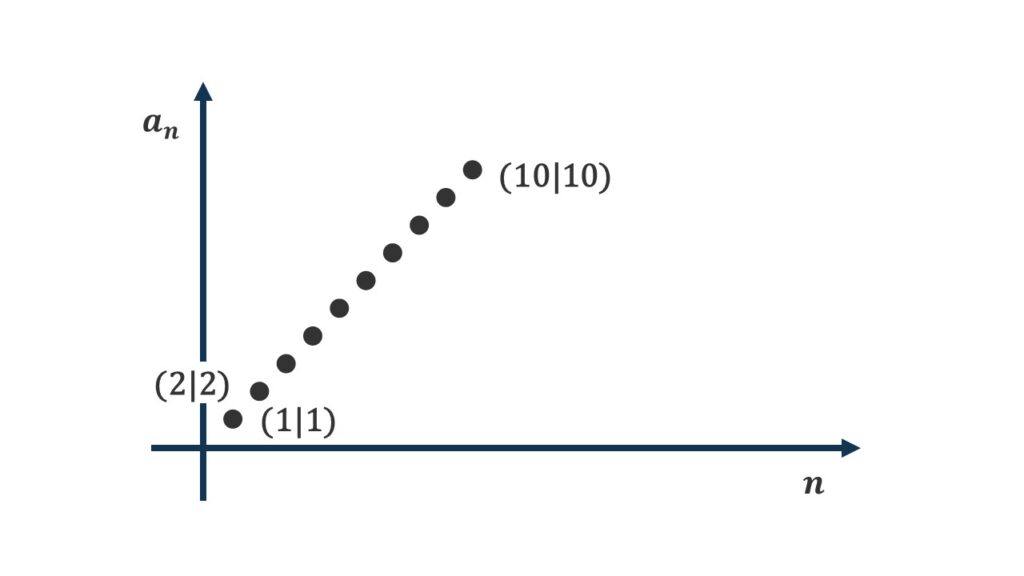
Schauen wir uns als Beispiel die Folge der natürlichen Zahlen an: $a_n = 1, 2, 3, 4, \ldots$ Alle Folgenglieder unterscheiden sich um den Wert 1. Deshalb kannst du die rekursive Bildungsvorschrift so angeben: $a_n = a_{n-1} + 1$ . Das n-te Folgenglied ist also die Summe aus dem vorherigen Folgenglied und 1.

Eine explizite Bildungsvorschrift kannst du aber nicht für jede Folge angeben. Explizite Bildungsvorschriften lassen sich nur für Folgen angeben, die einen eindeutigen Zusammenhang zwischen dem Index n und dem Folgenglied (a_n) aufweisen. Beispielsweise ist die explizite Bildungsvorschrift der Folge der natürlichen Zahlen: a_n = n . Das n-te Folgenglied der Folge ist also einfach die Zahl n.

Gut zu wissen: Für die Fibonacci-Folge oder die Folge der Primzahlen gibt es keine explizite Bildungsvorschrift.

Folgen Mathe — Grenzwert

im Videozur Stelle im Video springen

In der Mathematik betrachten wir bei Folgen oft ihre Grenzwerte. Der Grenzwert einer Folge beschreibt, was mit den Folgengliedern passiert, wenn du unendlich weit in der Folge fortschreitest. Mathematisch wird der Grenzwert einer Folge a_n als $\lim_{n \to \infty} a_n$ geschrieben.

Je nachdem, ob eine Folge einen Grenzwert besitzt, unterscheidest du zwischen zwei Begriffen:

Konvergenz
Eine Folge konvergiert, wenn sich ihre Glieder immer mehr einem bestimmten Wert annähern, ohne ihn notwendigerweise zu erreichen. Beispielsweise konvergiert die Folge $a_n = \frac{1}{n}$ gegen den Grenzwert 0, denn je größer n wird, desto näher kommt $\frac{1}{n}$ an 0 heran.

folgen, folgen mathe, folgen mathematik, folge, mathe folgen, was ist eine folge mathe, mathematik folgen, mathematische folgen, mathematische folge, folgen und reihen, folgen berechnen, folge berechnen, folgen und reihen mathe — Konvergenz

Übrigens: Folgen mit dem Grenzwert 0 bezeichnest du als Nullfolgen.

Divergenz
Eine Folge divergiert, wenn sie keinen solchen Grenzwert hat. Zum Beispiel divergiert die Folge , da sie unendlich weiter ansteigt und sich keinem festen Wert annähert.

direkt ins Video springen

Divergenz

Hier ist eine Tabelle mit einigen besonderen Grenzwerten von Folgen:

Folge	Grenzwert
$a_n = \frac{1}{n}$	0
	nicht vorhanden
$a_n = \frac{n}{n+1}$	1
$a_n = \frac{1}{2^n}$	0
$a_n = \left(1 + \frac{1}{n}\right)^n$	$\mathrm{e}$
für a > 1	$\infty$
für 0 < a < 1	0
$a_n = \sqrt[n]{a}$ für a > 0	1

Wichtig: Die eulersche Zahl $\mathrm{e}$ ist eine fundamentale Konstante in der Mathematik. Sie ist ungefähr gleich 2,71828.

Folgen Mathe — Monotonie

im Videozur Stelle im Video springen

In der Mathematik beschreibt die Monotonie einer Folge, wie sich die Folgenglieder verhalten — ob sie immer größer, immer kleiner oder gleich bleiben.

Eine Folge ist monoton wachsend, wenn jedes Glied mindestens so groß wie das vorherige ist: $a_{n+1} \geq a_n$ . Ein Beispiel ist , hier wird jedes folgende Glied größer: $a_1 = 1, a_2 = 2, a_3 = 3, \ldots$ .
Eine Folge ist monoton fallend, wenn jedes Glied höchstens so groß wie das vorherige ist: $a_{n+1} \leq a_n$ . Zum Beispiel $a_n = \frac{1}{n}$ , hier wird jedes folgende Glied kleiner: $a_1 = 1, a_2 = 0,5, a_3 = 0,33\ldots$ .
Eine Folge ist konstant, wenn jedes Glied gleich ist, also $a_{n+1} = a_n$ für alle n. Das bedeutet, dass sich die Werte der Folgenglieder nicht ändern. Ein Beispiel ist die Folge , bei der jedes Glied den Wert 5 hat, also $a_1 = 5, a_2 = 5, a_3 = 5, \ldots$ .

Monotonie bestimmen

Um die Monotonie einer Folge zu bestimmen, hast du verschiedene Möglichkeiten:

Betrachtung der Differenzen:
Wenn die Differenzen der Folgenglieder immer positiv sind, dann ist die Folge monoton wachsend:

$a_{n+1} - a_n > 0$

Wenn die Differenzen der Folgenglieder immer negativ sind, dann ist die Folge monoton fallend:

$a_{n+1} - a_n < 0$

Induktion:
Du kannst die Monotonie der Folge auch induktiv beweisen. Dafür gehst du wie folgt vor:

Induktionsanfang: Zum Beispiel möchtest du beweisen, dass die Folge monoton wachsend ist. Beim Induktionsanfang zeigst du, ob die Folge für den kleinsten Wert n= 1 monoton steigend ist. Du prüfst also, ob $a_2 \geq a_1$ ist → . Da $4 \geq 2$ , ist die Bedingung für den Induktionsanfang erfüllt. Die Folge ist also für n = 1 monoton steigend.
Induktionsschritt: Jetzt nimmst du an, dass deine Behauptung für ein beliebiges k wahr ist, also ist monoton steigend. Dann zeigst du, dass dies auch für k + 1 gilt.
– Induktionsannahme: ist monoton steigend bis .
– Du möchtes zeigen: $a_{k+1} = 2^{k+1}$ ist größer als .
– Berechnung: $a_{k+1} = 2^{k+1} = 2 \cdot 2^k$ .
– Da positiv ist und wir es mit 2 multiplizieren, ist $2 \cdot 2^k$ größer als .
– Also $a_{k+1} > a_k$ , was zeigt, dass die Folge monoton wachsend ist.

Folgen Mathe — Beschränktheit

im Videozur Stelle im Video springen

Eine Folge (a_n) ist beschränkt, wenn es zwei reelle Zahlen a und b gibt, sodass a ≤ (a_n) ≤ b für alle $n \in \mathbb{N}$ . Das bedeutet, dass sich die Folge zwischen zwei festen Grenzen bewegt.

folgen, folgen mathe, folgen mathematik, folge, mathe folgen, was ist eine folge mathe, mathematik folgen, mathematische folgen, mathematische folge, folgen und reihen, folgen berechnen, folge berechnen, folgen und reihen mathe — Beschränktheit einer Folge

Du unterscheidest dabei 3 Arten von Beschränktheit:

Eine Folge ist nach oben beschränkt, wenn es eine Zahl gibt, die von keinem Glied der Folge überschritten wird. Die Folge $a_n = \frac{1}{n}$ mit den Gliedern $a_1 = 1, a_2 = 0,5, a_3 = 0,33, \ldots$ ist nach oben beschränkt durch die Zahl 1, denn kein Glied der Folge ist größer als 1.
Eine Folge ist nach unten beschränkt, wenn es eine Zahl gibt, die von keinem Folgenglied unterschritten wird. Nehmen wir mit den Gliedern $a_1 = 1, a_2 = 2, a_3 = 3, \ldots$ . Diese Folge ist nach unten durch 1 beschränkt.
Eine Folge ist beidseitig beschränkt, wenn kein Folgenglied die festen Grenzen sowohl nach oben als auch nach unten überschreitet.

Beschränktheit bestimmen

Die Beschränktheit einer Folge kannst du auf verschiedene Weise ermitteln:

Grenzwert:
Eine andere Möglichkeit, ist die Verwendung von Grenzwertbetrachtungen. Wenn die Folge einen Grenzwert hat, dann ist sie beschränkt. Das liegt daran, dass der Grenzwert einer Folge immer in einem endlichen Intervall enthalten ist. Die Folge (a_n) = n^2 divergiert zum Beispiel gegen Unendlich $\infty$ . Der Grenzwert $\infty$ ist nicht in einem endlichen Intervall enthalten. Daher ist die Folge nicht beschränkt.

Induktion:
Die mathematische Induktion kann auch verwendet werden, um die Beschränktheit einer Folge zu beweisen. Nehmen wir als Beispiel die Folge $a_n = \frac{1}{n}$ . Nun willst du beweisen, dass sie nach oben durch 1 beschränkt ist:

Induktionsanfang: Wir starten mit n=1 für die Folge $a_n = \frac{1}{n}$ . Hier ist $a_1 = \frac{1}{1} = 1$ , was unter der Grenze 1 liegt.
Induktionsschritt: Angenommen, für ein k gilt $a_k \leq 1$ . Dann ist $a_{k+1} = \frac{1}{k+1}$ . Da k+1 größer als k ist, ist $\frac{1}{k+1}$ kleiner als $\frac{1}{k}$ , also auch kleiner oder gleich 1. Somit ist die Folge nach oben beschränkt.

Satz von Bolzano-Weierstraß

Von der Beschränktheit und Monotonie kannst du auch auf den Grenzwert einer Folge schließen. Denn der Satz von Bolzano-Weierstraß sagt, dass jede beschränkte monoton wachsende oder monoton fallende Folge einen Grenzwert hat. Beispielsweise die Folge $(a_n) = \frac{1}{n}$ . Da sie monoton fallend und beschränkt durch 0 und 1 ist, hat sie einen Grenzwert — in dem Fall 0.

Arten von Folgen

In der Mathematik gibt es verschiedene Arten von Folgen. Zwei der bekanntesten sind arithmetische und geometrische Folgen. Sie unterscheiden sich in der Art und Weise, wie sich die Folgenglieder zueinander verhalten.

folgen, folgen mathe, folgen mathematik, folge, mathe folgen, was ist eine folge mathe, mathematik folgen, mathematische folgen, mathematische folge, folgen und reihen, folgen berechnen, folge berechnen, folgen und reihen mathe — Arithmetische und geometrische Folge

Arithmetische Folgen: Bei einer arithmetischen Folge ist die Differenz zwischen aufeinanderfolgenden Gliedern konstant. Zum Beispiel, in der Folge $(a_n) = 3, 5, 7, 9, \ldots$ , ist die konstante Differenz 2. Die allgemeine Formel lautet , wobei d die konstante Differenz ist.
Geometrische Folgen: Hier ist das Verhältnis zwischen aufeinanderfolgenden Gliedern konstant. Ein Beispiel ist $(a_n) = 3, 6, 12, 24, \ldots$ , mit einem konstanten Verhältnis von 2. Die allgemeine Formel ist $a_n = a_1 \cdot r^{n-1}$ , wobei r das konstante Verhältnis ist.

Folgen & Reihen

Folgen werden häufig mit Reihen verwechselt. Folgen sind Listen von Zahlen, die nach einer bestimmten Regel gebildet werden. Zum Beispiel ist $a_n = 2, 4, 6, 8 \ldots$ eine Folge, bei der jedes Glied um 2 größer ist als das vorherige.

Reihen hingegen sind die Summen der Glieder einer Folge. Reihen werden in der Form $\sum_{n=1}^{\infty} a_n$ angegeben, was bedeutet, dass du die Glieder a_n von n = 1 bis unendlich summierst. Für unsere Beispielreihe wäre das $\sum_{n=1}^{\infty} 2n$ .

Quiz zum Thema Folgen Mathe

Fibonacci-Folge

Super, jetzt weißt du alles über Folgen! Eine besondere Folge ist die Fibonacci-Folge. Was sie auszeichnet und wie sie entdeckt wurde, erfährst du hier!

Zum Video: Fibonacci Folge

zur Videoseite: Folgen Mathe

Beliebte Inhalte aus dem Bereich Algebra

Fibonacci-Folge

Grenzwertsätze

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .