Wurzel ziehen
Hier erfährst du, wie das Wurzel ziehen in Mathe funktioniert. Wir erklären dir Schritt für Schritt, wie du eine Wurzel einfach berechnen kannst. In unserem Video erklären wir dir anhand von vielen Beispielen, wie du beim Wurzel ziehen vorgehst.
Inhaltsübersicht
Was bedeutet Wurzelziehen?
Eine Wurzel besteht aus folgenden Bausteinen.
Beim Wurzelziehen mit dem Wurzelexponenten 2 machst du im Prinzip einfach das Quadrieren rückgängig. Wenn du die Zahl 2 quadrierst, erhältst du 4.
2² = 2 ⋅ 2 = 4
Ziehst du die Wurzel aus 4, dann erhältst du wieder die 2.

Hinweis: Bei der Quadratwurzel
wird meistens der Wurzelexponent 2 nicht mit aufgeschrieben (![Rendered by QuickLaTeX.com \sqrt[\textcolor{blue}{2}]{\textcolor{red}{4}}=\sqrt{\textcolor{red}{4}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6461d78117332640e19b267051617994_l3.png) ). Das Wurzelziehen nennt man auch Radizieren.
). Das Wurzelziehen nennt man auch Radizieren.
Wurzelberechnung Quadratwurzel
Wurzel ziehen geht oft ganz einfach im Kopf. Schauen wir uns die Wurzelberechnung einmal an einem Beispiel an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel 1
Du sollst die Wurzel aus 16 ziehen.

Dazu überlegst du dir, welche Zahl du mit sich selbst malnehmen kannst, sodass 16 herauskommt. Wenn dir die Zahl nicht direkt einfällt, kannst du auch einfach ein paar Zahlen ausprobieren.
2² = 2 ⋅ 2 = 4 ≠ 16
3² = 3 ⋅ 3 = 9 ≠ 16
4² = 4 ⋅ 4 = 16
Da 4 im Quadrat 16 ergibt, ist die Wurzel aus 16 die Zahl 4.

![Rendered by QuickLaTeX.com \sqrt{16} = \sqrt[\textcolor{blue}{2}]{16} = \sqrt[\textcolor{blue}{2}]{4\cdot 4} = \textcolor{teal}{4}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-93e7a1f3c0046de2671de71a192fa374_l3.png)
Weitere Beispiele
Vorgehensweise Wurzelberechnung
Wir zeigen dir die Wurzelberechnung nun Schritt für Schritt, sodass du auch bei großen Zahlen die Wurzel ziehen kannst.
- Primfaktorzerlegung berechnen
- Fasse gleiche Faktoren in Potenzen zusammen
- Schreibe jeden Faktor unter eine eigene Wurzel
- Schreibe die Wurzel in eine Potenz um
- Ergebnis der Wurzel berechnen
Beispiel 2
Du sollst die Wurzel aus 196 ziehen.

1.Zerlege den Radikanden 196 in Primfaktoren

2. Fasse gleiche Faktoren in Potenzen zusammen
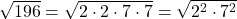
3. Schreibe jeden Faktor unter eine eigene Wurzel

4. Schreibe die Wurzeln als Potenz
![Rendered by QuickLaTeX.com \sqrt[\textcolor{blue}{2}]{2^{\textcolor{teal}{2}}} = 2^{\frac{\textcolor{teal}{2}}{\textcolor{blue}{2}}} = 2^{1} = 2](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-407ff032da3a3b967b4df6984f6478e2_l3.png)
![Rendered by QuickLaTeX.com \sqrt[\textcolor{blue}{2}]{7^{\textcolor{teal}{2}}}= 7^{\frac{\textcolor{teal}{2}}{\textcolor{blue}{2}}} = 7^{1} = 7](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3f6d41217a87b556b27c25afe937b39b_l3.png)
→ ![Rendered by QuickLaTeX.com \sqrt[2]{2^{2}} \cdot \sqrt[2]{7^{2}} = 2 \cdot 7](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-df1953e478b35575d1c63ffff2b0c936_l3.png)
5. Ergebnis der Wurzel berechnen

Weitere Beispiele
![Rendered by QuickLaTeX.com \sqrt{256} = \sqrt[\textcolor{blue}{2}]{2^{\textcolor{teal}{8}}} = 2^{\frac{\textcolor{teal}{8}}{\textcolor{blue}{2}}} = 2^{\frac{4}{1}} = 2^{4} = 16](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-64f99fadbbf1ac3e58e1b5ce44827133_l3.png)
![Rendered by QuickLaTeX.com \sqrt{144} = \sqrt[\textcolor{blue}{2}]{2^{\textcolor{teal}{4}} \cdot 3^{\textcolor{teal}{2}}} = \sqrt[\textcolor{blue}{2}]{2^{\textcolor{teal}{4}}} \cdot \sqrt[\textcolor{blue}{2}]{3^{\textcolor{teal}{2}}} = 2^{\frac{\textcolor{teal}{4}}{\textcolor{blue}{2}}} \cdot 3^{\frac{\textcolor{teal}{2}}{\textcolor{blue}{2}}} = 2^{2} \cdot 3 = 4 \cdot 3 = 12](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c4036de2189089fc67f94c44dd654e11_l3.png)
Achtung: Bei der Wurzelberechnung kannst du aus negativen Zahlen keine Wurzel ziehen.
Beispiel 1
Du sollst die dritte Wurzel aus 8 ziehen.
![Rendered by QuickLaTeX.com \sqrt[3]{8}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-45490844932db074ed67fc415525e22a_l3.png)
1.Zerlege die Zahl unter der Wurzel in Primfaktoren
![Rendered by QuickLaTeX.com \sqrt[3]{8}=\sqrt[3]{2 \cdot 4}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0a0223454e0090feb0172b37f7faaeab_l3.png)
![Rendered by QuickLaTeX.com =\sqrt[3]{2 \cdot 2 \cdot 2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b81f0b9dbec1eb329a57d7349cec40ea_l3.png)
2. Fasse gleiche Faktoren zu Potenzen zusammen
![Rendered by QuickLaTeX.com \sqrt[3]{8} = \sqrt[3]{2^{3}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ab5fc2915e9895040a68ffc6ac9bcbb3_l3.png)
3. Schreibe jeden Faktor unter eine eigene Wurzel: Da du hier nur den Faktor 2 hast, kann der Schritt ausgelassen werden.
4. Schreibe die Wurzel in eine Potenz um
![Rendered by QuickLaTeX.com \sqrt[\textcolor{blue}{3}]{2^{\textcolor{teal}{3}}} = 2^{\frac{\textcolor{teal}{3}}{\textcolor{blue}{3}}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4a643adc4d3fce753a393bc335536fff_l3.png)
5. Ergebnis der Wurzel berechnen
![Rendered by QuickLaTeX.com \sqrt[3]{8}=2^{\frac{\textcolor{teal}{3}}{\textcolor{blue}{3}}} = 2^{1} = 2](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f717a463f15a5e9e7ed4e09decbe2610_l3.png)
Beispiel 2
Du sollst die vierte Wurzel aus 625 berechnen.
![Rendered by QuickLaTeX.com \sqrt[4]{\textcolor{red}{625}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-54385d0982c626ae9bc7369f32ee7322_l3.png)
1.Zerlege den Radikanden 625 in Primfaktoren
![Rendered by QuickLaTeX.com \begin{align*} \sqrt[4]{625} &= \sqrt[4]{ 5\cdot 125} \\ &= \sqrt[4]{5 \cdot 5 \cdot 25} \\ &= \sqrt[4]{5 \cdot 5 \cdot 5 \cdot 5} \end{align*}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-812fbf4c15404407041c42bde2af732f_l3.png)
2. Fasse gleiche Faktoren in Potenzen zusammen
![Rendered by QuickLaTeX.com \sqrt[4]{625} = \sqrt[4]{5\cdot 5 \cdot 5 \cdot 5} = \sqrt[4]{5^4}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-69d809460081fef70603864b3ca19e7f_l3.png)
3. Schreibe jeden Faktor unter eine eigene Wurzel: Da du hier nur den Faktor 5 hast, kann der Schritt ausgelassen werden.
4. Wurzel in Potenz umschreiben
![Rendered by QuickLaTeX.com \sqrt[\textcolor{blue}{4}]{5^\textcolor{teal}{4}} = 5^{\frac{\textcolor{teal}{4}}{\textcolor{blue}{4}}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8e9c61123645859686ddd1a20db943b6_l3.png)
5. Ergebnis der Wurzel berechnen

Beispiel
Du sollst folgende Wurzel berechnen.
![Rendered by QuickLaTeX.com \sqrt[3]{27(x-1)^{3}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-56b04b1ae12bdd8d4ef84abf33bb9a5b_l3.png)
1.Zerlege den Radikanden in Primfaktoren:
![Rendered by QuickLaTeX.com \sqrt[3]{3 \cdot 3 \cdot 3 \cdot (x-1)^{3}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a6e8c62909cf06e150f385e8c5cf1f58_l3.png)
2. Fasse gleiche Faktoren zu Potenzen zusammen
![Rendered by QuickLaTeX.com \sqrt[3]{3^{3} \cdot (x-1)^{3}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b27f82070c5c5f7fcc815fca280030ce_l3.png)
3. Schreibe jeden Faktor unter eine eigene Wurzel
![Rendered by QuickLaTeX.com \sqrt[3]{3^{3}} \cdot \sqrt[3]{(x-1)^{3}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-180fe163fac2809b854d040433995767_l3.png)
4. Wurzel in Potenz umschreiben
![Rendered by QuickLaTeX.com \sqrt[3]{3^{3}} \cdot \sqrt[3]{(x-1)^{3}} = 3^{\frac{3}{3}} \cdot (x-1)^{\frac{3}{3}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3e6a50b1a1e1fba87dbd07590f18da05_l3.png)
5. Ergebnis der Wurzel berechnen

Wurzel ziehen — häufigste Fragen
(ausklappen)
Wurzel ziehen — häufigste Fragen
(ausklappen)-
Was bedeutet Wurzel ziehen mathematisch, und warum ist das das Gegenteil von Quadrieren?Wurzel ziehen heißt: Du suchst die Zahl, deren Quadrat wieder den Radikanden (Zahl unter der Wurzel) ergibt. Konkret gilt:
 , weil
, weil  . Deshalb ist Wurzelziehen das Gegenteil von Quadrieren, weil du damit das Potenzieren mit
. Deshalb ist Wurzelziehen das Gegenteil von Quadrieren, weil du damit das Potenzieren mit  rückgängig machst.
rückgängig machst.
-
Wie berechne ich die Quadratwurzel aus einer großen Zahl mit Primfaktorzerlegung?Eine Quadratwurzel über Primfaktorzerlegung berechnest du, indem du den Radikanden in Primfaktoren zerlegst und gleiche Faktoren als Potenzen schreibst. Danach halbierst du die Exponenten. Zum Beispiel:
 , also
, also  .
.
-
Warum kann ich aus einer negativen Zahl keine Quadratwurzel ziehen?Aus einer negativen Zahl kannst du in den reellen Zahlen keine Quadratwurzel ziehen, weil beim Quadrieren nie etwas Negatives entsteht. Jede reelle Zahl erfüllt
 . Deshalb hat die Gleichung
. Deshalb hat die Gleichung  keine reelle Lösung, also gibt es keine reelle Zahl mit
keine reelle Lösung, also gibt es keine reelle Zahl mit  .
.
-
Wie berechne ich eine Wurzel mit Wurzelexponent 3 Schritt für Schritt?Eine dritte Wurzel berechnest du, indem du den Radikanden in Primfaktoren zerlegst und Dreiergruppen bildest. Zum Beispiel:
![Rendered by QuickLaTeX.com \sqrt[3]{8} = \sqrt[3]{2 \cdot 2 \cdot 2} = \sqrt[3]{2^3}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-b472662f5cd7ffffa31c9e963105b39e_l3.png) . Danach schreibst du als Potenz:
. Danach schreibst du als Potenz: ![Rendered by QuickLaTeX.com \sqrt[3]{2^3} = 2^{\frac{3}{3}} = 2](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-dd17659497e259d3e225316d2b669bcf_l3.png) .
.
-
Wie ziehe ich eine Wurzel mit Wurzelexponent 3, wenn im Radikanden auch Variablen stehen, zum Beispiel 27 mal (x minus 1) hoch 3?Bei
![Rendered by QuickLaTeX.com \sqrt[3]{27(x-1)^3}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-4b8aada0a5d49ded654a057803e248f2_l3.png) zerlegst du zuerst
zerlegst du zuerst  und nutzt Potenzen. Konkret:
und nutzt Potenzen. Konkret:  , also
, also ![Rendered by QuickLaTeX.com \sqrt[3]{27(x-1)^3} = \sqrt[3]{3^3 \cdot (x-1)^3}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-cd214d61ffb67395e9d1383da8b98785_l3.png) . Dann trennst du:
. Dann trennst du: ![Rendered by QuickLaTeX.com \sqrt[3]{3^3}\cdot\sqrt[3]{(x-1)^3} = 3 \cdot (x-1) = 3x - 3](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-447ca793f6de65712ddf839ce25a72ef_l3.png) .
.
Wurzelberechnung und Wurzelgesetze
Um deine Prüfung zu bestehen, musst du dir unbedingt noch unser Video zu den Wurzelgesetzen anschauen. Dort erfährst du, wie das Wurzel rechnen mit den Grundrechenarten funktioniert. Schau es dir direkt an!




