Schwingungsdauer und Amplitude
Für jedes Pendel lässt sich die Schwingungsdauer und Amplitude berechnen oder bestimmen. In diesem Beitrag zeigen wir dir alles, was du darüber wissen musst und erklären dir die Formeln anschaulich.
Noch besser verstehst du das Thema, wenn du dir unser Video dazu anschaust! Dort ist das Thema in kürzester Zeit aufbereitet.
Inhaltsübersicht
Schwingungsdauer
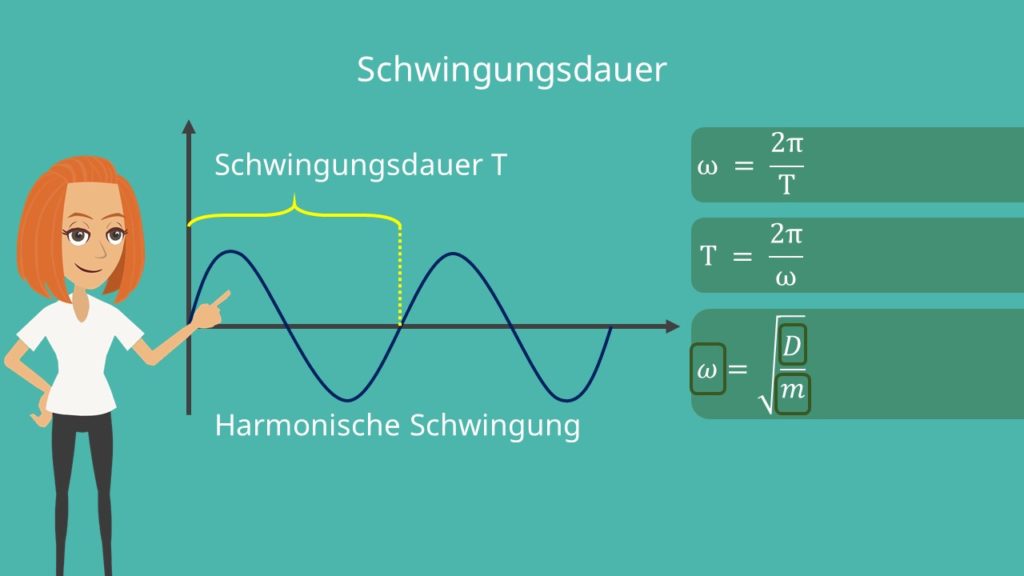
Die Zeit für einen Schwingungsvorgang wird Schwingungsdauer genannt. Es ist somit die Zeit, die ein schwingender Körper für eine Hin- und Her-Bewegung benötigt. Meistens wird sie mit dem Formelzeichen T symbolisiert und hat die Einheit Sekunde.
Am Beispiel der harmonischen Schwingung und der damit einhergehenden Sinuskurve, soll der Begriff der Schwingungsdauer erklärt werden. Später soll die Schwingungsdauer dann auf komplexere Schwingungen übertragen werden.
Schwingungsdauer berechnen
Die Schwingungsdauer kann mit der Hilfe der Winkelgeschwindigkeit für Kreisbewegungen bestimmt werden. Hier ergibt sich folgender Zusammenhang:
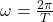
Daraus kann zur Schwingungsdauer eines harmonischen Oszillators folgende Formel festgehalten werden:
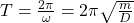
Die Masse ist dabei m und D wird Richtgröße genannt. Bei einer harmonischen Schwingung ist dies der Fall, da sich aus der Bewegungsgleichung für jene Art des Pendels eine Eigenkreisfrequenz von
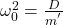
ergibt. Bei einer Schwingung an einem Federpendel ist D die materialabhängige Federkonstante . Für ein Fadenpendel zeigen wir dir im Kapitel Schwingungsdauer Fadenpendel wie du die Richtgröße richtig definierst.
An der Formel kann festgestellt werden, dass je größer die Masse ist, desto größer ist die Schwingungsdauer. Genauso gilt, je größer die Richtgröße, desto kleiner wird die Schwingungsdauer.
Für eine gedämpfte Schwingung ergibt sich eine andere Eigenfrequenz . Allgemein ist die gegeben durch:
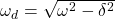
Von der normalen Eigenfrequenz wird die Abklingkonstante für die Schwingung abgezogen, um die gedämpfte Eigenfrequenz zu erhalten. Deshalb kann im Folgenden nur die harmonische Pendelbewegung betrachtet werden. Für die gedämpfte muss dann nur in jedem Fall die jeweilige Abklingkonstante abgezogen werden. Möchtest du genaueres zu den gedämpften Pendeln wissen? Dann haben wir dir hier unseren Artikel dazu verlinkt.
Schwingungsdauer Federpendel
In unserem Artikel zum Thema ungedämpftes Federpendel , wird die Pendelbewegung mit der Hilfe von folgender Differentialgleichung beschrieben:
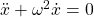
 ist die ungedämpfte Eigenkreisfrequenz und x die Auslenkung, mit ihrer jeweiligen zeitlichen Ableitung. Über das Gleichsetzen der allgemeinen Definition der Eigenfrequenz mit der, aus der Differentialgleichung bestimmten Frequenz, kann die Schwingungsdauer T bestimmt werden.
ist die ungedämpfte Eigenkreisfrequenz und x die Auslenkung, mit ihrer jeweiligen zeitlichen Ableitung. Über das Gleichsetzen der allgemeinen Definition der Eigenfrequenz mit der, aus der Differentialgleichung bestimmten Frequenz, kann die Schwingungsdauer T bestimmt werden.
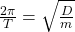
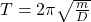
Die Masse wird durch ein m symbolisiert und D ist die materialabhängige Federkonstante. Diese Formel drückt nun die benötigte Zeit für eine Schwingung des Pendels aus.
Schwingungsdauer Fadenpendel
In dem Artikel über harmonische Schwingungen wird die Differentialgleichung des Fadenpendels ohne Reibungsverluste hergeleitet. Falls du dich mehr mit der Herleitung beschäftigen möchtest, findest du den Beitrag hier. Die Schwingungsgleichung lautet dann:
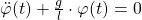
Der Winkel der Auslenkung ist dabei und die Länge des Pendels ist l. Der Ortsfaktor wird durch g dargestellt.
Die allgemeine Gleichung für die Schwingungsdauer eines harmonischen Oszillators wurde bereits aufgestellt. Da es sich hier beim Fadenpendel auch um eine harmonische Schwingung handelt, muss die Richtgröße D des Pendels richtig bestimmt werden. Die Rückstellkraft eines Fadenpendels ist gegeben durch:
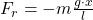
Die Masse des Pendelkörpers ist wieder m. Nun wird diese Kraft mit der, der für das Rückschwingen des harmonischen Federpendels verantwortlichen Kraft gleichgesetzt und nach der Federkonstante, beziehungsweise Richtgröße D aufgelöst. In unserem Artikel zum Federpendel haben wir dir die Grundlagen zu diesem Pendel aufbereitet. Der Weg bis zur Ruhelage wird durch x ausgedrückt:
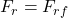
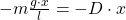
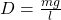
Dies kann jetzt in die Schwingungsdauer für das Federpendel eingesetzt werden.
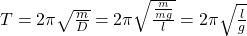
So schwingt ein harmonisches Fadenpendel mit dieser Schwingungsdauer.
Schwingungsdauer physikalisches Pendel
In unserem Artikel zum physikalischen Pendel haben wir die Schwingungsdauer und Frequenz definiert. Dabei muss immer das Trägheitsmoment J bezüglich des Aufhängepunktes mitberücksichtigt werden. Die Definition lautet:
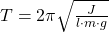
Die Masse ist m, der Ortsfaktor ist gegeben durch g und l symbolisiert den Abstand vom Schwerpunkt des Pendelkörpers zum Aufhängepunkt.
Schwingungsdauer und Frequenz
Die Frequenz wird durch ein f symbolisiert und eine Einheit von 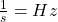 [Hertz]. Sie ist der Kehrwert der Schwingungsdauer T:
[Hertz]. Sie ist der Kehrwert der Schwingungsdauer T:
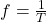
Damit gibt die Frequenz also die Anzahl an Schwingungen an, die ein Pendelkörper in einem bestimmten Zeitintervall vollführt.
Amplitude
Hier wird das gleiche Vorgehen, wie bei der Schwingungsdauer verwendet. Zuerst wird die Amplitude anhand der harmonischen Schwingung erklärt, um sie dann auf andere Schwingungsarten zu übertragen.
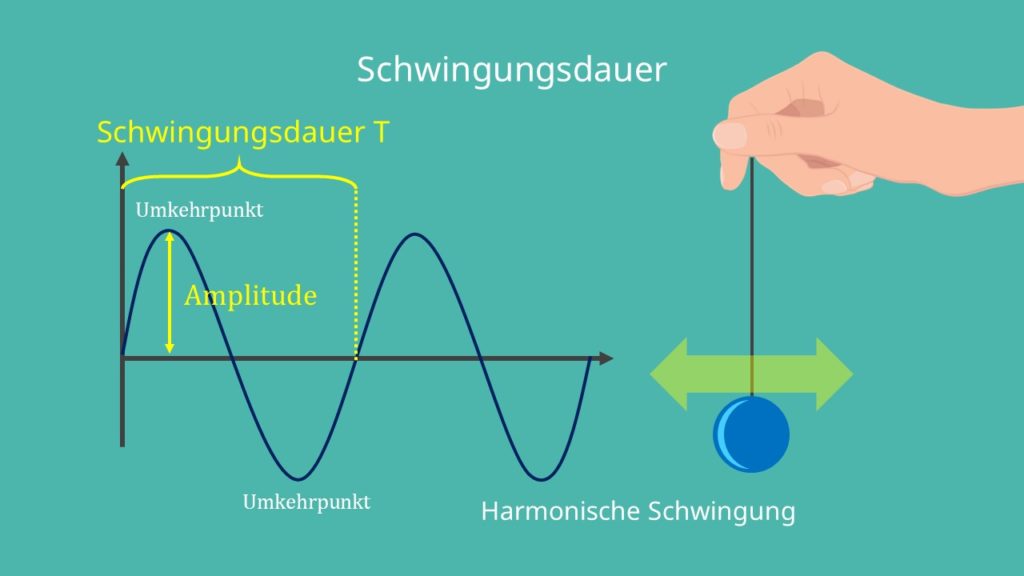
Die Amplitude ist die betragsmäßig größte Auslenkung eines Schwingungsvorgangs. Also der Maximalwert der Auslenkung. Sie wird meistens mit bezeichnet und hat als Einheit eine Längeneinheit. Die Amplitude ist nach ihrer Definition immer positiv. Differenziert werden muss hier zum Begriff der Auslenkung. Jene wird auch als Elongation bezeichnet und ist der Abstand von dem Pendelkörper zu dem Zeitpunkt t von der Ruhelage der Schwingung. Die Auslenkung kann im Gegensatz zur Amplitude positiv oder negativ sein. Die Elongation eines Pendels ist meistens über eine Funktion definiert, genauer über eine Zeit-Ort-Funktion. Durch Einsetzen eines Zeitpunktes t kann der Wert der Auslenkung in einer Längeneinheit bestimmt werden. Das Formelzeichen ist x(t).
Bei der harmonischen Schwingung ist die Amplitude immer gleich groß. In dem obigen Bild sind daher auch die Beträge der Umkehrpunkte immer gleich hoch eingezeichnet.
Amplitude berechnen
Für harmonische Schwingungen ist das Zeit-Orts-Gesetz gegeben durch:
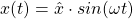
Dieses stellt einen Zusammenhang zwischen der Auslenkung x(t), der Amplitude , der Winkelgeschwindigkeit beziehungsweise Frequenz und der Zeit t her.
Falls du noch mehr Gesetze in diesem Zusammenhang kennenlernen willst, dann schau bei unserem Beitrag zur harmonischen Schwingung vorbei.
Bei der gedämpften Schwingung verändert sich dieses Gesetz ein wenig. Es muss die Dämpfungskonstante mitbetrachtet werden, denn die Auslenkung nimmt mit der Zeit durch die Dämpfung ab. Die Auslenkung der gedämpften Schwingung kann wie folgt physikalisch beschrieben werden:
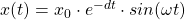 bzw.
bzw. 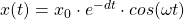
x0 ist die Anfangsauslenkung des Pendels. gibt hierbei die Abnahme der Amplitude in Abhängigkeit von der Zeit an. Die Dämpfungskonstante mit Formelzeichen , manchmal auch , gibt die Stärke der Dämpfung an.
Des Weiteren kann die maximale Auslenkung bestimmt werden. Die maximale Auslenkung zu einem bestimmten Zeitpunkt ergibt sich zu:
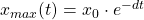
Aufgepasst werden muss, dass es sich bei der maximalen Auslenkung xmax nicht unbedingt um die Amplitude handeln muss.
Amplitude und Frequenz
Die Amplitude ist die betragsmäßig größte Auslenkung einer Schwingung. Die Frequenz gibt an, wie oft ein Pendelkörper in einem bestimmten Zeitintervall schwingt.
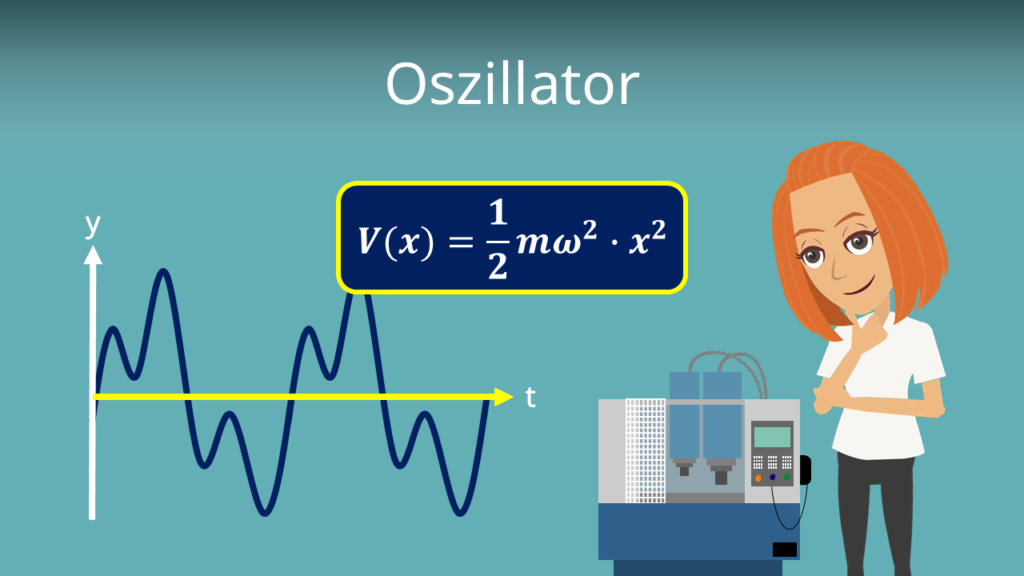
Beide Werte sind wichtige Parameter für den sogenannten Oszillator. Darunter kannst du dir ein schwingungsfähiges System vorstellen, das sich um seine Ruhelage bewegt. Schau dir gerne unseren Beitrag dazu an, wenn du mehr über die Funktionsweise und die Arten von Oszillatoren erfahren möchtest.