Harmonische Schwingung
Eine harmonische Schwingung beschreibt einen harmonischen Oszillator, der sinusförmig um seine Ruhelage schwingt. Es gibt verschiedene harmonische Oszillatoren, wie das Fadenpendel oder das Federpendel . In unserem Video erklären wir dir, durch welche Bedingungen eine harmonische Schwingung charakterisiert ist. Zusätzlich lernst du, wie eine Bewegung auf einen Kreis mit der Sinusfunktion zusammenhängt und wie die Schwingung eines Faden- und Federpendels durch eine Schwingungsgleichung beschrieben werden kann.
Du hast nicht so viel Zeit, alles zu lesen? Kein Problem! Genau dafür haben wir ein Video erstellt. Schau es dir an, damit du innerhalb von kürzester Zeit alles Wichtige zur Harmonischen Schwingung erfährst!
Inhaltsübersicht
Harmonische Schwingung Definition
Eine harmonische Schwingung zeichnet sich durch eine lineare Rückstellgröße aus und kann durch eine sinusförmige Funktion beschrieben werden. Als Schwingungen, auch Oszillationen genannt, bezeichnet man allgemein zeitliche Schwankungen von Zustandsgrößen eines Systems. Ein schwingendes System, welches eine harmonische Schwingung ausführt, wird auch harmonischer Oszillator genannt.
Man unterscheidet verschiedene Arten von Schwingungen. Es gibt zum Beispiel periodische, nicht periodische, lineare, nichtlineare, gedämpfte oder ungedämpfte Schwingungen. Im Folgenden werden wir uns auf die Beschreibung harmonischer Schwingungen beschränken.
Eine harmonische Schwingung kann durch die folgenden zwei Bedingungen charakterisiert werden. Zum einen kann man die Bewegung eines schwingenden Körpers mit der Projektion einer Kreisbewegung beschreiben. Dies entspricht einer Sinus- bzw. Kosinusfunktion, zum Beispiel

Zum anderen ist eine harmonische Schwingung durch das lineare Kraftgesetz darstellbar. Dieses besagt, dass die rücktreibende Kraft auf einen schwingenden Körper proportional zur Auslenkung aus der Ruhelage und dieser entgegengesetzt ist. Dieser Zusammenhang kann durch die Formel

ausgedrückt werden. Diese Gleichung beschreibt die Rückstellkraft eines an einer Feder befestigten Körpers. Die Variable  entspricht hierbei der Federkonstanten. Genaueres findest du in unserem Artikel Schwingungsgleichung Federpendel.
entspricht hierbei der Federkonstanten. Genaueres findest du in unserem Artikel Schwingungsgleichung Federpendel.
Harmonische Schwingung Formel
Eine harmonische Schwingung wird durch die Formel

beschrieben. Hierbei repräsentiert  die Auslenkung bzw. Elongation des schwingenden Körpers,
die Auslenkung bzw. Elongation des schwingenden Körpers,  die Amplitude der Schwingung,
die Amplitude der Schwingung,  die Frequenz beziehungsweise Winkelgeschwindigkeit
,
die Frequenz beziehungsweise Winkelgeschwindigkeit
,  die Zeit und
die Zeit und  die Phasenkonstante. Diese Funktion gibt einen Zusammenhang zwischen Ort und Zeit eines schwingenden Körpers und wird deshalb Zeit-Orts-Gesetz
genannt.
die Phasenkonstante. Diese Funktion gibt einen Zusammenhang zwischen Ort und Zeit eines schwingenden Körpers und wird deshalb Zeit-Orts-Gesetz
genannt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
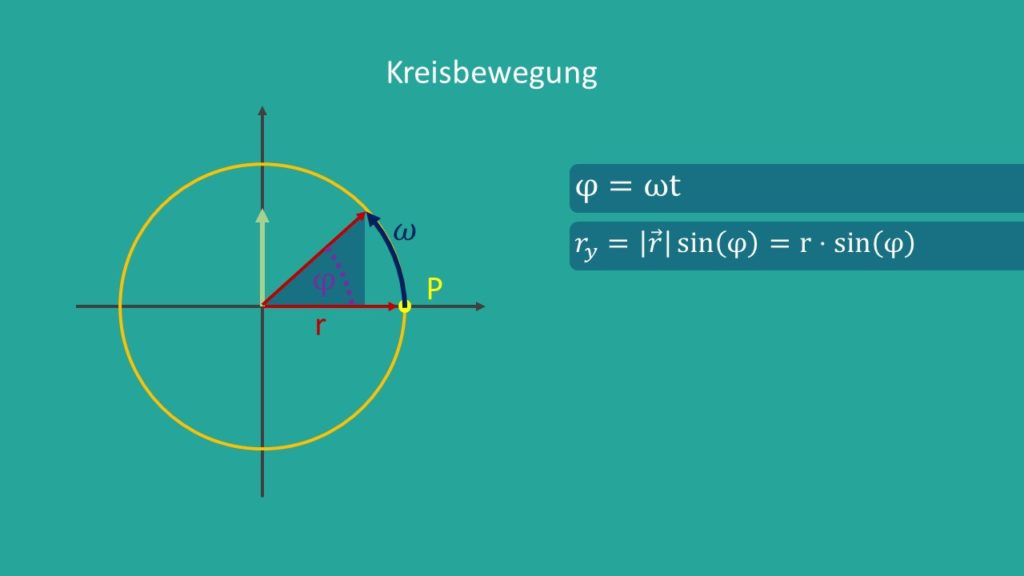
Harmonische Schwingung Kreisbewegung
Wie oben erwähnt, kann eine harmonische Schwingung durch die Projektion einer Kreisbewegung dargestellt werden. Um die Bewegung zu veranschaulichen, geht man von einem Punkt  auf einem Kreis mit dem Radius
auf einem Kreis mit dem Radius  aus. Dieser Punkt bewege sich mit konstanter Winkelgeschwindigkeit
aus. Dieser Punkt bewege sich mit konstanter Winkelgeschwindigkeit  um den Ursprung eines Koordinatensystems. Zum Zeitpunkt
um den Ursprung eines Koordinatensystems. Zum Zeitpunkt  habe der Punkt die Position
habe der Punkt die Position 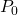 . An diesem Punkt ist die y-Komponente des Punktes null, da dieser auf der x-Achse liegt.
. An diesem Punkt ist die y-Komponente des Punktes null, da dieser auf der x-Achse liegt.
Bewegt sich nun der Punkt gegen den Uhrzeigersinn, dann nimmt die y-Komponente des Punktes zuerst zu, bis der Vektor 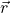 einen Winkel von 90° zurückgelegt hat.
einen Winkel von 90° zurückgelegt hat.
In der oberen Abbildung kann man erkennen, dass die y-Komponente durch  berechnet werden kann. Da sich der Vektor
berechnet werden kann. Da sich der Vektor 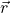 mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit  bewegt, ist der zurückgelegte Winkel nach der Zeit
bewegt, ist der zurückgelegte Winkel nach der Zeit  durch
durch  gegeben. Die Komponente
gegeben. Die Komponente  lässt sich dann leicht über
lässt sich dann leicht über


bestimmen.
Nachdem die y-Komponente ihr Maximum erreicht hat, nimmt diese dann ab, bis der Vektor 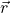 einen Winkel von 180◦ zurückgelegt hat. An diesem Punkt ist die y-Komponente des Punktes null. Die weitere Bewegung des Punktes ist dadurch charakterisiert, dass die y-Komponente bei 270° ihr Minimum erreicht und danach wieder zu nimmt, bis der Punkt zu seinem Ausgangspunkt zurückkehrt. Die Projektion der Bewegung des Punktes auf die y-Achse führt also dazu, dass der Vektor
einen Winkel von 180◦ zurückgelegt hat. An diesem Punkt ist die y-Komponente des Punktes null. Die weitere Bewegung des Punktes ist dadurch charakterisiert, dass die y-Komponente bei 270° ihr Minimum erreicht und danach wieder zu nimmt, bis der Punkt zu seinem Ausgangspunkt zurückkehrt. Die Projektion der Bewegung des Punktes auf die y-Achse führt also dazu, dass der Vektor  ein periodisches Verhalten zeigt. Dieser oszilliert zwischen den Werten
ein periodisches Verhalten zeigt. Dieser oszilliert zwischen den Werten  und
und  . Zeichnet man den Vektor
. Zeichnet man den Vektor  in Abhängigkeit der Zeit, so erhält man eine Sinuskurve. Die harmonische Schwingung kann also mit einer Sinusfunktion dargestellt werden. Eine genauere Erklärung findest du in unserem Beitrag zur Schwingungsdauer und Amplitude
.
in Abhängigkeit der Zeit, so erhält man eine Sinuskurve. Die harmonische Schwingung kann also mit einer Sinusfunktion dargestellt werden. Eine genauere Erklärung findest du in unserem Beitrag zur Schwingungsdauer und Amplitude
.
Geschwindigkeit und Beschleunigung einer Schwingung
Aus dem oben beschriebenen Zeit-Orts-Gesetz, welches eine harmonische Schwingung beschreibt, lässt sich durch Ableiten dieser Funktion das Zeit-Geschwindigkeits-Gesetz und das Zeit-Beschleunigungs-Gesetz bestimmen. Das Zeit-Orts-Gesetz ist gegeben durch

wobei  die Amplitude repräsentiert. Durch Ableiten dieser Funktion erhält man das Zeit-Geschwindigkeits-Gesetz, das die Geschwindigkeit in Abhängigkeit der Zeit angibt
die Amplitude repräsentiert. Durch Ableiten dieser Funktion erhält man das Zeit-Geschwindigkeits-Gesetz, das die Geschwindigkeit in Abhängigkeit der Zeit angibt

Mit der Substitution  lässt sich dieser Ausdruck auch vereinfachen. Dafür folgt dann
lässt sich dieser Ausdruck auch vereinfachen. Dafür folgt dann

Leitet man diese Funktion erneut ab, so führt dies auf das Zeit-Beschleunigungs-Gesetz

mit  .
.
Fadenpendel
Das Fadenpendel besteht aus einem Faden der Länge  , an dem ein Körper der Masse
, an dem ein Körper der Masse  aufgehängt ist. Wird der Körper aus der Ruhelage um den Winkel
aufgehängt ist. Wird der Körper aus der Ruhelage um den Winkel  ausgelenkt, dann wirkt auf den Körper eine Tangentialkraft
ausgelenkt, dann wirkt auf den Körper eine Tangentialkraft  , die tangential zur Pendelbahn ist. Falls nur diese Kraft auf den Körper von außen einwirkt, verursacht sie eine harmonische Schwingung des Körpers. Über trigonometrische Funktionen lässt sich die Tangentialkraft ausdrücken durch
, die tangential zur Pendelbahn ist. Falls nur diese Kraft auf den Körper von außen einwirkt, verursacht sie eine harmonische Schwingung des Körpers. Über trigonometrische Funktionen lässt sich die Tangentialkraft ausdrücken durch

Hierbei beschreibt  die Gewichtskraft des Körpers. Da die Tangentialkraft immer zur Ruhelage zeigt und somit immer entgegen der Auslenkung, ist die Tangentialkraft negativ
die Gewichtskraft des Körpers. Da die Tangentialkraft immer zur Ruhelage zeigt und somit immer entgegen der Auslenkung, ist die Tangentialkraft negativ

Aufgrund des Aktionsprinzips von Newton (2. Newtonsche Axiom ) kann die Tangentialkraft auch durch

dargestellt werden.  repräsentiert dabei die Tangentialbeschleunigung. Diese Tangentialbeschleunigung lässt sich auch über die Winkelbeschleunigung
repräsentiert dabei die Tangentialbeschleunigung. Diese Tangentialbeschleunigung lässt sich auch über die Winkelbeschleunigung  ausdrücken
ausdrücken

In unserem Fall stellt die Tangentialkraft die einzige äußere Kraft dar, so dass man folgende nichtlineare Differentialgleichung erhält


Für kleine Winkel kann der Sinus wie folgt genähert werden
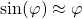
Dies führt dann auf folgende Schwingungsgleichung

Die Lösung  dieser Differentialgleichung ist eine Funktion, die sich nach zweimaligem Differenzieren bis auf das Vorzeichen reproduziert. Dieses Verhalten erfüllen die Sinus- und Kosinusfunktion, sodass die allgemeine Lösung durch eine Linearkombination dieser Funktionen dargestellt werden kann
dieser Differentialgleichung ist eine Funktion, die sich nach zweimaligem Differenzieren bis auf das Vorzeichen reproduziert. Dieses Verhalten erfüllen die Sinus- und Kosinusfunktion, sodass die allgemeine Lösung durch eine Linearkombination dieser Funktionen dargestellt werden kann

Diese allgemeine Lösung beschreibt eine Überlagerung zweier Schwingungen und ist deshalb äquivalent zu einer Schwingung mit derselben Frequenz und einer Phasenverschiebung 

Der Faktor  ist eindeutig durch Anfangsbedingungen festgelegt.
ist eindeutig durch Anfangsbedingungen festgelegt.
Harmonische Schwingung: Federpendel
Das Federpendel besteht aus einer Feder, an dem ein Körper angebracht ist. Wird der Körper aus der Ruhelage ausgelenkt, dann beginnt er auf und ab zu schwingen. Die Bewegung des Federpendels kann im ungedämpften Fall durch die homogene Differentialgleichung

beschrieben werden und entspricht einer harmonischen Schwingung. Hierbei repräsentiert  die Masse des Körpers und
die Masse des Körpers und  die Federkonstante. Für eine ausführliche Behandlung des Federpendels, verweisen wir auf unseren Artikel Federpendel
.
die Federkonstante. Für eine ausführliche Behandlung des Federpendels, verweisen wir auf unseren Artikel Federpendel
.