Betrag
Du willst wissen, was der Betrag ist und wie du damit rechnen kannst? Dann bist du hier und in unserem Video genau richtig!
Inhaltsübersicht
Was ist ein Betrag?
Der Betrag einer Zahl ist der Abstand dieser Zahl vom Nullpunkt der Zahlengeraden. Du schreibst ihn mithilfe von Betragsstrichen:
Beispiel: |3| = 3 und |-3| = 3
Um den Betrag (oder auch Absolutbetrag) zu bilden, musst du das Vorzeichen der Zahl weglassen:
- 3 hat kein Vorzeichen (positive Zahl ). Deshalb ist der Betrag einfach 3.
- –3 hat ein Minus als Vorzeichen (negative Zahl ). Der Betrag davon ist 3 (ohne Vorzeichen). Er ist also das Negative der ursprünglichen Zahl.
Betrag berechnen Beispiele
Schau dir gleich ein paar Beispiele zu Beträgen an.
Beispiel 1: Betrag einer Zahl
a) |-5| = 5, weil bei Beträgen das Minus weggelassen wird. Das bedeutet, dass der Abstand von -5 zum Nullpunkt genau 5 ist.
b) |41| = 41, weil 41 schon eine positive Zahl ist. Du kannst also kein Vorzeichen weglassen.
c) 
, weil bei Beträgen das Minus weggelassen wird.
Beispiel 2: Rechnen mit Beträgen (Terme)
Manchmal musst du nicht nur einzelne Zahlen im Betrag berechnen, sondern Rechnungen. Die nennst du dann Terme .
a) |4 • (-2)| + 1 = ?
- Schritt 1: Löse alle Rechnungen innerhalb der Beträge.
|4 • (-2)| + 1 = |-8| + 1
- Schritt 2: Berechne die Beträge selbst.
|4 • (-2)| + 1 = |-8| + 1 = 8 + 1
- Schritt 3: Betrag ausrechnen.
|4 • (-2)| + 1 = |-8| + 1 = 8 + 1 = 9
b) |5 – 9| + |(-1) • (-3)| = |-4| + |3| = 4 + 3 = 7
c) 3 • ||1 – 4| • (-2)| = 3 • ||-3| • (-2)| = 3 • |3 • (-2)| = 3 • |-6| = 3 • 6 = 18
Betrag Rechenregeln
Damit du noch einfacher den Betrag berechnen kannst, solltest du einige Betrag Regeln kennen. Hier siehst du sie jeweils mit Beispiel. Die Buchstaben a und b stehen dabei für eine beliebige Zahl:
| Betragsregeln | Beispiel |
| Der Betrag von 0 ist immer 0. | |0| = 0 |
| Beträge sind immer nicht negativ, also größer gleich 0 (≥ 0). | |-3| = 3 ≥ 0, |2| = 2 ≥ 0 |
| Malrechnung: |a • b| = |a| • |b| | |3 • (-2)| = |3| • |-2| |
| Potenz: |ab| = |a|b | |25| = |2|5 |
Bruch: 
|
 |
| Dreiecksungleichung : |a + b| ≤ |a| + |b| | |-5 + 3| ≤ |-5| + |3| |
Expertenwissen: Betragsfunktion und Anwendungen
Du kannst Beträge auch als Funktion betrachten. Dafür brauchst du zuerst die formale Betrag Definition:
![\[|x| = \left\{\begin{array}{11} x, & x>0 \\ -x, & x<0 \end{array}\right\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-41986599de75216de2f7eeb220de4068_l3.png "Rendered by QuickLaTeX.com")
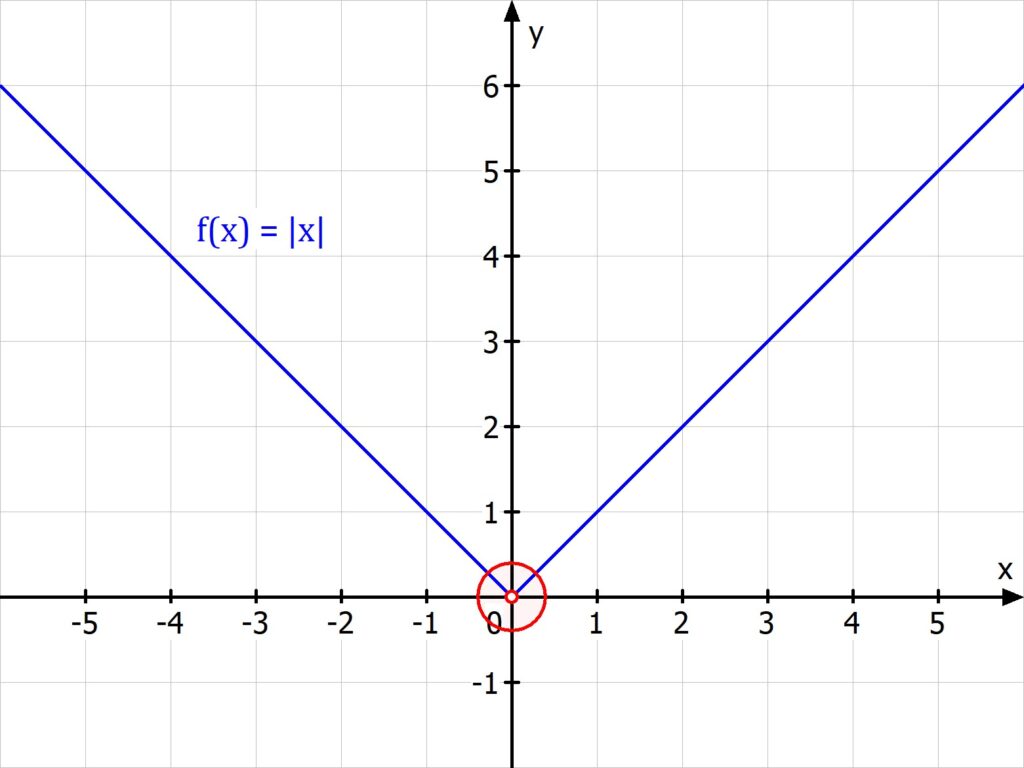
Die Betragsfunktion f(x) = |x| sieht dann so aus:
Wenn Beträge in einer Funktion vorkommen, betrachtest du die Funktion jeweils zwischen den Knickstellen.
Du kannst dann verschiedene Eigenschaften der Betragsfunktion ermitteln:
-
Ableitung
:
Auch hier gelten die Ableitungsregeln ganz normal.![\[f'(x) = \frac{x}{|x|}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d88961b3c0889727c17c94d70d90040b_l3.png "Rendered by QuickLaTeX.com")
- Stetigkeit und Differenzierbarkeit : f(x) = |x| ist stetig, aber an x = 0 nicht differenzierbar.
- Monotonieverhalten : für x > 0 steigend, für x < 0 fallend.
- Symmetrie : achsensymmetrisch zur y-Achse.
-
Definitions
– und Wertemenge
:
und 
-
Grenzwerte
: auf beiden Seiten
Terme vereinfachen
Wenn du einen Betrag ausrechnen willst, musst du oft auch Terme vereinfachen. Du bist dir nicht mehr sicher, wie das geht? Dann schau dir hier unser Video dazu an.
