Energieerhaltungssatz
Was ist der Energieerhaltungssatz und was bedeutet er für die verschiedenen Energieformen? Das erfährst du in unserem Video und im Beitrag.
Inhaltsübersicht
Was besagt der Energieerhaltungssatz?
Der Energieerhaltungssatz besagt, dass in einem abgeschlossenen, reibungsfreien System die Summe aller Energien immer gleich bleibt. Bei der Energie handelt es sich also um eine Erhaltungsgröße.
Ein abgeschlossenes System kannst du dir als einen Kasten vorstellen, der keine Energie hinein oder hinaus lässt. Das heißt, die Gesamtenergie im Kasten bleibt immer gleich, weil keine Energie vernichtet oder erzeugt werden kann. Die verschiedenen Energieformen können sich nur in eine andere Form umwandeln.
Zwei bedeutende Energieformen, die dir auch ständig im Alltag begegnen, sind die Bewegungsenergie (kinetische Energie) und die Lageenergie oder auch Höhenenergie (potenzielle Energie). Im Bereich der Mechanik gibt es noch die Spannenergie, die zum Beispiel in einer gespannten Feder steckt.
Energieerhaltungssatz der Mechanik
In der Mechanik umfasst der Energieerhaltungssatz und seine Formel speziell die mechanischen Energieformen. In einem abgeschlossenen System bleibt die gesamte mechanische Energie erhalten:
![Rendered by QuickLaTeX.com \[E_\text{ges} = \textcolor{blue}{E_\text{kin}} + \textcolor{olive}{E_\text{pot}} + \textcolor{magenta}{E_\text{spann}} = \text{konstant}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-52d259cfb527ca0e880ceac4e143f071_l3.png)
Die drei wichtigsten Energieformen sind die kinetische Energie (Bewegungsenergie, Ekin), die potenzielle Energie (Lageenergie, Epot) und die Spannenergie (ESpann, z. B. beim Spannen einer Feder). In unserer Tabelle kannst du die entsprechenden Formeln für die Berechnung der Energieformen sehen.
| Energieform | Formel |
| kinetische Energie |  |
| potenzielle Energie |  |
| Spannenergie | 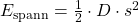 |
Die Formeln kannst du auch in den Energieerhaltungssatz einsetzen. Dann gilt für die Veränderung der Energieformen von einem Zustand 1 in einen Zustand 2:
![Rendered by QuickLaTeX.com \[\textcolor{blue}{\frac{1}{2} \cdot m \cdot v_1\,^2} + \textcolor{olive}{m \cdot g \cdot h_1} + \textcolor{magenta}{\frac{1}{2} \cdot D \cdot s_1\,^2} = \textcolor{blue}{\frac{1}{2} \cdot m \cdot v_2\,^2} + \textcolor{olive}{m \cdot g \cdot h_2} + \textcolor{magenta}{\frac{1}{2} \cdot D \cdot s_2\,^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4192ff37338224bd3f367a173aba7c9b_l3.png)
Wenn sich also eine Größe (z. B. die Höhe h) verändert, wirkt sich das auf eine andere Größe (z. B. die Geschwindigkeit v) genau gegenteilig aus. Eine Energie nimmt ab, während eine andere Energie zunimmt. So bleibt die Gesamtenergie erhalten.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel Fadenpendel
Bei der Schwingung eines Fadenpendels kannst du das Prinzip der Energieerhaltung anschaulich nachvollziehen. Es werden laufend Energien ineinander umgewandelt. Genauer gesagt betrifft das die kinetische und die potenzielle Energie. Nach dem Energieerhaltungssatz geht dabei keine Energie verloren und die Gesamtenergie bleibt erhalten.
Du kannst dir die Energieumwandlung bei einer Schwingung dann so vorstellen:
- Am Punkt der maximalen Auslenkung ist die potenzielle Energie aufgrund der Lage des Pendels am höchsten.
- Wenn der Körper dann den Punkt der Ruheposition durchschwingt, besitzt er die höchste Geschwindigkeit und die kinetische Energie ist am größten. Hier ist die potenzielle Energie dafür aber gleich null.
- Bis der Pendelkörper wieder an der maximalen Auslenkung angekommen ist, wandelt sich die hohe kinetische Energie wieder in potenzielle Energie um.
Du siehst also, dass sich an der Gesamtenergie nichts ändert. Die beiden Energieformen wandeln sich immer entsprechend gegenteilig um.
Energieerhaltungssatz Formel
Den Energieerhaltungssatz kannst du für alle Energieformen ausdrücken und nicht nur für mechanische Energien. Dazu zählt zum Beispiel elektrische Energie oder Wärme. Die allgemeine Formel für die Energieerhaltung lautet dann:
![Rendered by QuickLaTeX.com \[E_\text{ges} = E_1 + E_2 + E_3 + ... = \text{konstant}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-015f6866a1ad1500f90b5d5f5c6a1173_l3.png)
Der Anteil der Energieformen (E1, E2, E3, etc.) an der Gesamtenergie (Eges) kann sich also beliebig ändern, die Gesamtenergie bleibt aber immer dieselbe (= Erhaltungsgröße).
Die Einheit der Energie ist das Joule (bzw. das Newtonmeter):
![Rendered by QuickLaTeX.com \[[E] = 1\,\text{J} = 1\,\frac{\text{kg} \cdot \text{m}^2}{\text{s}^2} = 1\,\text{Nm}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1dbca58e36874fb3121ff367c384c45e_l3.png)
Energieerhaltung Beispiele
Der Energieerhaltungssatz kann für sämtliche Energieformen angewendet werden. In der Natur gibt es sehr viele verschiedene Energieformen. Zu den Wichtigsten gehören:
- kinetische Energie (Bewegungsenergie)
- potenzielle Energie (Lageenergie)
- thermische Energie (Wärmeenergie)
- chemische Energie
- elektrische Energie
- Strahlungsenergie (Lichtenergie)
Oft macht es den Eindruck, dass in einer Umwandlung Energie verloren geht. Tatsächlich wird die Energie aber in eine Energieform umgewandelt, die schwer oder gar nicht nutzbar ist, zum Beispiel Wärme. Schauen wir uns dazu Beispiele an:
Beispiel 1: Die Glühbirne
- Die elektrische Energie in einer Glühbirne wird nicht vollständig in Strahlungsenergie bzw. Licht umgewandelt.
- Ein gewisser Teil der Energie wird auch in Form von Wärme an die Umgebung abgegeben.
- Dabei gilt: elektrische Energie = Wärmeenergie + Strahlungsenergie.
Beispiel 2: Das bremsende Auto
- Wenn ein fahrendes Auto abbremst, verringert sich dabei seine Bewegungsenergie bzw. kinetische Energie.
- Zusätzlich erhitzen sich aber auch die Bremsen des Autos und die thermische Energie nimmt zu.
- Es gilt: Die Summe von kinetischer Energie und Wärmeenergie ist konstant.
Beispiel 3: Der Automotor
- Bei einem Motor wird durch die Verbrennung von Benzin chemische Energie frei, die zum Teil in kinetische Energie umgewandelt wird.
- Ein Großteil der Energie geht jedoch als Wärmeenergie an die Umgebung „verloren“.
- Auch hier erkennst du: Wärmeenergie + Bewegungsenergie = Chemische Energie des Benzins.
Geschlossenes und offenes System
Der Energieerhaltungssatz gilt nur für abgeschlossene Systeme. Das liegt vor allem daran, dass bei offenen Systemen eine Energiezunahme oder -abnahme stattfinden kann. Abgeschlossen bedeutet, dass keine äußeren Kräfte auf das System einwirken.
Du kannst dir das ganz gut mit einem Kasten als System vorstellen. Wenn der Kasten geschlossen ist, hast du ein abgeschlossenes System. Keine neue Energie kann rein und keine bestehende Energie kann raus. Außerdem wirken auf den Kasten auch keine äußeren Kräfte mehr, denn sie sind schon im System, dem Kasten, mit berücksichtigt. Der Energieerhaltungssatz ist gültig.
Wenn der Kasten aber offen ist, kannst du von einem offenen System sprechen. Die Energie innerhalb des Kastens kann sowohl mehr als auch weniger werden. Manche äußeren Kräfte wurden hier im System, dem Kasten, nicht berücksichtigt und so kann es zu einer Änderung der Energie darin kommen. Du kannst den Energieerhaltungssatz nicht anwenden.
Spezialfälle des Energieerhaltungssatzes
Grundsätzlich kannst du den Energieerhaltungssatz für jeden beliebigen Vorgang in abgeschlossenen Systemen anwenden. Manchmal beobachtest du dabei allerdings Vorgänge, bei denen nur bestimmte Energieformen wichtig sind. Es handelt sich um Spezialfälle des Energieerhaltungssatzes.
Im Folgenden betrachten wir neben dem bereits angesprochenen Energieerhaltungssatz der Mechanik zwei weitere wichtige Spezialfälle:
- Erster Hauptsatz der Wärmelehre: Er befasst sich mit dem Zusammenhang von innerer Energie U, Wärmemenge Q und mechanischer Arbeit W und wie sie sich zueinander verhalten. Dabei sagt er auch aus, dass die Energien ineinander umwandelbar sind, aber nicht erzeugt oder vernichtet werden können.
- Lenzsches Gesetz: Es befasst sich mit dem Verhalten der Energie bei elektromagnetischen Induktionen . Hierbei kann ebenfalls der Energieerhaltungssatz angewendet werden.
Übung: Energieerhaltungssatz anwenden
Wie du den Energieerhaltungssatz anwenden kannst, schauen wir uns anhand eines Beispiels aus der Mechanik an. Dabei nehmen wir an, dass uns vom Balkon aus dem dritten Stock (7,5 Meter) ein Blumentopf mit einem Gewicht von 3 kg herunter fällt.
Mit welcher Geschwindigkeit v wird der Blumentopf aufschlagen?
- Zuerst können wir die potenzielle Energie
 berechnen, indem wir die Masse m mit der Höhe h und der Fallbeschleunigung g (auf der Erde beträgt sie etwa 9,81 m/s2) multiplizieren:
berechnen, indem wir die Masse m mit der Höhe h und der Fallbeschleunigung g (auf der Erde beträgt sie etwa 9,81 m/s2) multiplizieren:
![Rendered by QuickLaTeX.com \[E_\text{pot} = m \cdot g \cdot h = 3\,\text{kg} \cdot 9,81\frac{\text{m}}{\text{s}^2} \cdot 7,5\,\text{m} = 220,725\,\text{J}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d7a8e9a59ee3b3f9c415582d69643636_l3.png)
- Wir erhalten 220,725 Joule. Wenn wir davon ausgehen, dass die gesamte potenzielle Energie in kinetische Energie umgewandelt werden kann, dann können wir beide Energien gleichsetzen.
![Rendered by QuickLaTeX.com \[E_\text{pot} = E_\text{kin} = \frac{1}{2} \cdot m \cdot v^2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-66e54306e1078d6b0cf789af7397a5b4_l3.png)
- Nun nehmen wir die Formel für die kinetische Energie und setzen die Masse sowie den Wert für die potenzielle Energie ein. Anschließend formen wir nach der Geschwindigkeit um und ziehen die Wurzel.
![Rendered by QuickLaTeX.com \[220,725\,\text{J} = \frac{1}{2} \cdot 3\,\text{kg} \cdot v^2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b23cb4c2235bbabfc844da78cd77c8e2_l3.png)
![Rendered by QuickLaTeX.com \[v^2 = 147,15\,\frac{\text{J}}{\text{kg}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ef381882277868cf458fae155c8ae139_l3.png)
![Rendered by QuickLaTeX.com \[v = 12,13\,\frac{\text{m}}{\text{s}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-12c0a605ba2614839e75d540cf08c76e_l3.png)
Die gesuchte Geschwindigkeit beträgt also 12,13 Meter pro Sekunde.
Letztendlich konntest du die Geschwindigkeit also nur berechnen, weil die potenzielle Energie vollständig in kinetische Energie umgewandelt wurde. Ein solcher Vorgang ist die Grundvoraussetzung für die Energieerhaltung. Wenn du jetzt noch mehr über die Energieumwandlung wissen möchtest, schau dir unser Video dazu an. Bis gleich!

