Extremwertaufgaben
In diesem Artikel wird gezeigt, wie Extremwertaufgaben mit und ohne Nebenbedingung gelöst werden können – auch für mehrdimensionale Extremwertprobleme. Es werden zudem zu den verschiedenen Fällen Beispiele mit Lösungen präsentiert.
Ist dir das alles zu viel? Dann ist unser Video , in dem wir das Wichtigste in weniger als 5 Minuten zusammengefasst haben, genau das Richtige für dich!
Inhaltsübersicht
Extremwertaufgaben Definition
Zur Lösung der Extremwertaufgabe wird die Größe als Funktion dieser Variablen beschrieben und deren Extremstellen ermittelt.
Häufig ist anstelle von Extremwertaufgaben auch die Rede von Optimierungsaufgaben. Ebenso geläufig sind die Bezeichnungen als Extremwertprobleme, Extremalprobleme oder Extremalaufgaben.
Extremwertaufgaben lösen: Vorgehensweise
Formuliert man die Abhängigkeit der zu optimierenden Größe von den Variablen auf mathematische Art und Weise, so erhält man eine Funktion. Für diese Funktion gilt es dann die Maxima bzw. die Minima, also die Extremstellen, zu bestimmen. Dies gleicht dann einer typischen Aufgabe aus dem Bereich der Kurvendiskussion. Im Folgenden soll nun Schritt für Schritt das Vorgehen zur Lösung von Extremwertaufgaben beschrieben werden.
Dabei sollen zunächst Größen betrachtet werden, die von nur einer Variablen abhängen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Ableiten und Extrema bestimmen
Für die Funktion  gilt es nun die Extrema zu bestimmen. Ein Extremum kann nur an Stellen vorliegen, an denen die erste Ableitung
der Funktion Null ist:
gilt es nun die Extrema zu bestimmen. Ein Extremum kann nur an Stellen vorliegen, an denen die erste Ableitung
der Funktion Null ist:

Um diese Stellen zu finden, wird die Ableitungsfunktion  berechnet und deren Nullstellen bestimmt. Jede Stelle, die dieses Kriterium erfüllt, nennt man „kritische Stelle“. An diesen kritischen Stellen muss nun noch der Wert der zweiten Ableitung bestimmt werden. Ist er positiv, so handelt es sich bei der kritischen Stelle um ein Minimum. Falls er negativ ist, befindet sich an der kritischen Stelle ein Maximum.
berechnet und deren Nullstellen bestimmt. Jede Stelle, die dieses Kriterium erfüllt, nennt man „kritische Stelle“. An diesen kritischen Stellen muss nun noch der Wert der zweiten Ableitung bestimmt werden. Ist er positiv, so handelt es sich bei der kritischen Stelle um ein Minimum. Falls er negativ ist, befindet sich an der kritischen Stelle ein Maximum.
Extremwertaufgaben mit Nebenbedingungen
Bei vielen Extremwertproblemen hängt die zu optimierende Größe allerdings nicht nur von einer, sondern von zwei Variablen ab und an diese Variablen wird eine Bedingung geknüpft, welche „Nebenbedingung“ genannt wird. Wie solche Aufgaben gelöst werden wird nun gezeigt.
Zielfunktion aufstellen
Zunächst einmal wird die in der Extremwertaufgabe zu maximierende bzw. zu minimierende Größe als Funktion der Variablen formuliert, von denen sie abhängt. Sind diese Variablen  und
und  , während die Größe selbst mit
, während die Größe selbst mit  abgekürzt wird, so muss also die Funktion
abgekürzt wird, so muss also die Funktion  bestimmt werden.
bestimmt werden.
Nebenbedingung formulieren und umstellen
Nun muss die Nebenbedingung, welche an die Variablen  und
und  gestellt wird in einer mathematischen Gleichung formuliert werden. Anschließend wird diese Gleichung nach einer Variablen umgestellt, sodass man eine Funktion
gestellt wird in einer mathematischen Gleichung formuliert werden. Anschließend wird diese Gleichung nach einer Variablen umgestellt, sodass man eine Funktion  oder
oder  erhält.
erhält.
Extremalfunktion aufstellen
Die so erhaltene Funktion lässt sich nun in  einsetzen und man erhält eine Funktion, die die Größe
einsetzen und man erhält eine Funktion, die die Größe  in Abhängigkeit nur noch einer Variablen beschreibt:
in Abhängigkeit nur noch einer Variablen beschreibt:
 oder
oder 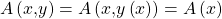
Diese Funktion kann nun auf bereits beschriebene Art und Weise auf Extrema überprüft werden.
Extremwertaufgaben mit Lösung
Im Folgenden soll anhand zweier Extremwertaufgaben das beschriebene Vorgehen dargelegt werden.
Beispiel 1: Extremwertaufgaben
Im ersten Extremwertproblem wird der Graph der Funktion  betrachtet. Zwischen diesem Graphen und der
betrachtet. Zwischen diesem Graphen und der  -Achse soll ein Rechteck so einbeschrieben werden, dass sich zwei Punkte des Rechtecks auf der
-Achse soll ein Rechteck so einbeschrieben werden, dass sich zwei Punkte des Rechtecks auf der  -Achse befinden und die anderen beiden auf dem Graphen. Für dieses Rechteck soll die Position der Punkte auf der
-Achse befinden und die anderen beiden auf dem Graphen. Für dieses Rechteck soll die Position der Punkte auf der  -Achse so bestimmt werden, dass der Flächeninhalt des Rechtecks maximal wird.
-Achse so bestimmt werden, dass der Flächeninhalt des Rechtecks maximal wird.
Die zu maximierende Größe ist also der Flächeninhalt des Rechtecks. Liegen die Punkte des Rechtecks auf der  -Achse bei
-Achse bei  und
und  , so ist die Länge des Rechtecks gleich
, so ist die Länge des Rechtecks gleich  . Dessen Breite entspricht dann dem Funktionswert von
. Dessen Breite entspricht dann dem Funktionswert von  an der Stelle
an der Stelle  . Der Flächeninhalt
. Der Flächeninhalt  des Rechtecks, welcher die zu maximierende Größe ist, wird also durch folgende Funktion beschrieben:
des Rechtecks, welcher die zu maximierende Größe ist, wird also durch folgende Funktion beschrieben:

Der zweite Schritt ist nun diese Funktion abzuleiten und deren Extremstellen zu bestimmen. Die Ableitungsfunktion lautet:

Die kritischen Stellen sind genau die Nullstellen dieser Funktion, welche sich mithilfe der Mitternachtsformel berechnen lassen. Sie lauten: 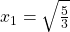 und
und 
Nun lässt sich die zweite Ableitung der Flächeninhaltsfunktion an diesen beiden kritischen Stellen betrachten. Sie lautet:

Setzt man die beiden kritischen Stellen in diese Funktion ein, so sieht man, dass die zweite Ableitung an der kritischen Stelle  negativ und an der kritischen Stelle
negativ und an der kritischen Stelle  positiv ist. Das bedeutet, dass bei
positiv ist. Das bedeutet, dass bei  ein Maximum der Funktion und bei
ein Maximum der Funktion und bei  ein Minimum der Funktion vorliegt. Das Rechteck hat also den maximalen Flächeninhalt, wenn die Punkte auf der
ein Minimum der Funktion vorliegt. Das Rechteck hat also den maximalen Flächeninhalt, wenn die Punkte auf der  -Achse bei
-Achse bei 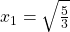 und
und  liegen. Für die komplette Lösung der Extremwertaufgabe kann noch der zugehörige Flächeninhalt berechnet werden:
liegen. Für die komplette Lösung der Extremwertaufgabe kann noch der zugehörige Flächeninhalt berechnet werden:

Beispiel 2: Extremwertaufgaben
In dieser Extremwertaufgabe soll mit einem 50 Meter langen Maschendrahtzaun ein Rechteck mit maximalem Flächeninhalt abgesteckt werden. Die zu maximierende Größe ist also der Flächeninhalt  eines Rechtecks. Zunächst soll dieser als Funktion der Variablen geschrieben werden, von denen er abhängt. Dies sind die Länge
eines Rechtecks. Zunächst soll dieser als Funktion der Variablen geschrieben werden, von denen er abhängt. Dies sind die Länge  und die Breite
und die Breite  des Rechtecks und dessen Flächeninhalt berechnet sich zu:
des Rechtecks und dessen Flächeninhalt berechnet sich zu:

Nun gilt es die Nebenbedingung zu formulieren, welche an die beiden Variablen geknüpft ist. Es ist bekannt, dass der Umfang  des Rechtecks 50 Meter betragen soll:
des Rechtecks 50 Meter betragen soll:
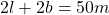
Diese Nebenbedingung kann nun nach einer der Variablen umgestellt werden:

Diese Funktion  kann nun in
kann nun in  eingesetzt werden und man erhält:
eingesetzt werden und man erhält:

Für die Funktion  können nun die kritischen Stellen mithilfe der ersten Ableitungsfunktion
können nun die kritischen Stellen mithilfe der ersten Ableitungsfunktion  bestimmt werden:
bestimmt werden:

Diese ist nur an der Stelle  gleich Null. Das bedeutet, dass dies die einzige kritische Stelle der Funktion ist. Da die zweite Ableitung
gleich Null. Das bedeutet, dass dies die einzige kritische Stelle der Funktion ist. Da die zweite Ableitung  an dieser Stelle negativ ist, befindet sich dort ein Maximum der Funktion. Das bedeutet also, dass der Flächeninhalt für eine Breite des Rechtecks von 12,5 m maximal ist.
an dieser Stelle negativ ist, befindet sich dort ein Maximum der Funktion. Das bedeutet also, dass der Flächeninhalt für eine Breite des Rechtecks von 12,5 m maximal ist.
Mehrdimensionale Extremstellen berechnen
Bei mehrdimensionalen Extremwertaufgaben sollen die Extremstellen einer Funktion  bestimmt werden, die von mehreren Variablen
bestimmt werden, die von mehreren Variablen  abhängt. Hier sieht das Vorgehen ähnlich aus wie für Funktionen einer Variablen: Es werden die kritischen Stellen mithilfe der ersten Ableitung bzw. dem Gradienten
bestimmt und das Krümmungsverhalten an diesen Stellen mithilfe der zweiten Ableitung bzw. der Hesse-Matrix
untersucht.
abhängt. Hier sieht das Vorgehen ähnlich aus wie für Funktionen einer Variablen: Es werden die kritischen Stellen mithilfe der ersten Ableitung bzw. dem Gradienten
bestimmt und das Krümmungsverhalten an diesen Stellen mithilfe der zweiten Ableitung bzw. der Hesse-Matrix
untersucht.
Gradient berechnen
Um die kritischen Stellen zu ermitteln, wird die erste Ableitung bzw. der Gradient  der Funktion
der Funktion  berechnet. Die kritischen Stellen der Funktion sind genau diejenigen Stellen, an denen dieser verschwindet:
berechnet. Die kritischen Stellen der Funktion sind genau diejenigen Stellen, an denen dieser verschwindet:

Hesse Matrix bestimmen
Um das Krümmungsverhalten der Funktion an den kritischen Stellen ermitteln zu können, wird die Hesse-Matrix benötigt. Zu ihrer Berechnung müssen sämtliche partielle Ableitungen zweiter Ordnung bestimmt werden und in Matrixschreibweise folgendermaßen angeordnet werden:

Definitheit der Hesse Matrix bestimmen
Zuletzt werden nacheinander die kritischen Stellen in die Matrix eingesetzt und diese anschließend auf Definitheit überprüft. Die Matrix…
- …ist genau dann positiv (negativ) definit, wenn alle ihre Eigenwerte positiv (negativ) sind.
- …ist genau dann positiv (negativ) semidefinit, wenn alle ihre Eigenwerte
 (
( ) sind.
) sind. - …ist genau dann indefinit, wenn sie mindestens einen positiven und einen negativen Eigenwert besitzt.
Kennt man die Definitheit der Hesse-Matrix an den kritischen Stellen, so lassen diese sich wie folgt klassifizieren:
- Ist die Hesse-Matrix an einer kritischen Stelle positiv definit, dann ist dort ein lokales Minimum der Funktion.
- Ist die Hesse-Matrix an einer kritischen Stelle negativ definit, dann ist dort ein lokales Maximum der Funktion.
- Ist die Hesse-Matrix an einer kritischen Stelle indefinit, dann ist dort ein Sattelpunkt der Funktion.
- Ist die Hesse-Matrix an einer kritischen Stelle semidefinit, so kann auf diese Art und Weise der Charakter der Extremstelle nicht ermittelt werden.
Mehrdimensionale Extremwertaufgaben Übungen
Im Folgenden soll anhand zweier Extremwertaufgaben eingeübt werden, wie Extremstellen im Mehrdimensionalen bestimmt werden können.
Beispiel 1: Mehrdimensionale Extremwertaufgaben
In dieser Extremwertaufgabe soll die Funktion 
auf Extrema untersucht werden. Dazu werden die einzelnen oben beschriebenen Schritte abgearbeitet. Zunächst wird der Gradient der Funktion bestimmt:

Die kritischen Stellen der Funktion ergeben sich als Nullstellen dieses Gradienten. Dieser verschwindet genau dann, wenn  und
und  gelten. Das heißt die einzige kritische Stelle ist
gelten. Das heißt die einzige kritische Stelle ist  .
.
Nun kann mithilfe der Hesse-Matrix überprüft werden, ob es sich bei dieser Stelle um ein Minimum, Maximum oder einen Sattelpunkt handelt. Dazu wird diese zunächst einmal berechnet. Sie lautet:

Nun muss die Definitheit der Hesse-Matrix an der kritischen Stelle untersucht werden. Dazu werden die Eigenwerte der Hesse-Matrix bestimmt, welche die Nullstellen des charakteristischen Polynoms \chi_{\left(Hess\ f\right)\left(x,y\right)}=\left(\lambda-2\right)^2 darstellen. Da  die einzige Nullstelle dieses Polynoms ist und diese positiv ist, ist die Hesse-Matrix an jeder Stelle und insbesondere an der kritischen Stelle
die einzige Nullstelle dieses Polynoms ist und diese positiv ist, ist die Hesse-Matrix an jeder Stelle und insbesondere an der kritischen Stelle  positiv definit. Das bedeutet also, dass die Funktion
positiv definit. Das bedeutet also, dass die Funktion  an dieser Stelle ein Minimum besitzt.
an dieser Stelle ein Minimum besitzt.
Beispiel 2: Mehrdimensionale Extremwertaufgaben
In dieser Extremwertaufgabe sollen die Extremstellen der Funktion  bestimmt werden. Der Gradient der Funktion lautet
bestimmt werden. Der Gradient der Funktion lautet  und dieser ist nur an den Stellen
und dieser ist nur an den Stellen  und
und  gleich Null.
gleich Null.
Das sind also die einzigen kritischen Stellen der Funktion und an diesen muss die Definitheit der Hesse-Matrix überprüft werden. Die Hesse-Matrix lautet allgemein:

An den beiden kritischen Stellen  und
und  ergibt sich:
ergibt sich:


Beide Matrizen besitzen dasselbe charakteristischen Polynom:

Dieses Polynom besitzt die beiden Nullstellen  und
und  . Die Hesse-Matrix besitzt also in beiden Fällen einen positiven und einen negativen Eigenwert, was bedeutet, dass sie indefinit ist. Somit stellen die beiden kritischen Stellen
. Die Hesse-Matrix besitzt also in beiden Fällen einen positiven und einen negativen Eigenwert, was bedeutet, dass sie indefinit ist. Somit stellen die beiden kritischen Stellen  und
und  Sattelpunkte der Funktion
Sattelpunkte der Funktion  dar.
dar.
Mehrdimensionale Extremwertaufgaben mit Nebenbedingung
Auch für Funktionen mehrerer Variablen können Extremwertaufgaben mit Nebenbedingung formuliert werden. Diese lassen sich manchmal auf elementare Weise durch Umstellen der Nebenbedingung und Einsetzen in die Funktion lösen. In den anderen Fällen führt das Lagrange-Verfahren ans Ziel.
