Wie erkenne ich schnell am Skalarprodukt, ob der Winkel zwischen zwei Vektoren spitz oder stumpf ist?

Am Vorzeichen des Skalarprodukts erkennst du die Winkelart sofort. Gilt , ist der Winkel spitz, bei ist er genau , und bei ist der Winkel stumpf. Das kommt von .

Welche typischen Rechenfehler passieren beim Skalarprodukt am häufigsten?

Häufig passieren Vorzeichenfehler und „falsche Paare“ bei den Komponenten. Du multiplizierst immer nur gleiche Positionen, also , usw., und addierst erst danach. Achte besonders auf Klammern bei negativen Zahlen, z. B. .

Wie rechne ich den Winkel aus, wenn ich mit dem Taschenrechner wegen Rundungen größer als 1 bekomme?

Wenn durch Rundungen z. B. herauskommt, ersetzt du den Wert durch 1 (oder bei durch −1). Denn mathematisch muss immer zwischen −1 und 1 liegen. Danach kannst du sicher berechnen.

Wie unterscheide ich das Skalarprodukt vom Kreuzprodukt, wenn ich in Aufgaben nur „Produkt“ lese?

Beim Skalarprodukt ist das Ergebnis immer eine Zahl und du nutzt es oft für Winkel, Orthogonalität und Längen. Beim Kreuzprodukt ist das Ergebnis ein Vektor, der senkrecht auf beiden Ausgangsvektoren steht, und es geht meist um Flächen oder Normalenvektoren. Außerdem ist das Kreuzprodukt nur in (typisch Schulkontext) definiert.

Video

Quiz

Hier geht's zum Video „Betrag eines Vektors“

Hier geht's zum Video „Winkel zwischen zwei Vektoren“

Hier geht's zum Video „Betrag eines Vektors“

Hier geht's zum Video „Winkel zwischen zwei Vektoren“

Skalarprodukt

Wichtige Inhalte in diesem Video

Skalarprodukt einfach erklärt

(00:12)

Skalarprodukt berechnen

(01:09)

Rechter Winkel zwischen den Vektoren

(02:15)

Länge eines Vektors

(02:37)

Winkel zwischen den Vektoren

(03:09)

Du möchtest wissen, was das Skalarprodukt ist und wie du es berechnest? Hier und im Video erklären wir es dir Schritt für Schritt!

Inhaltsübersicht

Skalarprodukt einfach erklärt

im Videozur Stelle im Video springen

(00:12)

Das Skalarprodukt ist ein Produkt aus zwei Vektoren $\vec{a}$ und $\vec{b}$ . Um es zu bilden, multiplizierst du die einzelnen Komponenten der Vektoren miteinander. Anschließend addierst du die Produkte.

$\vec{a} \circ \vec{b} =\left(\begin{array}{c} \textcolor{blue}{a_1} \\ \textcolor{magenta}{a_2} \\ \textcolor{teal}{a_3}\end{array}\right) \circ \left(\begin{array}{c} \textcolor{blue}{b_1} \\ \textcolor{magenta}{b_2} \\ \textcolor{teal}{b_3} \end{array}\right) = \textcolor{blue}{a_1} \cdot \textcolor{blue}{b_1} + \textcolor{magenta}{a_2} \cdot \textcolor{magenta}{b_2} + \textcolor{teal}{a_3} \cdot \textcolor{teal}{b_3}$

Das Ergebnis ist eine reelle Zahl — auch Skalar genannt. Wichtig ist, dass du das Skalarprodukt nur mit gleich großen Vektoren berechnen kannst. Beide Vektoren müssen also dieselbe Anzahl an Komponenten haben.

Übrigens: Für das Skalarprodukt gibt es verschiedene Schreibweisen: $\vec{a} \circ \vec{b}$ , $\vec{a} \cdot \vec{b}$ , $<\vec{a},\vec{b}>$

Skalarprodukt berechnen

im Videozur Stelle im Video springen

(01:09)

Schauen wir uns an ein paar Beispielen an, wie du das Skalarprodukt der zwei Vektoren $\vec{a}$ und $\vec{b}$ berechnest.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Skalarprodukt — Zwei Komponenten

Vektoren in der Ebene bestehen immer aus nur zwei Komponenten. Beispielsweise hast du folgende Vektoren gegeben:

$\vec{a} = \left(\begin{array}{c} \textcolor{blue}{-2} \\ \textcolor{magenta}{-1} \end{array}\right)$ ,

$\vec{b} = \left(\begin{array}{c} \textcolor{blue}{3} \\ \textcolor{magenta}{0} \end{array}\right)$

Um das Skalarprodukt $\vec{a} \circ \vec{b}$ zu bilden, multiplizierst du zuerst die beiden Vektoren komponentenweise miteinander:

$\textcolor{blue}{a_1} \cdot \textcolor{blue}{b_1} = (-2) \cdot 3 = -6$ ,

$\textcolor{magenta}{a_2} \cdot \textcolor{magenta}{b_2} = (-1) \cdot 0 = 0$

Anschließend addierst du die Produkte: (-6) + 0 = -6

Das Skalarprodukt von $\vec{a}$ und $\vec{b}$ beträgt also -6.

Skalarprodukt — Drei Komponenten

Im Raum besitzen Vektoren drei Komponenten. Die Vektoren $\vec{a}$ und $\vec{b}$ sehen jetzt z. B. so aus:

$\vec{a} = \left(\begin{array}{c} \textcolor{blue}{-1} \\ \textcolor{magenta}{3} \\ \textcolor{teal}{0,5} \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} \textcolor{blue}{2} \\ \textcolor{magenta}{-1,5} \\ \textcolor{teal}{-1} \end{array}\right)$

Die Berechnung bleibt aber dieselbe. Du multiplizierst jeweils die Komponenten und addierst schließlich die Produkte:

$\begin{align*} \vec{a} \circ \vec{b} &= \left(\begin{array}{c} \textcolor{blue}{-1} \\ \textcolor{magenta}{3} \\ \textcolor{teal}{0,5} \end{array}\right) \circ \left(\begin{array}{c} \textcolor{blue}{2} \\ \textcolor{magenta}{-1,5} \\ \textcolor{teal}{-1} \end{array}\right) \\ &= \textcolor{blue}{(-1)} \cdot \textcolor{blue}{2} + \textcolor{magenta}{3} \cdot \textcolor{magenta}{(-1,5)} + \textcolor{teal}{0,5} \cdot \textcolor{teal}{(-1)} \\ &= \textcolor{blue}{(-2)} + \textcolor{magenta}{(-4,5)} + \textcolor{teal}{(-0,5)} = -7 \\ \end{align*}$

Auch hier ist das Skalarprodukt eine reelle Zahl, nämlich -7.

Skalarprodukt Vektoren — Verwendung

Mit dem Skalarprodukt kannst du verschiedene Eigenschaften über Vektoren herausfinden. Zum Beispiel, in welchem Winkel die Vektoren zueinander stehen oder wie lang ein Vektor ist. Im Folgenden schauen wir uns das einmal genauer an.

Rechter Winkel zwischen den Vektoren

im Videozur Stelle im Video springen

(02:15)

Ist das Skalarprodukt von zwei Vektoren gleich 0, sind sie orthogonal zueinander. Das heißt, sie bilden zusammen einen rechten Winkel (90°). Es gilt also:

$\vec{a} \circ \vec{b} = 0$ → $\vec{a} \perp \vec{b}$

Zum Beispiel hast du folgende Vektoren:

$\vec{a} = \left(\begin{array}{c} \textcolor{blue}{-2} \\ \textcolor{magenta}{6} \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} \textcolor{blue}{3} \\ \textcolor{magenta}{1} \end{array}\right)$

Das Skalarprodukt von beiden Vektoren sieht so aus:

$\vec{a} \circ \vec{b} = \left(\begin{array}{c} \textcolor{blue}{-2} \\ \textcolor{magenta}{6} \end{array}\right) \circ\left(\begin{array}{c} \textcolor{blue}{3} \\ \textcolor{magenta}{1} \end{array}\right) = \textcolor{blue}{(-2)} \cdot \textcolor{blue}{3} + \textcolor{magenta}{6} \cdot \textcolor{magenta}{1} = (-6) + 6 = 0$

Da der Skalar 0 ist, sind es zueinander orthogonale Vektoren.

Länge eines Vektors

im Videozur Stelle im Video springen

(02:37)

Mit dem Skalarprodukt kannst du auch die Länge eines Vektors bestimmen. Denn für die Länge eines Vektors gilt:

Zwei Komponenten: $|\vec{a}| = \sqrt{\vec{a} \cdot \vec{a}} = \sqrt{a_1^2 + a_2^2}$
Drei Komponenten: $|\vec{a}| = \sqrt{\vec{a} \cdot \vec{a}} = \sqrt{a_1^2 + a_2^2 + a_3^2}$

Um also die Länge des Vektors $\vec{a}$ zu berechnen, bildest du das Skalarprodukt aus dem Vektor mit sich selbst. Anschließend ziehst du daraus die Wurzel.

Beispielsweise hast du den Vektor $\vec{a} = \left(\begin{array}{c} \textcolor{blue}{3} \\ \textcolor{magenta}{4} \\ \textcolor{teal}{-2} \end{array}\right)$

Dafür berechnest du als Erstes das Skalarprodukt:

$\vec{a} \circ \vec{a} = \textcolor{blue}{3} \cdot \textcolor{blue}{3} + \textcolor{magenta}{4} \cdot \textcolor{magenta}{4} + \textcolor{teal}{(-2)} \cdot \textcolor{teal}{(-2)} = 29$

Nun musst du nur noch die Wurzel ziehen und du bekommst die Länge:

$|\vec{a}| = \sqrt{29} = 5,39$

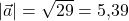
Der Vektor hat also eine Länge von 5,39 LE (Längeneinheiten).

Winkel zwischen den Vektoren

im Videozur Stelle im Video springen

(03:09)

Zwei Vektoren schließen zusammen immer einen Winkel ein. Den kannst du ebenfalls mithilfe des Skalarprodukts berechnen. Für den Winkel zwischen Vektoren gilt nämlich:

$\vec{a} \circ \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos(\theta)$

Das Skalarprodukt entspricht also dem Produkt aus den Längen der Vektoren und dem Cosinus des Winkels, den sie einschließen. Mithilfe der Umkehrfunktion arccos erhältst du den Winkel $\theta$ :

$\cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}$

Mithilfe der Umkehrfunktion arccos erhältst du den Winkel $\theta$ . Dafür nutzt du die „cos^-1“–Taste auf deinem Taschenrechner:

$\theta = \cos^{-1}(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|})$

Wichtig: Der Winkel zwischen zwei Vektoren hat immer einen Wert zwischen 0° und 180°.

Winkel zwischen zwei Vektoren, Skalarprodukt — Winkel zwischen zwei Vektoren

Sieh dir dazu ein Beispiel an:

Du hast die beiden Vektoren $\vec{a} = \left(\begin{array}{c} \textcolor{blue}{4} \\ \textcolor{magenta}{1} \end{array}\right)$ und $\vec{b} = \left(\begin{array}{c} \textcolor{blue}{1} \\ \textcolor{magenta}{-2} \end{array}\right)$

Um den Winkel $\theta$ zu berechnen, bildest du wieder erst das Skalarprodukt der beiden Vektoren:

$\vec{a} \circ \vec{b} = \textcolor{blue}{4} \cdot \textcolor{blue}{1} + \textcolor{magenta}{1} \cdot \textcolor{magenta}{(-2)} = 4 + (-2) = 2.$

Als Nächstes berechnest du die Längen der Vektoren:

$|\vec{a}| = \sqrt{\textcolor{blue}{4^2} + \textcolor{magenta}{1^2}} = \sqrt{17}$

$|\vec{b}| = \sqrt{\textcolor{blue}{1^2} + \textcolor{magenta}{(-2)^2}} = \sqrt{5}.$

Nun setzt du die Werte in die umgeformte Formel ein:

$\cos(\theta) = \frac{2}{ \sqrt{17} \cdot \sqrt{5}} =0,22$

$\theta = \cos^{-1}(0,22) = 77,29^{\circ}$

Tipp: Wenn das Skalarprodukt von $\vec{a}$ und $\vec{b}}$ > 0 ist, handelt es sich um einen spitzen Winkel ( $\theta$ < 90°). Ist $\vec{a} \circle \vec{b}$ hingegen < 0, ist es ein stumpfer Winkel ( $\theta$ > 90°).

Skalarprodukt berechnen — Aufgaben

Du möchtest die Berechnung des Skalarprodukts und seine Verwendungen direkt üben? Dann haben wir hier ein paar Übungsaufgaben mit Lösungen für dich:

Aufgabe 1: Skalarprodukt Vektoren

Überprüfe, ob die folgenden Vektoren senkrecht zueinanderstehen.

a) $\vec{a} = \left(\begin{array}{c} 1 \\ 3 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} -6 \\ 2 \end{array}\right)$

b) $\vec{a} = \left(\begin{array}{c} 4 \\ 1 \\ 6 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} -1 \\ 0 \\ 3 \end{array}\right)$

Lösung Aufgabe 1

a) Um herauszufinden, ob zwei Vektoren senkrecht aufeinander stehen, musst du prüfen, ob das Skalarprodukt null ergibt.

$\vec{a} \circ \vec{b} = 1 \cdot (-6) + 3 \cdot 2 = 0.$

Damit stehen die beiden Vektoren senkrecht aufeinander.

b) Hier gehst du genauso vor wie im vorherigen Fall, nur mit einer Komponente mehr.

$\vec{a} \circ \vec{b} = 4 \cdot (-1) + 1 \cdot 0 + 6 \cdot 3 = 14$

Die Vektoren $\vec{a}$ und $\vec{b}$ sind nicht orthogonal.

Aufgabe 2: Skalarprodukt Winkel

Berechne den Winkel zwischen den Vektoren:

$\vec{a} = \left(\begin{array}{c} 2 \\ -8 \\ -1 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} 8 \\ -3 \\ 5 \end{array}\right)$

Lösung Aufgabe 2

Um den Winkel zu bestimmen, musst du zuerst das Skalarprodukt und die Längen bestimmen. Dann setzt du die Ergebnisse in die entsprechende Formel ein:

$\vec{a} \circ \vec{b} = 2 \cdot 8 + (-8) \cdot (-3) + (-1) \cdot 5 = 35$

$|\vec{a}| = \sqrt{2^2 + (-8)^2 + (-1)^2} = \sqrt{69}$

$|\vec{b}| = \sqrt{8^2 + (-3)^2 + 5^2} = \sqrt{98}$

$\cos(\theta) = \frac{35}{ \sqrt{69} \cdot \sqrt{98}} = 0,43$

$\theta = \cos^{-1}(0,22) = 64,81^{\circ}$

Skalarprodukt — häufigste Fragen

(ausklappen)

Wie erkenne ich schnell am Skalarprodukt, ob der Winkel zwischen zwei Vektoren spitz oder stumpf ist?

Am Vorzeichen des Skalarprodukts erkennst du die Winkelart sofort. Gilt $\vec a\cdot\vec b>0$ , ist der Winkel spitz, bei $\vec a\cdot\vec b=0$ ist er genau $90^\circ$ , und bei $\vec a\cdot\vec b<0$ ist der Winkel stumpf. Das kommt von $\vec a\cdot\vec b=|\vec a||\vec b|\cos(\theta)$ .
Welche typischen Rechenfehler passieren beim Skalarprodukt am häufigsten?

Häufig passieren Vorzeichenfehler und „falsche Paare“ bei den Komponenten. Du multiplizierst immer nur gleiche Positionen, also , usw., und addierst erst danach. Achte besonders auf Klammern bei negativen Zahlen, z. B. $(-3)\cdot(-2)=+6$ .
Wie rechne ich den Winkel aus, wenn ich mit dem Taschenrechner wegen Rundungen $\cos(\theta)$ größer als 1 bekomme?

Wenn durch Rundungen z. B. herauskommt, ersetzt du den Wert durch 1 (oder bei durch −1). Denn mathematisch muss $\frac{\vec a\cdot\vec b}{|\vec a||\vec b|}$ immer zwischen −1 und 1 liegen. Danach kannst du $\theta=\cos^{-1}(\,\cdot\,)$ sicher berechnen.
Wie unterscheide ich das Skalarprodukt vom Kreuzprodukt, wenn ich in Aufgaben nur „Produkt“ lese?

Beim Skalarprodukt ist das Ergebnis immer eine Zahl und du nutzt es oft für Winkel, Orthogonalität und Längen. Beim Kreuzprodukt ist das Ergebnis ein Vektor, der senkrecht auf beiden Ausgangsvektoren steht, und es geht meist um Flächen oder Normalenvektoren. Außerdem ist das Kreuzprodukt nur in $\mathbb R^3$ (typisch Schulkontext) definiert.

Kreuzprodukt/Vektorprodukt

Super, jetzt kennst du dich mit dem Skalarprodukt bestens aus! Eine weitere Art, Vektoren zu multiplizieren, ist das Kreuzprodukt/Vektorprodukt. Hier ist das Ergebnis keine reelle Zahl, sondern ein Vektor. Wie du das Kreuzprodukt berechnest, erklären wir dir hier!