Produktregel
Mit der Produktregel kannst du Funktionen ableiten, die ein Produkt aus mehreren Funktionen sind. Wie das geht, zeigen wir dir hier im Beitrag und im Video!
Inhaltsübersicht
Ableitung Produktregel
Die Produktregel brauchst du bei der Ableitung von Funktionen, die aus einem Produkt bestehen. Dafür zerlegst du deine Funktion f(x) in zwei Teilfunktionen u(x) und v(x).
f(x) = u(x) • v(x)
Beispiel: f(x) = x2 • 4x3
Nun bildest du die Ableitungen u’(x) und v’(x) und setzt sie mit den Funktionen in die Produktregel ein:
f’(x) = u(x) • v’(x) + u’(x) • v(x)
Beispiel: f‘(x) = x2 • 12x2 + 2x • 4x3
Die Produktregel ist dazu da, die Ableitung eines Produktes von Funktionen zu bestimmen. Sie lautet:
f’(x) = u(x) • v’(x) + u’(x) • v(x)
Eine Funktion f(x) = u(x) • v(x) leitest du ab, indem du die erste Funktion mal der Ableitung der zweiten Funktion plus die Ableitung der ersten Funktion mal der zweiten Funktion rechnest.
Beispiel 1: Ganzrationale Funktionen
Leite die Funktion 
ab! Deine Teilfunktionen lauten:
Du kannst die Teilfunktionen wie ganzrationale Funktionen mit der Potenzregel und der Summenregel ableiten.
Setze u, v, u‘ und v‘ in deine Ableitungsregel ein! Danach musst du nur noch ausklammern und vereinfachen.
Die Ableitung von f ist also 60x2+24x. Gar nicht so schwer, oder?
Beispiel 2: Produktregel E-Funktion
Die E-Funktion ist eine besondere Funktion. Denn die Ableitung von ex ist einfach ex. Wenn du eine Funktion ableiten willst, bei der einer der Faktoren eine E-Funktion ist, nutzt du ebenfalls die Produktregel.
Zum Beispiel hast du folgende Funktion: f(x) = (5x – 3) • ex
u(x) = 5x – 3
v(x) = ex
u’(x) = 5
v’(x) = ex
f’(x) = (5x-3) • ex + 5 • ex = ((5x – 3) + 5) • ex = (5x + 2) • ex
Tipp: Besteht der Exponent der E-Funktion aus einer Funktion, musst du die Kettenregel
dafür anwenden. Für die E-Funktion gibt es aber eine Formel, die du immer anwenden kannst: f(x) = eu(x) → f’(x) = u’(x) • eu(x).
Zum Beispiel f(x) = e0,5x-2 → f’(x) = 0,5 • e0,5x-2
Beispiel 3: Sinus und Exponentialfunktion
Schauen wir uns noch ein schwierigeres Beispiel an. Häufig musst du mit der Produktregel auch die Kettenregel anwenden. Berechne deshalb die Ableitung von Funktionen mit trigonometrischen und Exponentialfunktionen!
![\[ f(x) = \sin(2x) \cdot \mathrm{e}^{4x^3} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3f36649b62f40277f2d7cdc34ad3cba7_l3.png "Rendered by QuickLaTeX.com")
Zuerst schreibst du dir wieder deine Teilfunktionen u und v heraus.
Danach musst du die Teilfunktionen ableiten. Fange mit der Teilfunktion u an. Die Ableitung Sinus ist der Cosinus, aber was ist die Ableitung von sin(2x)? Dafür brauchst du die Kettenregel. Sie lautet: g(h(x))‘ = g'(h(x)) • h'(x). Wenn du mit der Kettenregel ableiten musst, berechnest du zuerst die Ableitung der äußeren Funktion g'(x) und multiplizierst sie mit der Ableitung der inneren Funktion h'(x).
Hier ist die Ableitung der äußeren Funktion cos(x) und die Ableitung der inneren Funktion 2x ist gleich 2.
![\[ \textcolor{blue}{u' = (\sin(2x))' = \cos(2x) \cdot 2} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-556e08473a9ac6999ae8bc9397a0919f_l3.png "Rendered by QuickLaTeX.com")
Für die Teilfunktion v leitest du zuerst die e-Funktion ab. Die Ableitung der e-Funktion ist die e-Funktion selbst. Danach musst du das mit der Ableitung der inneren Funktion 4x3 multiplizieren. Die Ableitung der inneren Funktion ist 12x2.
![\[ \textcolor{red}{v' = (\mathrm{e}^{4x^3})' = \mathrm{e}^{4x^3} \cdot 12x^2} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7aaceaa84f7124336f8afe64df3ba6a6_l3.png "Rendered by QuickLaTeX.com")
Setze u, v, u‘ und v‘ in die Produktregel ein!
Wenn du Exponentialfunktionen ableitest, macht Ausklammern deine Ableitung viel leserlicher.
Mit der Produktregel kannst du das Produkt von Funktionen ableiten:
f(x) = u(x) • v(x) ⇒ f'(x) = u(x) • v'(x) + u'(x) • v(x)
Diese Ableitungsregel nennst du auch Leibniz-Regel, nach dem deutschen Mathematiker Gottfried Wilhelm Leibniz.
Produktregel ableiten — 3 Faktoren
Besteht eine Funktion aus mehr als 2 Faktoren, nutzt du die erweiterte Formel der Produktregel. Für ein Produkt mit 3 Faktoren sieht die Produktregel so aus:
f(x) = u(x) • v(x) • w(x)
f’(x) = u’(x) • v(x) • w(x) + v’(x) • u(x) • w(x) + w’(x) • u(x) • v(x)
Um die Ableitung eines Produkts mit mehr als zwei Faktoren zu berechnen, musst du für jeden Faktor die Ableitung berechnen und diese dann mit den restlichen Faktoren multiplizieren. Anschließend addierst du alle diese Produkte zusammen.
Schau dir dazu das folgende Beispiel an:
f(x) = x2 • sin(x) • 5x
| u(x) = x2 | v(x) = sin(x) | w(x) = 5x |
| u'(x) = 2x | v‘(x) = cos(x) | w‘(x) = 5 |
f’(x) = 2x • sin(x) • 5x + cos(x) • x2 • 5x + 5 • x2 • sin(x)
Produktregel — häufigste Fragen
-
Wie kann man eine Funktion mit der Produktregel ableiten?
Mit der Produktregel leitest du Funktionen ab, die aus einem Produkt bestehen: (u • v)‘ = u‘ • v + u • v‘. Das heißt, du leitest die erste Funktion ab und multiplizierst sie mit der zweiten. Danach multiplizierst du die erste Funktion mit der Ableitung der zweiten und addierst beide Produkte.
-
Wie lautet die Produktregel Formel?
Um ein Produkt aus zwei Funktionen abzuleiten, nutzt du die Produktregel. Ihre Formel lautet: f‘ = u‘ • v + u • v‘.
-
Wie leite ich ein Produkt ab?
Die Produktregel brauchst du bei der Ableitung von Funktionen, die aus einem Produkt bestehen. Dafür zerlegst du deine Funktion f(x) in zwei Teilfunktionen u(x) und v(x). u und v kannst du mit den anderen Ableitungsregeln ableiten (u‘ und v‘) und in deine Produktregel einsetzen.
Quotientenregel Ableitung
Jetzt kannst du Produkte ableiten, aber wie gehst du mit gebrochen-rationalen Funktionen um? Bei Ableitungen von Funktionen mit Brüchen brauchst du die Quotientenregel.
![\[ f = \frac{\textcolor{blue}{u}}{\textcolor{red}{v}} \;\Longrightarrow\; f' = \frac{\textcolor{red}{v}\cdot\textcolor{blue}{u'} - \textcolor{red}{v'}\cdot\textcolor{blue}{u} }{ \textcolor{red}{v}^2 } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-587e16e2f1b149053d0170a1f05a0ec0_l3.png "Rendered by QuickLaTeX.com")
Schaue dir am besten unser Video dazu an!
Weitere Ableitungsregeln
Die Produktregel ist eine von vielen Ableitungsregeln der Differentialrechnung. Weitere wichtige Ableitungsregeln sind:
| Ableitungsregel | Funktion | Ableitung |
| Quotientenregel |  |
![f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-1128d60300515aa8b8df5c88d4dbbdf9_l3.png "Rendered by QuickLaTeX.com") |
| Summenregel |  |
 |
| Differenzregel |  |
 |
| Kettenregel |  |
 |
| Potenzregel |  |
 |
| Faktorregel |  |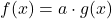
 |