Aufleiten
Du möchtest wissen, wie das Aufleiten funktioniert? Hier und im Video erklären wir dir einfach und verständlich, wie du Schritt für Schritt eine Funktion aufleitest.
Inhaltsübersicht
Aufleiten einfach erklärt
Beim Aufleiten berechnest du die Stammfunktion bzw. das Integral F(x) deiner Funktion. Deshalb sagst du zum Aufleiten eigentlich „integrieren“. Mithilfe der Aufleitung kannst du dann den Flächeninhalt unter deinem Funktionsgraphen bestimmen.
Das Aufleiten ist das genaue Gegenteil vom Ableiten. Denn mit der Aufleitung machst du die Rechnung der Ableitung rückgängig. So ist deine Stammfunktion F(x) abgeleitet die Funktion f(x). Wenn du f(x) hingegen aufleitest, erhältst du wieder F(x).
![Rendered by QuickLaTeX.com \[ F(x) = \int_0^x f(x)\mathop{\mathrm{d}x} \quad\Longleftrightarrow\quad F'(x) = f(x) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-34f0b2a370a17a9bca2fa800480290ae_l3.png)
Um aufzuleiten brauchst du dich nur an die Integrationsregeln zu halten. Die zeigen wir dir jetzt!
Konstanten aufleiten
Die einfachste Art der Aufleitung ist die Aufleitung von Konstanten. Um solche Konstanten aufzuleiten, multiplizierst du sie mit x und addierst dann ein C. C ist dabei die sogenannte Integrationskonstante und steht für eine beliebige Zahl.
f(x) = 3 → F(x) = 3x + C
f(x) = 5 → F(x) = 5x + C
Du brauchst das C, weil es für eine Aufleitung f(x) unendlich viele Stammfunktionen F(x) gibt. Sieh dir dafür folgendes Beispiel an.
F1(x) = 3x + 4 → f(x) = 3
F2(x) = 3x + 7 → f(x) = 3
Für f(x) = 3 kann die Stammfunktion sowohl F1(x) als auch F2(x) sein. Theoretisch könntest du also eine beliebige Zahl an deine Stammfunktion anhängen. Weil es damit aber unendlich viele richtige Lösungen geben würde, hängst du einfach die Konstante C an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Potenzregel
Die erste wichtige Regel ist die Potenzregel. Mit ihr leitest du Potenzfunktionen ab:
 ⋅ xn+1 + C
⋅ xn+1 + C
Das schauen wir uns genauer an dem Beispiel f(x) = x² an. Deine Hochzahl ist hier n = 2. Mehr brauchst du nicht, um alles in die Potenzregeln einzusetzen.
f(x) = x²
F(x) =  ⋅ x2+1 + C =
⋅ x2+1 + C = 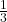 x³ + C
x³ + C
Faktorregel
Dann gibt es noch die Faktorregel. Hier ziehst du den Koeffizienten einer Funktion beim Aufleiten vor das Integral. Sieh dir dafür das Beispiel f(x) = 3x² an.
f(x) = 3x²
F(x) =  = 3 ⋅
= 3 ⋅  = 3 ⋅
= 3 ⋅  ⋅ x2+1 + C
⋅ x2+1 + C
F(x) = 3 ⋅ 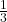 ⋅ x³ + C = x³ + C
⋅ x³ + C = x³ + C
Tipp: Die Faktorregel verwendest du oft in Kombination mit der Potenzregel. Deswegen verwendest du auch die gleiche Formel, nur dass du den Koeffizienten erst vor das Integral ziehst.
Summenregel
Die Summenregel vom Ableiten gibt es auch beim Aufleiten. Wenn du mehrere Summanden hast, darfst du sie einzeln integrieren. Schaue dir am besten ein paar Beispiele dazu an:
f(x) = 3x + 8x4
F(x) =  3x + 8x4
3x + 8x4
F(x) =  3x +
3x +  8x4
8x4
→ F(x) =  x² +
x² +  x5 + C
x5 + C
f(x) = 6x³ + 5x² + x
F(x) =  6x³ + 5x² + x
6x³ + 5x² + x
F(x) =  6x³ +
6x³ +  5x² +
5x² +  x
x
→ F(x) =  x4 +
x4 +  x³ +
x³ +  x² + C
x² + C
Beim Aufleiten gibt es für komplexere Funktionen, auch noch komplexere Integrationsregeln.
- Bei Funktionen, die aus Produkten von mehreren Teilfunktionen bestehen, verwendest du die partielle Integration. Wie du solche Funktionen aufleitest, zeigen wir dir hier.
- Bei gebrochen-rationalen oder anderen verketteten Funktionen wendest du die Integration durch Substitution an. Hier erklären wir dir genauer, wie das geht.
Aufleiten — häufigste Fragen
(ausklappen)
Aufleiten — häufigste Fragen
(ausklappen)-
Wie macht man eine Aufleitung?Beim Aufleiten suchst du eine Funktion, deren Ableitung die gegebene Funktion ergibt. Dazu verwendest du Regeln wie die Potenzregel, bei der du den Exponenten um 1 erhöhst und durch den neuen Exponenten teilst. Zusätzlich hängst du immer eine Konstante C hinten an.
-
Wie nennt man aufleiten?Das Aufleiten wird auch Integrieren genannt. Du bildest dabei die Stammfunktion einer gegebenen Funktion. In der Mathematik bezeichnest du das gesamte Verfahren als Integralrechnung.
Integralrechnung
Noch mehr Beispiele und Details zum Thema Integrale zeigen wir dir in unserem Video zur Integralrechnung!

