Was bringen mir Additionstheoreme bei Sinus, Cosinus und Tangens?

Additionstheoreme helfen dabei, , oder von einer Summe oder Differenz wie oder zu berechnen, wenn die Funktionswerte zu und bekannt sind. Konkret zerlegen sie Ausdrücke wie in Produkte aus Sinus- und Cosinuswerten.

Wie merke ich mir die Vorzeichen bei Sinus und Cosinus?

Die Vorzeichen folgen einem festen Muster: Beim Sinus bleibt das Vorzeichen in der Mitte gleich wie im Argument, beim Cosinus wechselt es. Konkret: , aber .

Wie leite ich das Additionstheorem für Sinus mit der Eulerformel her?

Das Additionstheorem für Sinus erhält man, indem und sowie und eingesetzt und ausmultipliziert werden. Zum Beispiel wird zu .

Wie leite ich das Additionstheorem für Cosinus mit Exponentialtermen her?

Das Additionstheorem für Cosinus entsteht, indem und (und entsprechend für ) eingesetzt und die Terme zusammengefasst werden. Beispiel: vereinfacht sich zu .

Wie leite ich das Additionstheorem für Tangens aus Sinus und Cosinus her?

Das Additionstheorem für Tangens folgt aus , indem Zähler und Nenner passend umgeschrieben und dann die Additionstheoreme für Sinus und Cosinus eingesetzt werden. Beispiel: und , daraus .

Video

Quiz

Additionstheoreme

Wichtige Inhalte in diesem Video

Additionstheoreme einfach erklärt

(00:12)

Additionstheoreme Beweis

(00:53)

Additionstheoreme Sinus

(00:53)

Additionstheoreme Cosinus

(01:56)

Der folgende Beitrag enthält eine Formelsammlung der Additionstheoreme von Sinus, Cosinus und Tangens, sowie deren Beweise.

Du möchtest möglichst schnell die Herleitung der Additionstheoreme verstehen? Dann schau dir am besten unser Video dazu an.

Inhaltsübersicht

Additionstheoreme einfach erklärt

im Videozur Stelle im Video springen

(00:12)

Additionstheoreme sind hilfreich, wenn man den Funktionswert einer trigonometrischen Funktion $\sin$ , $\cos$ oder $\tan$ von der Summe bzw. Differenz zweier Argumente berechnen möchte und den der einzelnen Argumente bereits kennt.

Additionstheoreme Sinus

$\sin(a+b) = \sin(a)\cdot \cos(b) + \cos(a) \cdot \sin(b)$

$\sin(a-b) = \sin(a)\cdot \cos(b) - \cos(a) \cdot \sin(b)$

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Additionstheoreme Cosinus

$\cos(a+b) = \cos(a)\cdot \cos(b) - \sin(a) \cdot \sin(b)$

$\cos(a-b) = \cos(a)\cdot \cos(b) + \sin(a) \cdot \sin(b)$

Additionstheoreme Tangens

$\tan(a+b) = \frac{\tan(a) + \tan(b)}{1-\tan(a) \cdot \tan(b)}$

$\tan(a-b) = \frac{\tan(a) - \tan(b)}{1+\tan(a) \cdot \tan(b)}$

Additionstheoreme Beweis

im Videozur Stelle im Video springen

(00:53)

Für die Herleitung der Additionstheoreme verwenden wir die folgende Charakterisierung von Sinus und Cosinus, welche sich aus der Eulerformel ergibt

$\sin(a) = \frac{1}{2i} \left(e^{ia}-e^{-ia}\rigt)$

$\cos(a) = \frac{1}{2} \left(e^{ia}+e^{-ia}\rigt).$

Additionstheoreme Sinus

im Videozur Stelle im Video springen

(00:53)

Wir wollen zeigen, dass gilt

$\sin(a\pm b) = \sin(a)\cdot \cos(b) \pm \cos(a) \cdot \sin(b)$ .

Dafür betrachten wir

$\sin(a)\cdot \cos(b) = \frac{1}{2i} \left(e^{ia}-e^{-ia}\rigt) \cdot \frac{1}{2} \left(e^{ib}+e^{-ib}\rigt)$

$=\frac{1}{4i}\left(e^{i(a+b)} +e^{i(a-b)}-e^{-i(a-b)} - e^{-i(a+b)}\right)$

und

$\cos(a)\cdot \sin(b) = \frac{1}{2} \left(e^{ia}+e^{-ia}\rigt) \cdot \frac{1}{2i} \left(e^{ib}-e^{-ib}\rigt)$

$= \frac{1}{4i} \left( e^{i(a+b)} - e^{i(a-b)} + e^{-i(a-b)} - e^{-i(a+b)}\right)$ .

Berechnen wir die Summe der beiden Terme, ergibt sich

$\sin(a)\cdot \cos(b) + \cos(a)\cdot \sin(b) = \frac{1}{4i}\left(2e^{i(a+b)}- 2e^{-i(a+b)}\right)$

$= \frac{1}{2i}\left(e^{i(a+b)}-e^{-i(a+b)}\right)$

$=\sin(a+b)$ .

Analog können wir die Differenz der Terme berechnen und erhalten

$\sin(a)\cdot \cos(b) - \cos(a)\cdot \sin(b) = \frac{1}{4i}\left( 2e^{i(a-b)} -2e^{-i(a-b)}\right)$

$= \frac{1}{2i}\left(e^{i(a-b)} -e^{-i(a-b)}\right)$

$=\sin(a-b)$ .

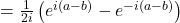
Damit sind die Theoreme für die Sinus Funktion gezeigt.

Additionstheoreme — häufigste Fragen

(ausklappen)

Was bringen mir Additionstheoreme bei Sinus, Cosinus und Tangens?

Additionstheoreme helfen dabei, $\sin$ , $\cos$ oder $\tan$ von einer Summe oder Differenz wie oder zu berechnen, wenn die Funktionswerte zu und bekannt sind. Konkret zerlegen sie Ausdrücke wie $\sin(a+b)$ in Produkte aus Sinus- und Cosinuswerten.
Wie merke ich mir die Vorzeichen bei Sinus und Cosinus?

Die Vorzeichen folgen einem festen Muster: Beim Sinus bleibt das Vorzeichen in der Mitte gleich wie im Argument, beim Cosinus wechselt es. Konkret: $\sin(a-b)=\sin(a)\cos(b)-\cos(a)\sin(b)$ , aber $\cos(a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)$ .
Wie leite ich das Additionstheorem für Sinus mit der Eulerformel her?

Das Additionstheorem für Sinus erhält man, indem $\sin(a)=\frac{1}{2i}(e^{ia}-e^{-ia})$ und $\cos(b)=\frac{1}{2}(e^{ib}+e^{-ib})$ sowie $\cos(a)$ und $\sin(b)$ eingesetzt und ausmultipliziert werden. Zum Beispiel wird $\sin(a)\cos(b)+\cos(a)\sin(b)$ zu $\frac{1}{2i}(e^{i(a+b)}-e^{-i(a+b)})=\sin(a+b)$ .
Wie leite ich das Additionstheorem für Cosinus mit Exponentialtermen her?

Das Additionstheorem für Cosinus entsteht, indem $\cos(a)=\frac{1}{2}(e^{ia}+e^{-ia})$ und $\sin(a)=\frac{1}{2i}(e^{ia}-e^{-ia})$ (und entsprechend für ) eingesetzt und die Terme zusammengefasst werden. Beispiel: $\cos(a)\cos(b)-\sin(a)\sin(b)$ vereinfacht sich zu $\frac{1}{2}(e^{i(a+b)}+e^{-i(a+b)})=\cos(a+b)$ .
Wie leite ich das Additionstheorem für Tangens aus Sinus und Cosinus her?

Das Additionstheorem für Tangens folgt aus $\tan(x)=\frac{\sin(x)}{\cos(x)}$ , indem Zähler und Nenner passend umgeschrieben und dann die Additionstheoreme für Sinus und Cosinus eingesetzt werden. Beispiel: $\tan(a)+\tan(b)=\frac{\sin(a)\cos(b)+\sin(b)\cos(a)}{\cos(a)\cos(b)}=\frac{\sin(a+b)}{\cos(a)\cos(b)}$ und $1-\tan(a)\tan(b)=\frac{\cos(a+b)}{\cos(a)\cos(b)}$ , daraus $\tan(a+b)=\frac{\tan(a)+\tan(b)}{1-\tan(a)\tan(b)}$ .