Video anzeigen

Hier geht's zum Video „Radius berechnen“

Hier geht's zum Video „Durchmesser berechnen“

Hier geht's zum Video „Tangente“

Hier geht's zum Video „Kreisbogen und Kreisausschnitt“

Hier geht's zum Video „Kreisbogen und Kreisausschnitt (Kreisausschnitt)“

Hier geht's zum Video „Kreisberechnung“

Kreis

Wichtige Inhalte in diesem Video

Kreis Definition

Mittelpunkt, Radius, Durchmesser und Kreislinie

Wichtige Begriffe im Kreis

Kreis und Geraden

Du willst alles Wichtige über den Kreis erfahren? Dann bist du hier und in unserem Video genau richtig!

Inhaltsübersicht

Kreis Definition

im Videozur Stelle im Video springen

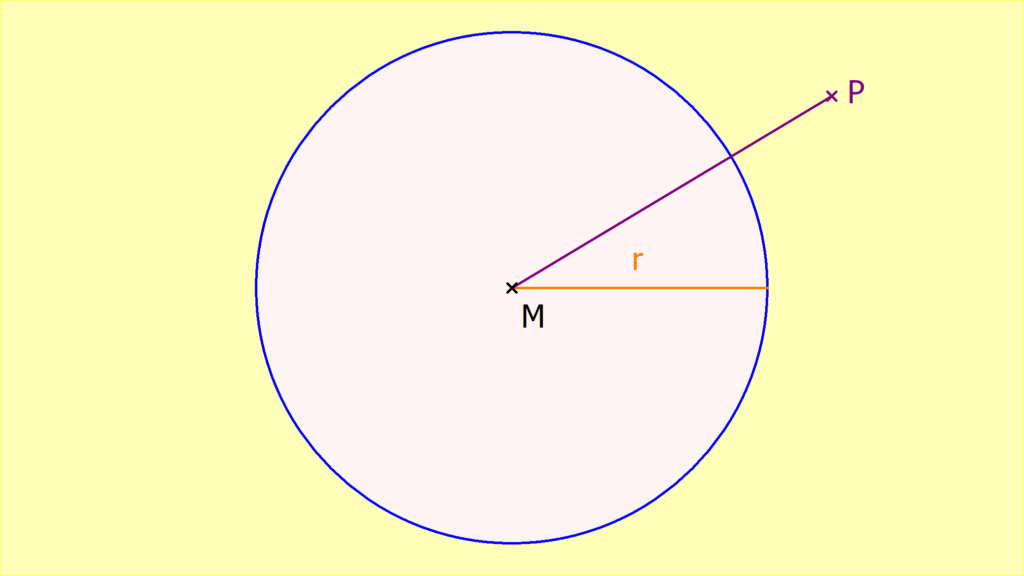
Der Kreis gehört zu den geometrischen Figuren . Er ist komplett rund und wird durch eine Kreislinie abgeschlossen. Alle Punkte auf dieser Kreislinie sind gleich weit vom Mittelpunkt M entfernt. Den Abstand vom Mittelpunkt M zu jedem Punkt auf der Kreislinie nennst du auch Radius r.

Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis — Kreis mit Mittelpunkt und Radius

Es gibt ein paar wichtige Kreis Begriffe, die du kennen solltest. Schau sie dir jetzt an!

Mittelpunkt, Radius, Durchmesser und Kreislinie

im Videozur Stelle im Video springen

Mittelpunkt

Der Mittelpunkt M liegt in der Mitte des Kreises. Alle Punkte auf der Kreislinie haben den gleichen Abstand zu ihm.

Radius

Der Radius r ist der Abstand von einem Punkt der Kreislinie zum Mittelpunkt M. Er beschreibt nicht nur eine Länge, sondern auch eine Strecke vom Mittelpunkt M zu einem anderen Punkt auf der Kreislinie.

Durchmesser

Der Durchmesser d ist der größtmögliche Abstand von zwei Punkten der Kreislinie. Die Punkte liegen dabei genau gegenüber voneinander. Der Durchmesser verläuft immer durch den Mittelpunkt M. Auch er beschreibt nicht nur eine Länge, sondern auch eine Strecke.

Kreis Durchmesser, Durchmesser im Kreis, Was ist ein Durchmesser, Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis — Kreis mit Durchmesser und Radius

Radius und Durchmesser

Der Durchmesser d ist doppelt so lang wie der Radius r:

d = 2 · r

Der Radius r ist halb so lang wie der Durchmesser d:

r = ½ · d

Kreis Durchmesser, Durchmesser im Kreis, Was ist ein Durchmesser, Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis — Kreis mit Radius und Durchmesser

Wichtige Begriffe im Kreis

im Videozur Stelle im Video springen

Andere Begriffe zum Kreis, wie Kreisinneres und -äußeres zeigen wir dir hier. Auch besondere Punkte und Geraden im Kreis solltest du kennen.

Kreisinneres und Kreisäußeres

Das Kreisinnere bezeichnet die Fläche innerhalb der Kreislinie. Der Abstand von Punkten im Kreisinneren zum Mittelpunkt ( $\overline{MP}$ ) ist also immer kleiner als der Radius r.

$\overline{MP}$ < r

Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis, Kreisinneres — Kreisinneres

Das Kreisäußere bezeichnet die Fläche außerhalb der Kreislinie. Der Abstand von Punkten im Kreisäußeren zum Mittelpunkt ist immer größer als der Radius r.

$\overline{MP}$ > r

Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis, Kreisäußeres — Kreisäußeres

Kreis und Punkte

Es gibt ein paar wichtige Punkte am Kreis, die wir dir hier vorstellen:

Randpunkt

Alle Punkte, die auf der Kreislinie liegen, sind Randpunkte. Es gilt

$\overline{MP}$ = r

Mathematisch kannst du die Randpunkte so schreiben: P ∈ k(M;r), also Punkt P ist ein Element von der Kreislinie.

Innerer Punkt Kreis, Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis — Kreis Randpunkt

Innerer Punkt

Alle Punkte im Kreisinneren nennst du innere Punkte. Es gilt

$\overline{MP}$ < r

Innerer Punkt Kreis, Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis — Kreis Innerer Punkt

Äußerer Punkt

Alle Punkte im Kreisäußeren nennst du äußere Punkte. Es gilt

$\overline{MP}$ > r

Innerer Punkt Kreis, Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis — Kreis Äußerer Punkt

Kreis und Geraden

im Videozur Stelle im Video springen

Vielleicht kennst du auch die Begriffe Passante, Sekante und Tangente. Was es damit auf sich hat, siehst du hier:

Geraden am Kreis, Passante, Tangente, Sekante — Geraden am Kreis

Eine Gerade, die den Kreis

in keinem Punkt berührt, nennst du Passante.
in einem Punkt berührt, nennst du Tangente .
in zwei Punkten schneidet, nennst du Sekante .

Übrigens:

Eine Sekante, die durch den Mittelpunkt verläuft, nennst du Zentrale.
Den Teil einer Sekante, der im Kreisinneren liegt, nennst du Sehne. (Die längste Sehne ist der Durchmesser d)

Kreis Formeln

Für einige Kreis Formeln brauchst du die Kreiszahl π (Pi). Gerundet ist π ≈ 3,14.

Hier hast du einen Überblick über alle wichtigen Kreisformeln :

Radius r = ½ · d
Durchmesser d = 2 · r
Umfang U = 2π · r
Flächeninhalt A = π · r²

Kreisteile

Einzelne Teile des Kreises haben eigene Bezeichnungen. Hier siehst du sie:

Kreisbogen und Kreisausschnitt

im Videozur Stelle im Video springen

Der Kreisbogen b ist ein Teil der Kreislinie. Die Kreisbogenlänge b hängt von dem Winkel α ab. Du berechnest ihn mit der Formel:

$\textcolor{red}{b} =\frac{\textcolor{orange}{\alpha}}{360^\circ} \cdot 2 \cdot \pi \cdot \textcolor{blue}{r}$

Der Kreisausschnitt oder Kreissektor A_s ist ein Teil des Flächeninhalts eines Kreises. Der Kreisausschnitt hängt vom Winkel α ab. Du berechnest ihn mit der Formel

$\textcolor{violet}{A_S} =\frac{\textcolor{orange}{\alpha}}{360^\circ} \cdot \pi \cdot \textcolor{blue}{r}^2$ .

Kreis, Winkel, Bogen, Radius, Durchmesser — Kreisbogen und Kreisausschnitt

Kreisring

Der Kreisring ist die Fläche, die einen Kreis mit großem Radius r_g und einen Kreis mit kleinem Radius r_k einschließt. Sie haben denselben Mittelpunkt M.

Ein Kreis, Kreislinie, Kreis Definition, Was bedeutet das r im Kreis, Kreis Mathe, Definition Kreis, Was ist ein Kreis, Kreis Geometrie, Geomtrie Kreis, Kreis Begriffe, Kreis Mathematik, Kreis mit Punkt in der Mitte, Mittelpunkt Kreis, Eigenschaften Kreis, Mathe Kreis, Kreisring — Kreisring

Kugel

Ein Kreis im dreidimensionalen Raum ist eine Kugel . In unserem Video erfährst du alles Wichtige dazu!

Zum Video: Oberfläche Kugel

Beliebte Inhalte aus dem Bereich Geometrie

Kreis berechnen

Kreisberechnung

Radius berechnen

Durchmesser berechnen

Flächeninhalt Kreis

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .